Commentaires sur le §13 de l’Analysis Situs (Équivalences fondamentales)

Lorsque l’on peut voir une variété comme le quotient $Y/G$ d’un espace simplement connexe $Y$ par un sous-groupe $G$ de difféomorphismes de $Y$ opérant proprement et librement alors $G$, comme groupe de monodromie du revêtement universel $Y \to Y/G$, est aussi le groupe fondamental de $Y/G$. [1]

Cette méthode s’applique en particulier aux variétés du §11 (et donc en particulier aux exemples 1 et 4 du § 10) et aussi à l’exemple 5 du §10, qui est visiblement difféomorphe au quotient $\mathbb{S}^3 / \{ \pm 1 \}$. Ici $-1$ désigne l’application antipodie de l’hypersphère, qui envoie chaque point de $\mathbb{S}^3$ en celui qui est diamétralement opposé.

Pour calculer les groupes fondamentaux des autres exemples du §10, Poincaré propose une méthode qui s’applique à toutes les variétés polyédriques $P/\iota$ comme dans §10 (et nos commentaires sur ce dernier) [2]. Nous résumons la méthode de Poincaré dans la proposition suivante.

Le groupe $G$ est donc donné par générateurs et relations. En passant à l’abélianisé on obtient (le premier groupe d’homologie et donc) le premier nombre de Betti. Si $W$ est une variété orientable, la dualité de Poincaré (que Poincaré « démontre » au §9, voir nos commentaires) identifie ce dernier au nombre de Betti de codimension 1. La méthode ci-dessus permet donc de calculer tous les nombres de Betti de n’importe quelle variété de dimension $\leq 3$.

Démonstration. 1. Toute classe d’équivalence de lacet contient un lacet en position générale relativement aux faces. Un tel lacet rencontre les faces de codimension 1 transversalement en des points isolés dans l’intérieur de ces faces, on peut donc le décomposer comme le montre le dessin ci-dessous en une somme de lacets du type $\pm \mathcal{F}$.

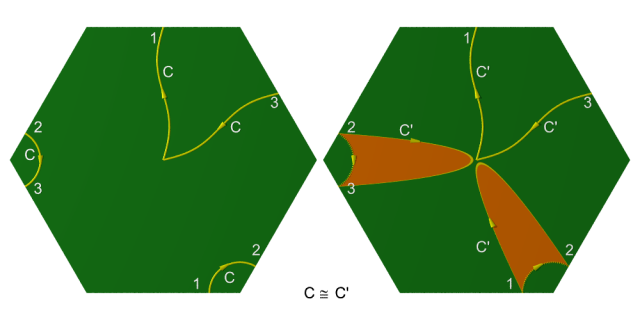
2. Le fait que les équivalences fondamentales soient bien des équivalences découle de ce que $\mathcal{F}_i \equiv p v_{i-1} v_i p$, les $v_i$ étant les sommets consécutifs du link (polygonal) de la cellule de codimension 2 correspondante dans le quotient $P/\iota$. [4]

Finalement, toute équivalence entre nos lacets est déterminée par une application d’un 2-disque dans $W$. On peut toujours supposer que cette application est en position générale, de sorte qu’elle intersecte les cellules de codimension 2 de $P/\iota$ transversalement en des points isolés. L’équivalence associée peut alors s’écrire comme la somme des équivalences fondamentales associées à ces points.

C.Q.F.D.

$$ $$

Besoin de plus de détails ?

On donne ici une énoncé plus formel et deux démonstrations de ce résultats. La seconde via le théorème de Van Kampen est essentiellement ce que suggère Poincaré. La première consiste à identifier le revêtement universel et à voir le groupe fondamental comme groupe de monodromie, elle suit la démonstration de son théorème du domaine fondamental, qu’il a développée dans sa théorie des groupes fuchsiens. Il y a peu de doutes que Poincaré avait également cette image en tête.

$$ $$

Application au calcul du groupe fondamental des surfaces

Considérons une surface de genre $g$ vue comme le quotient d’un $4g$-gone $P$ par l’identification $\iota$ représentée sur l’image suivante :

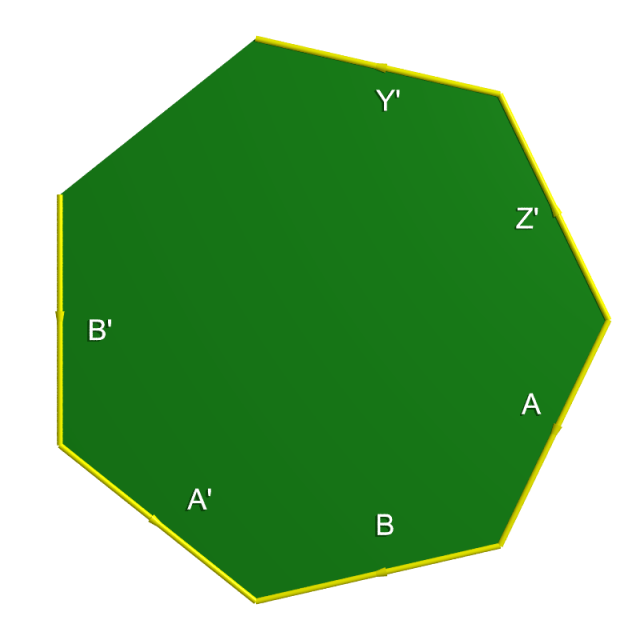
Le quotient $P/\iota$ ne possède qu’une unique cellule de codimension 2, à savoir la classe de tous les sommets de $P$ :

$$\{ Z' \cap A , A' \cap B' , B \cap A' , A \cap B , \ldots \}.$$

Le groupe fondamental $G$ est engendré par les lacets $\{ \mathcal{A} , \mathcal{B} , \ldots \}$ soumis à la relation :

$$\mathcal{A} - \mathcal{B} - \mathcal{A} + \mathcal{B} + \mathcal{C} - \ldots \equiv 0 .$$

Ainsi pour $g\geq 2$ le groupe fondamental de la surface est non-abélien. De plus, l’abélianisé de la relation ci-dessus se réduit à $0 \sim 0$, de sorte que le premier groupe d’homologie de la surface est une groupe libre abélien engendré par les $2g$ générateurs $\{\mathcal{A} , \mathcal{B} , \ldots \}$. Donc $b_1 = 2g$.

$$ $$

Poincaré applique en particulier sa méthode à la variété de l’exemple 3 du §10 [5] :

La démonstration de cette proposition est reprise ici. Notons que Poincaré identifie le groupe

$$\langle i , j , k \; | \; k=ij , \ i=jk, \ j=ki , \ ikj=1 \rangle$$

au groupe [6]

$$\langle i, j , k \; | \; i^2 = j^2 = k^2 , \ k=ij , \ i^4 = 1 \rangle$$

dont on peut facilement vérifier qu’il est isomorphe au groupe d’ordre 8 des quaternions unitaires situés sur les axes de coordonnées de $\mathbb{R}^4$.

$$ $$

Envie de voir les calculs ?

Considérons le groupe $G$ défini par la présentation $\langle i , j , k \; | \; k=ij , \ i=jk, \ j=ki , \ ikj=1 \rangle$. Les $4$ relations permettent d’exprimer $k$ de $4$ manières différentes comme produit de $i^{\pm 1}$ et $j^{\pm 1}$ : $k =ij = j^{-1} i = j i^{-1} = i^{-1} j^{-1}$. L’égalité $ij = i^{-1} j^{-1}$ implique $j^2 = i^{-2}$ et l’égalité $ j^{-1} i = j i^{-1}$ implique $i^2 = j^2$. En combinant ces deux égalités de puissances deuxièmes, on déduit que $i^2 = j^2$ et que $i^4 =1$. Il nous reste à prouver que $k^2= i^2$. Cela s’obtient en multipliant les égalités $k= ij$ et $k = j^{-1}i$, dans cet ordre.

Tout élément du groupe $G$ peut alors s’écrire de manière unique sous la forme $i^a j^b$ avec $0\leq a \leq 3$ et $0 \leq b \leq 1$ : on peut en effet remplacer $k$ par $ij$, puis chaque $ji$ par $i^3 j^3$ pour obtenir $i^a j^b$. Puisque $i$ et $j$ sont d’ordre $4$, on peut clairement prendre $0 \leq a , b \leq 3$ ; on peut de plus remplacer $j^2$ par $i^2$ et $j^3$ par $i^2 j$, de sorte que l’on peut prendre $0 \leq b \leq 1$. Cela signifie que $G$ a au plus $8$ éléments.

Comme le sous-groupe $G'$ du groupe multiplicatif des quaternions unitaires engendré par les quaternions de base $i, j, k$ vérifie les relations de présentation de $G$, il s’agit d’un quotient de ce dernier. Mais $G'$ a exactement $8$ éléments, ce qui montre que $G$ a aussi $8$ éléments et que les deux groupes sont isomorphes.

$$ $$

Les homologies fondamentales sont

$$2X \sim 2Y \sim 2Z , \quad 4X \sim 0$$

ce qui implique que le premier groupe d’homologie de la variété construite dans l’exemple 3 du §10 est le groupe abélien engendré par $X$ et $Y$ et soumis aux relations [7]

$$2X \sim 0 \mbox{ et } 2Y\sim 0.$$

Ce groupe est donc isomorphe à $\mathbb{Z}/2\mathbb{Z} \oplus \mathbb{Z}/2\mathbb{Z}$, ce qui montre que les nombres de Betti en dimensions $1$ et $2$ de cette variété de dimension $3$ sont $b_1=b_2=0$. Notons que l’hypersphère $\mathbb{S}^3$ et l’espace projectif réel $\mathbb{RP}^3$ ont les mêmes nombres de Betti ; néanmoins les groupes d’homologie de ces trois variétés sont distincts.

$$ $$

Lacets ou monodromie ?

On peut remarquer qu’identifier la variété construite dans l’exemple 3 du §10 au quotient de l’hypersphère $\mathbb{S}^3$ par le groupe $Q_8$ de quaternions --- comme le fait Poincaré juste après --- permet d’éviter d’identifier le groupe

$$\langle i , j , k \; | \; k=ij , \ i=jk, \ j=ki , \ ikj=1 \rangle$$

donné par générateurs et relations, ce qui peut s’avérer délicat en général. Néanmoins, Poincaré pousse ici jusqu’au bout le calcul du groupe fondamental via les générateurs et les relations. Il en fait d’ailleurs de même dans les exemples 1, 4 et 5, alors qu’eux aussi peuvent immédiatement être obtenus comme quotient $Y/G$ avec $Y$ simplement connexe. L’explication est certainement que Poincaré veut mettre ici en avant sa deuxième approche pour le calcul du groupe fondamental et cherche à convaincre le lecteur que l’on peut tout calculer via les lacets sans avoir à passer au revêtement universel. Ceci est à contraster avec sa Note de 1892, dans laquelle il avait pour la première fois introduit le groupe fondamental.

$$ $$

L’hypersphère comme groupe de Lie

La multiplication des quaternions munit l’hypersphère $\mathbb{S}^3$ d’une structure de groupe de Lie isomorphe au groupe $\mathrm{SU} (2)$ via l’application

$$x+iy+jz+kt \to \left( \begin{array}{cc} x+iy & z+it \\ -z+it & x-iy \end{array} \right).$$

Si l’on pense au groupe fondamental de la variété hypercubique comme au sous-groupe engendré par $i$, $j$ et $k$, alors la variété hypercubique est la variété homogène obtenue en quotientant $\mathbb{S}^3$ par ce sous-groupe. De même, la variété dodécaédrique que Poincaré construit d’une autre manière au cinquième complément peut s’obtenir comme quotient de $\mathbb{S}^3$ par un (autre) sous-groupe fini à 120 éléments, le groupe des icosions, dont l’abénialisé est trivial. La variété dodécaédrique a donc les même groupes d’homologie que l’hypersphère $\mathbb{S}^3$, on dit que c’est une sphère d’homologie. Il est (presque) étrange que Poincaré « loupe » cette construction. La construction de cette même sphère d’homologie qu’il finira par donner dans le cinquième complément est très différente. On en donne plusieurs constructions équivalentes ici.

$$ $$

En particulier, pour l’exemple 1 on a $\: b_1=b_2 = 3$, alors que pour l’exemple 4, on a $\: b_1=b_2 = 1$. L’étude des différents recollements du cube est détaillée ici.

Démonstration. Soit $T=\left( \begin{smallmatrix} a & b \\ c & d \end{smallmatrix} \right) \in \mathrm{SL} (2, \mathbb{Z})$. Les trois générateurs du groupe correspondant $G_T$ sont

$$C_1 : (x,y,z) \mapsto (x+1 , y , z ), $$

$$C_2 : (x,y,z) \mapsto (x, y+1 , z) $$

et

$$C_3 : (x,y,z) \mapsto (ax+by , cx+ dy , z+1).$$

On a les relations suivantes entre ces trois générateurs :

$$C_1 + C_2 \equiv C_2 + C_1,$$

$$C_1 +C_3 \equiv C_3 + a C_1 + c C_2, $$

$$C_2 + C_3 \equiv C_3 + b C_1 + d C_2.$$

On affirme que le groupe fondamental $G=G_T$ de $\mathbb{R}^3 /G$ est isomorphe au groupe engendré par $C_1$, $C_2$ et $C_3$ soumis aux trois relations ci-dessus. [8]

En effet, les relations ci-dessus sont vérifiés dans $G_T$ et toute relation dans $G_T$ se ramène — via les trois relations ci-dessus — à une relation de la forme $m_1 C_1 + m_2 C_2 + m_3 C_3 \equiv 0$. Mais il est facile de vérifier que la transformation $m_1 C_1 + m_2 C_2 + m_3 C_3$ opère trivialement sur $\mathbb{R}^3$ si et seulement si les trois entiers $m_1$, $m_2$ et $m_3$ sont nuls. La relation devient donc la relation triviale $0 \equiv 0$.

En abélianisant les équivalences ci-dessus on obtient la relation trivial $0 \sim 0$ et les deux relations :

$$(a-1) C_1 + c C_2 \sim 0, $$

$$b C_1 + (d-1) C_2 \sim 0.$$

Le premier groupe d’homologie de la variété $\mathbb{R}^3 /G$ est donc le groupe abélien engendré par $C_1$, $C_2$ et $C_3$ soumis aux deux relations ci-dessus.

Mais les deux relations ci-dessus sont triviales si et seulement si $T=\mathrm{Id}$, de sorte que dans ce cas, et dans ce cas seulement, le premier groupe d’homologie est libre sur 3 générateurs et $b_1=b_2 =3$.

Si $T\neq \mathrm{Id}$, les relations ci-dessus sont équivalentes si et seulement si le déterminant $\left| \begin{smallmatrix} a-1 & b \\ c & d-1 \end{smallmatrix} \right|$ est nul, c’est-à-dire si et seulement si $\mathrm{trace} \ T = a+d=2$. De sorte que dans ce dernier cas, et dans ce dernier cas seulement, les nombres de Betti sont $b_1=b_2=2$.

Dans tous les autres cas les relations d’homologies sont non-triviales et non équivalentes et on a $b_1=b_2=1$.

C.Q.F.D.

$$ $$

Envie d’en savoir un peu plus ?

On peut calculer le premier groupe d’homologie (dont la structure détermine par dualité de Poincaré aussi celle du second) de la variété $\mathbb{R}^3 /G_T$. Ce groupe est isomorphe à $\mathbb{Z} \oplus \mathbb{Z} / s \mathbb{Z} \oplus \mathbb{Z} / t \mathbb{Z}$, où $s | t$, $s,t \geq 0$ sont les diviseurs élémentaires de la matrice $\left( \begin{smallmatrix} a-1 & b \\ c & d-1 \end{smallmatrix} \right)$ que l’on obtient en diagonalisant cette matrice à l’aide d’opérations élémentaires sur les lignes et les colonnes sur $\mathbb{Z}$. On a donc :

$$s = \mathrm{pgcd} (a-1 , c, b , d-1) \mbox{ et } st = \pm \left| \begin{smallmatrix} a-1 & b \\ c & d-1 \end{smallmatrix} \right|.$$

Cela montre en particulier que la variété de l’exemple 4, c’est-à-dire la variété $\mathbb{R}^3 / G_T$ avec $T = \left( \begin{smallmatrix} 0 & 1 \\ -1 & 0 \end{smallmatrix} \right)$ a les mêmes groupes d’homologie que la variété $\mathbb{R}^3 / G_{T'}$ avec $T' = \left( \begin{smallmatrix} 2 & 1 \\ 3 & 2 \end{smallmatrix} \right)$. Poincaré montre pourtant au paragraphe suivant (cf. nos commentaires) que ces deux variétés ne sont pas difféomorphes, en montrant que leurs groupes fondamentaux ne sont pas isomorphes.