Commentaires sur le §6 de l’Analysis Situs (Nombres de Betti)

Dans le §6, Poincaré définit ce qu’il appelle « les nombres de Betti » d’une variété.

Nous dirons que les variétés

$$v_1,v_2,…,v_\lambda,$$

d’un même nombre de dimensions et faisant partie de $V$, sont linéairement indépendantes, si elles ne sont liées par aucune homologie à coefficients entiers.

S’il existe $P_m-1$ variétés fermées à $m$ dimensions faisant partie de $V$ et linéairement indépendantes et s’il n’en existe que $P_m-1$, nous dirons que l’ordre de connexion de $V$ par rapport aux variétés à $m$ dimensions est égal à $P_m$.

Ainsi se trouvent définis, en ce qui concerne une variété $V$ à $m$ dimensions, $m−1$ nombres que j’appellerai

$$P_1,P_2,…,P_{m−1}$$

et qui sont les ordres de connexion de $V$ par rapport aux variétés de

$$1,2,…,m−1$$

dimensions.

Je les appellerai dans la suite les nombres de Betti.

Autrement dit, si $V$ est une variété à $m$ dimensions, pour $1\leq i\leq m-1$, on note $P_i$ le plus grand entier $p$ tel qu’on peut trouver $p−1$ sous-variétés fermées $v_1,…,v_{p−1}$ de dimensions $i$ dans $V$ qui ne sont liées par aucune homologie.

Les entiers $P_1,…,P_{m−1}$ sont les « nombres de connexions » ou « nombres de Betti » de la variété $V$.

Cette définition est d’une simplicité séduisante. Elle est en tout cas d’un accès beaucoup plus immédiat que celles qu’on peut trouver dans les livres modernes de topologie algébrique, où le $i$-ième nombre de Betti d’une variété $V$ est défini comme le rang du plus grand sous-module libre d’un module obtenu comme quotient du noyau d’un morphisme par l’image d’un autre... De plus, il nous semble que la définition de Poincaré résume parfaitement l’image mentale informelle qu’ont de nombreux mathématiciens contemporains : on mesure la « complexité » d’une variété $V$ en cherchant à « faire rentrer » dans $V$ un maximum de variétés fermées de dimension $i$, sans que leur union ne borde une variété de dimension $i+1$. Nous allons voir que la définition de Poincaré recèle hélas un certain nombre d’implicites, et que son sens précis est assez délicat à cerner [1].

Une définition difficile à appréhender.

La définition des nombres de Betti présuppose la notion d’« homologie », qui elle-même présuppose la notion de « frontière complète ». Nous avons vu dans les commentaires du §1 et du §5 les problèmes posés par les définitions de ces notions. Pour résoudre ces problèmes, nous supposerons, comme dans les commentaires du §5, que « variété à $i$ dimensions dans $V$ » signifie « sous-variété polyédrale de $V$ de dimension $i$ » (voir la définition dans les commentaires du §1). La « frontière complète » d’une variété à $i$ dimensions est alors bien définie. Il s’agit d’une union de variétés à $i-1$ dimensions deux à deux disjointes.

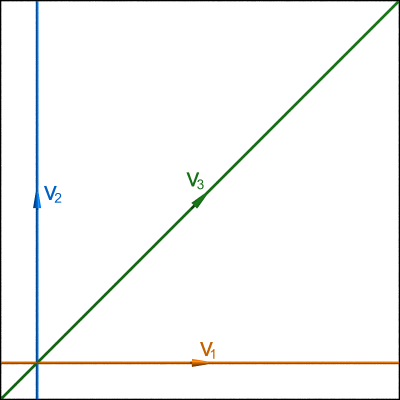
Essayons maintenant, en suivant scrupuleusement la définition de Poincaré, de trouver le nombre de Betti $P_1$ du tore $\mathbb{T}^2=\mathbb{R}^2/\mathbb{Z}^2$. Pour ce faire, nous devons considérer des courbes fermées orientées $v_1,\dots,v_p$ dans $\mathbb{T}^2$, et nous demander si ces courbes sont « liées par une homologie ». Considérons par exemple les courbes $v_1,v_2,v_3$ représentées sur le dessin ci-dessous.

Au premier abord, ces courbes semblent n’être reliées par aucune homologie (au sens défini par Poincaré). En effet, la frontière complète d’une « variété à deux dimensions dans $\mathbb{T}^2$ » est constituée de variétés à une dimension (i.e. d’arcs ouverts et de courbes fermées simples) deux à deux disjointes. Puisque les courbes $v_1,v_2,v_3$ s’intersectent deux à deux, il ne peut exister aucune variété à deux dimensions dans $\mathbb{T}^2$ dont le bord contienne deux des trois variétés $v_1,v_2,v_3$. On vérifie par ailleurs facilement qu’il n’existe aucune variété à deux dimensions dans $\mathbb{T}^2$ dont la frontière complète soit constituée de copies d’une seule des variétés $v_1,v_2,v_3$. Remplacer chaque $v_i$ par une variété fermée « peu différente » de $v_i$ (c’est-à-dire isotope à $v_i$) ne change rien au problème. On est donc tenté d’en déduire que, suivant la définition de Poincaré, le nombre de Betti $P_1$ du tore $\mathbb{T}^2$ est strictement supérieur à $3$. [2]

Mais c’est oublier un détail : Poincaré a précisé que les « homologies peuvent se combiner comme des équations ». La phrase « $v_1,v_2,v_3$ sont liées par une homologie » doit donc être interprétée, de manière à prendre en compte la possibilité de telles combinaisons. Elle ne signifie pas nécessairement qu’il existe une variété à deux dimensions dont la frontière est constituée de copies de $v_1,v_2,v_3$. On peut avoir une somme formelle de variétés à deux dimensions telle que la somme formelle des frontières de ces variétés est après simplification constituée de copies de $v_1,v_2,v_3$. Et c’est exactement ce qui arrive !

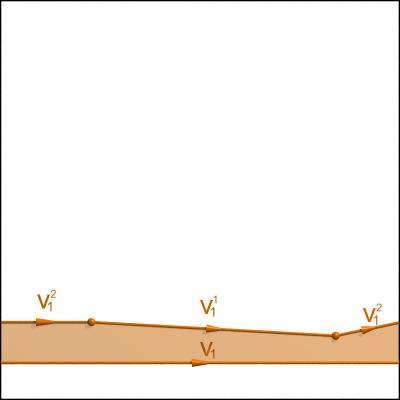
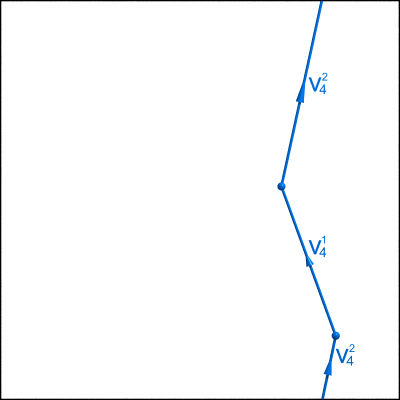
Pour $i=1,2,3$, on peut trouver un domaine à bord et coins de $\mathbb{T}^2$ dont le bord est formé de la courbe fermée $v_i$ et de deux arcs ouverts $v_i^1$ et $v_i^2$ ayant les mêmes extrémités (voir la figure ci-dessous). On a donc

$$v_i\sim v_i^1+v_i^2 \quad\quad i=1,2,3$$

Ce point est extrêmement important : à homologie près, on peut remplacer la courbe fermée $v_i$ par la somme de deux arcs ouverts. Ceci signifie que, du point de vue de l’homologie, on peut « subdiviser » les courbes fermées en sous-arcs. De même, on pourrait « subdiviser » les variétés de dimension $i$.

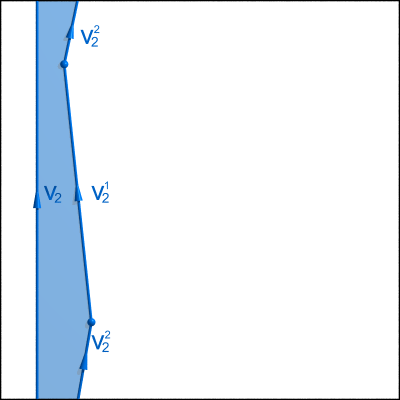
Rappelons que c’est l’existence d’intersections entre les courbes $v_1,v_2,v_3$ qui nous gênait pour trouver une homologie reliant ces courbes (car la frontière complète d’une variété à deux dimensions ne peut contenir deux courbes fermées qui s’intersectent). Mais le problème disparaît dès lors qu’on a remplacé (à homologie près) les courbes $v_1,v_2,v_3$ par des arcs ouverts qui ne s’intersectent pas. Il est alors facile de trouver une homologie reliant ces arcs. Pour ce faire, considérons deux autres arcs ouverts à extrémités communes $v_4^1,v_4^2$ comme ci-dessous :

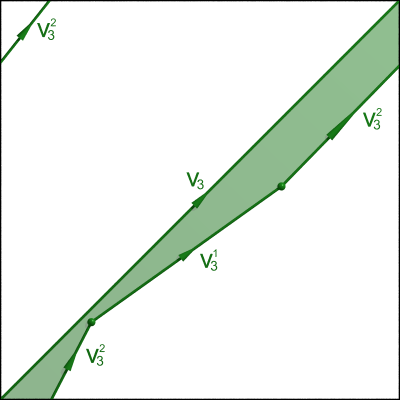
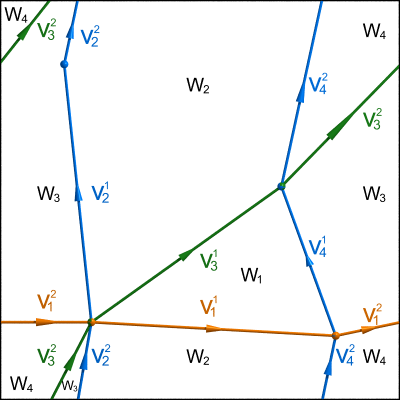
On constate que les arcs $v_i^j$ (pour $i=1,\dots,4$ et $j=1,2$) découpent le tore $T^2$ en quatre domaines $W_1,\dots,W_4$ :

Les frontières de ces domaines nous donnent les homologies suivantes :

$$\begin{eqnarray*} v_1^1+v_4^1-v_3^1& \sim & 0\\ v_3^1+v_4^2-v_1^1-v_2^2-v_2^1 & \sim & 0\\ v_1^2+v_2^1+v_2^2-v_3^2-v_4^1 & \sim & 0\\ v_3^2-v_1^2-v_4^2 & \sim 0. \end{eqnarray*}$$

En sommant toutes les homologies ci-dessus, on obtient

$$v_1+v_2-v_3\sim v_1^1+v_1^2+v_2^1+v_2^2-v_3^1-v_3^2 \sim 0.$$

Les courbes fermées $v_1,v_2,v_3$ sont donc liées par une homologie, contrairement à ce qu’on aurait pu penser au départ.

On aurait également pu arriver au même résultat, en remplaçant les courbes $v_1,v_2,v_3$ par des subdivisions (ce que Poincaré s’autorise vraisemblablement à faire, voir nos commentaires du §5).

Traduction en termes modernes.

Ainsi, dans la définition des nombres de Betti $P_i$, il est crucial de tenir compte de toutes les combinaisons linéaires des homologies données par les frontières de toutes les variétés à $i+1$ dimensions. C’est pour formaliser cela que l’on est amené à utiliser le langage des modules. Si $V$ est (l’intérieur d’)une variété à bord, arêtes et coins de dimension $m$, et $i$ un entier compris entre $0$ et $m$, on a défini précédemment (voir les commentaires du §5) le $\mathbb{Z}$-module libre $C_i(V)$ et le morphisme de bord

$$d_i:C_i(V)\to C_{i-1}(V).$$

On a $d_{i-1}\circ d_{i}=0$ (les composantes de bord d’une variété sont des variétés fermées), ce qui implique que $\mathrm{Im}(d_{i})$ est un sous-module de $\mathrm{Ker}(d_{i-1})$.

Groupes d’homologie versus nombres de Betti

La définition moderne du nombre de Betti $P_i$ nécessite de prendre le quotient du module $\mathrm{Ker}(d_{i-1})$ par le sous-module $\mathrm{Im}(d_{i})$. Le concept abstrait de « quotient » ne deviendra vraiment familier des mathématiciens qu’au milieu du XXème siècle. C’est certainement pour cette raison que le groupe d’homologie $H_i(V,\mathbb{Z})$ n’apparaît jamais explicitement dans l’Analysis Situs. [3] Poincaré manipule toujours des éléments du complexe de chaînes $C_i(V)$ (et se demande ensuite s’ils sont, ou pas, homologues à $0$), mais il ne manipule jamais des classes d’homologie.

Nous verrons cependant que Poincaré réussit à élucider entièrement la structure du module $H_i(V,\mathbb{Z})$ (en particulier, sa partie de torsion) dans le deuxième complément à l’Analysis Situs, sans jamais introduire explicitement ce module. Autrement dit, Poincaré est bien conscient que la relation d’équivalence « être homologue » recèle plus d’informations sur la topologie d’une variété que les seuls nombres de Betti.

Décalage d’une unité.
Notons que, de nos jours, on appelle « $i$-ième nombre de Betti de $V$ » le rang du module $H_i(V,\mathbb{Z}):=\mathrm{Ker}(d_{i-1})/\mathrm{Im}(d_{i})$. C’est donc l’entier $P_i-1$ plutôt que l’entier $P_i$.

Les « nombres de Betti » de Poincaré ne sont pas les même que ceux de Betti.

La définition de Poincaré est une généralisation, pour les variétés de dimension arbitraire, de la notion d’« ordre de connexion d’une surface », introduite par Riemann dans sa thèse. Comme en témoigne l’expression « nombres de Betti », une telle généralisation avait déjà été esquissée par Enrico Betti une trentaine d’année avant Poincaré (voir notre article). Riemann lui-même avait réfléchi à la question (voir notre article).

Il est amusant de remarquer que les entiers $P_1,\dots,P_{m-1}$, que Poincaré nomme « nombres de Betti », diffèrent des entiers définis par Betti. En termes modernes :

• l’entier $P_i$ défini par Poincaré est le rang de la partie libre du $\mathbb{Z}$-module $H_i(V,\mathbb{Z})$, augmenté de $1$ ;
• l’entier $P_i$ défini par Betti est le nombre d’éléments d’une famille génératrice minimale du $\mathbb{Z}$-module $H_i(V,\mathbb{Z})$, augmenté de $1$. Autrement dit, les entiers définis par Poincaré « oublient » la partie de torsion du $\mathbb{Z}$-module $H_i(V,\mathbb{Z})$, alors que ceux définis par Betti en tiennent compte.

Poincaré ne signale à aucun moment cette différence, qui est pourtant assez subtile. Ne l’ayant pas remarquée, P. Heegaard croira avoir un contre-exemple à l’égalité des nombres de Betti $P_i$ et $P_{m-i}$, annoncée par Poincaré (voir, à ce sujet, les commentaires du §1 du premier complément).

Les nombres de Betti définis par Poincaré sont-ils finis ?

Poincaré tient apparemment pour acquis que les nombres $P_1,\dots,P_{m-1}$ sont finis. C’est clairement faux pour les variétés non-compactes en général. Surtout, ce n’est nullement évident pour les variétés compactes. En effet, le module $C_i(V)$ n’est jamais de type fini (ni même dénombrablement engendré). La finitude des nombres de Betti $P_1,\dots,P_{m-1}$, dans le cas où $V$ est compacte, est d’ailleurs très délicate à démontrer, et n’est vraie qu’à condition qu’on s’autorise à remplacer les sous-variétés par des subdivisions (voir ci-dessous).

Les nombres de Betti de Poincaré sont égaux aux nombres de Betti « modernes ».

Dans la partie cours moderne du site, nous adaptons une preuve de J. Cerf pour montrer que les nombres de Betti définis par Poincaré (auxquels on soustrait $1$) coïncident avec les nombres de Betti au sens de l’homologie singulière (et donc aussi avec les nombres de Betti au sens de l’homologie cellulaire ou simplifiable) [4] ; on y consacre un long article. Cette égalité est essentiellement équivalente à une conjecture formulée en 1940 par J. H. C. Whitehead, qui n’a été démontrée qu’en 1987 par F. Lalonde... Comme nous le verrons, la principale difficulté consiste à montrer que les nombres de Betti « à la Poincaré » de l’espace euclidien $\mathbb{R}^m$ sont nuls. Ce n’est nullement une trivialité !

De cette égalité, il découle en particulier que les nombres de Betti « à la Poincaré » d’une variété compacte sont finis.