Commentaires sur le §11 de l’Analysis Situs (Représentation par un groupe discontinu)

Dans le paragraphe 11 Poincaré propose une autre manière --- inspirée par sa théorie des groupes fuchsiens --- de construire des variétés, comme quotient de l’espace ordinaire par l’action propre et discontinue d’un groupe discret de transformations $S$ de l’espace. Il fait aussi le lien avec la construction du paragraphe précédent. En effet, si $D$ est un domaine fondamental pour l’action de ce groupe, on peut subdiviser son bord en faces (de codimension $1$) obtenues comme intersection $F$ de $D$ avec un translaté $S(D)$ adjacent à $D$. Si l’on note $F'$ la face commune à $D$ et $S^{-1} (D)$, alors l’espace quotient est également obtenu, comme dans le paragraphe précédent, à partir de $D$ en identifiant les faces $F$ et $F'$ (par paires).

Poincaré considère plus particulièrement l’exemple --- exemple 6 de Poincaré --- du quotient de $\mathbb{R}^3$ par le groupe $G_T$ engendré par les trois transformations

$$(x,y,z) \mapsto (x+1 , y , z), \ (x,y,z) \mapsto (x, y+1, z)$$

et

$$(x,y,z) \mapsto (ax+by , cx+dy , z+1),$$

où

$$T = \left( \begin{array}{cc} a & b \\ c & d \end{array} \right) \in \mathrm{SL} (2, \mathbb{Z} ).$$

Poincaré commence par montrer que le groupe $G_T$ opère librement et proprement discontinument sur l’espace $\mathbb{R}^3$. Autrement dit, seul l’élément neutre dans $G_T$ admet un point fixe dans $\mathbb{R}^3$, aucune orbite $\{ g (x) \; : \; g \in G_T\}$ ($x \in \mathbb{R}^3$) ne contient de point d’accumulation et tout point $x\in \mathbb{R}^3$ possède un voisinage qui est disjoint de tous ses translatés par les éléments de $G_T - \{ 1\}$.

Commentaires sur l’action du groupe $G_T$.

Puisque le groupe $G_T$ opère librement et proprement discontinument sur l’espace $\mathbb{R}^3$, le quotient $\mathbb{R}^3 / G_T$ est une variété de dimension $3$ dont le revêtement universel est $\mathbb{R}^3$.

Cet exemple (et certainement aussi la théorie des groupes fuchsiens) semble(nt) avoir inspiré à Poincaré la définition générale du groupe fondamental d’une variété que Poincaré donne dans le paragraphe suivant. [1] Dans le cas qui nous préoccupe ici, le groupe fondamental de la variété $\mathbb{R}^3 / G_T$ est naturellement isomorphe à $G_T$, puisque $\mathbb{R}^3$ est simplement connexe.

$$ $$

Le cube $P=[0,1]^3$ est un domaine fondamental pour l’action de $G_T$ sur $\mathbb{R}^3$, autrement dit toute orbite de $G_T$ intersecte $P$ et pas plus d’une fois l’intérieur de $P$. Poincaré subdivise alors la face inférieure $[0,1]^2 \times \{ 0 \}$ de $P$ en l’intersectant --- la face étant vue dans le plan $(x,y)$ --- avec les translatés par $\mathbb{Z}^2$ du parallélogramme $T^{-1} ([0,1]^2)$. Si $\sigma$ est une cellule de cette décomposition, on peut de même translater $T(\sigma)$ par un (unique) vecteur à coordonnées entières pour obtenir une cellule $\sigma'$ contenue dans la face supérieure $[0,1]^2 \times \{1 \}$ de $P$. Enfin Poincaré laisse intactes les quatre autres faces (verticales) du cube. Ainsi décomposé, le cube $P$ devient un polyèdre $P_T$ avec un nombre pair de faces.

Poincaré considère l’exemple où $T= \left( \begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix} \right)$. Dans ce cas, la face inférieure de $P=ABCDA'B'C'D'$ est décomposée en deux triangles $ABC$ et $BCD$, et la face supérieure est décomposée en les triangles correspondants $A'D'C'$ et $B'A'D'$. Les recollements sont illustrés sur la figure suivante.

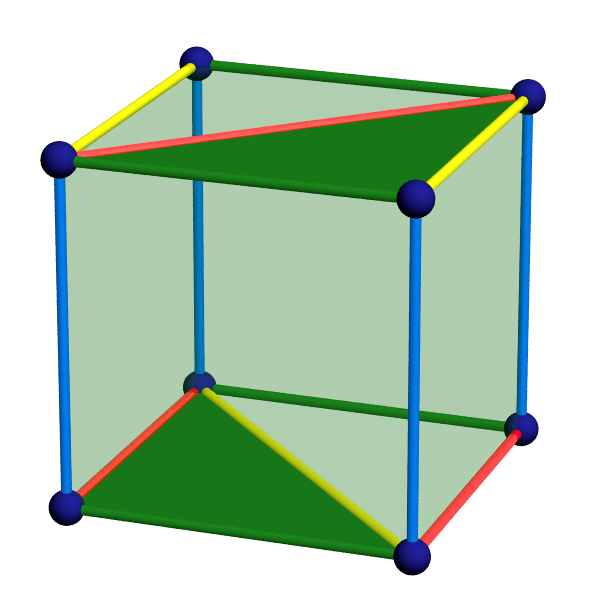
Poincaré remarque aussi que le nombre de cellules de $P_T$ augmente avec la taille des coefficients de la matrice $T$.

Commentaires sur la décomposition $P_T$.

Le cas où $T^{-1}= \left( \begin{smallmatrix} 1 & 1 \\ 1 & 2 \end{smallmatrix} \right)$ est instructif et illustré ci-dessous.

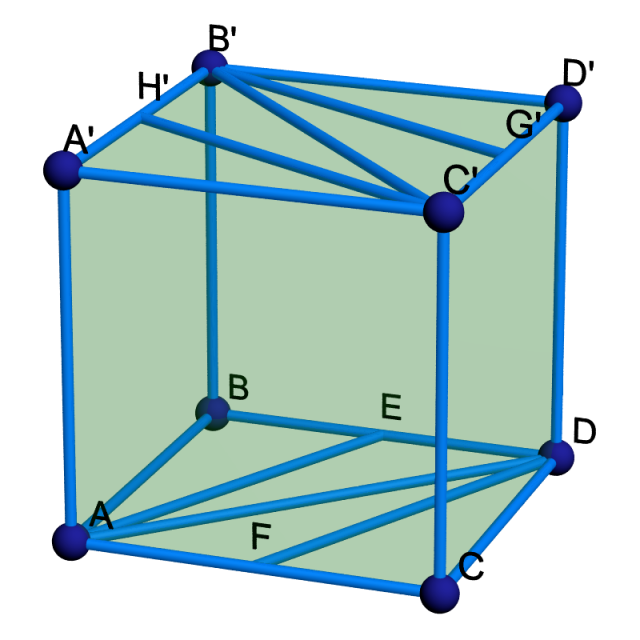
$$\begin{array}{|c|c|} \hline \sigma & \sigma ' \\ \hline ABE & C'B'G' \\ AED & A'H'C' \\ ADF & B'D'G' \\ FDC & H'B'C' \\ \hline \end{array}$$

Les faces inférieure et supérieure sont cette fois décomposées en 4 triangles chacune.

On note $P_T / \iota$ le quotient correspondant, où les faces $\sigma$ et $\sigma'$ sont identifiées ainsi que les faces verticales opposées. Noter que l’identification $\iota$ satisfait le critère d’orientabilité donné par Poincaré au paragraphe précédent.

Poincaré remarque que le quotient $P_T / \iota$ est homéomorphe à la variété de l’exemple 1, resp. exemple 2, lorsque $T=I$, resp. $T= \left( \begin{smallmatrix} 0 & 1 \\ -1 & 0 \end{smallmatrix} \right)$. Plus généralement, Poincaré vérifie que lorsqu’on quotiente par $\iota$, les points du bord de $P_T$ sont identifiés si et seulement s’ils appartiennent à une même orbite. Poincaré montre donc la proposition suivante.

Commentaires sur la proposition.

On appelle suspension d’un difféomorphisme $f : M \to M$ la variété obtenue en identifiant les points $(x,0)$ et $(f(x) , 1)$ dans le cylindre $M\times [0,1]$. Une matrice $T \in \mathrm{M}_2 (\mathbb{Z} )$ induit --- par action linéaire sur $\mathbb{R}^2$ --- une application $f_T : \mathbb{R}^2 / \mathbb{Z}^2 \to \mathbb{R}^2 / \mathbb{Z}^2$ qui est un difféomorphisme si et seulement si $T \in \mathrm{GL} (2, \mathbb{Z})$. Alors la suspension $M_T$ du tore $\mathbb{R}^2 / \mathbb{Z}^2$ par le difféomorphisme $f_T$ est une variété de dimension $3$ qui est orientable si et seulement si $T \in \mathrm{SL} (2 , \mathbb{Z})$. La variété $M_T$ est homéomorphe à la variété $\mathbb{R}^3 / G_T$.

Dans une Note de 1892, Poincaré affirme que deux variétés $M_T$ et $M_{T'}$ sont homéomorphes si et seulement si $T$ (ou $T^{-1}$) et $T'$ sont conjuguées dans $\mathrm{GL} (2, \mathbb{Z} )$ ; voir ici pour une démonstration. Le groupe fondamental de $M_T$ est isomorphe à $G_T$.

Dans le paragraphe suivant Poincaré montre que les exemples 3 et 5 ne sont pas homéomorphes à des variétés de la forme $\mathbb{R}^3 / G_T$ : leurs groupes fondamentaux sont finis, et leurs revêtements universels sont homéomorphes à la sphère $\mathbb{S}^{3}$ et non pas à l’espace $\mathbb{R}^3$. Noter que les exemples 3 et 5, ainsi que la variété dodécaédrique de Poincaré, peuvent être obtenus comme quotients de $\mathrm{SO} (3)$ --- ou mieux de $\mathrm{SU}(2)$, qui est simplement connexe --- par certains sous-groupes finis.

Dans le troisième complément, Poincaré revient sur cette famille d’exemples (et considère plus généralement des suspensions de surfaces réelles de genre arbitraire) en partant d’une construction différente, plus algébrique.

La matrice $T$ est soit périodique (ou elliptique), soit parabolique, c’est-à-dire conjuguée à la matrice $\left( \begin{smallmatrix} 1 & n \\ 0 & 1 \end{smallmatrix} \right)$ pour un certain $n \in \mathbb{Z}$, soit hyperbolique, c’est-à-dire diagonalisable à valeurs propres distinctes.

Si $T$ est périodique d’ordre $n$, alors la variété $M_{T^n} = M_{\rm I}$ est homéomorphe au tore de dimension $3$ et est un revêtement (cyclique) de degré $n$ de la variété $M_T$. On peut d’ailleurs montrer que $M_T$ est une variété euclidienne, c’est-à-dire un quotient de l’espace euclidien $\mathbb{E}^3$ par un sous-groupe discret et sans torsion du groupe des isométries de $\mathbb{E}^3$. Un tel groupe est appelé groupe cristallographique. Ces groupes ont été classifiés par Bieberbach [2]. Toute variété euclidienne est homéomorphe à une variété $M_T$ pour une certaine matrice périodique $T$ [3].

Si $T$ est parabolique ou hyperbolique, alors on ne peut plus réaliser le groupe $G_T$ comme un sous-groupe d’isométries euclidiennes. On peut toutefois munir l’espace $\mathbb{R}^3$ d’une métrique pour laquelle le groupe $G_T$ s’identifie à un sous-groupe discret d’isométries. Tout ceci est détaillé ici.

En bref, lorsque $T$ est parabolique, la variété $M_T$ est un quotient compact du groupe de Lie $\mathrm{NIL}$, aussi appelé groupe d’Heisenberg, sous-groupe de $\mathrm{GL}_3 (\mathbb{R} )$ des matrices de la forme

$$\left( \begin{array}{ccc} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \end{array} \right) , \quad x , y , z \in \mathbb{R}.$$

Le groupe $\mathrm{NIL}$ est une extension centrale de $(\mathbb{R}^2, +)$ par $(\mathbb{R},+)$ :

$$1 \to \mathbb{R} \to \mathrm{NIL} \to \mathbb{R}^2 \to 1.$$

Et, de même, lorsque $T$ est hyperbolique, la variété $M_T$ est un quotient compact du groupe de Lie $\mathrm{SOL}$, extension scindée de $\mathbb{R}$ par $\mathbb{R}^2$.

Les géométries euclidiennes, NIL et SOL figurent parmi les huits géométries --- dites « de Thurston » --- et qui permettent de géométriser toutes les variétés de dimension $3$ (après découpage canonique) [4]. Les autres géométries sont la géométrie sphérique, qui permet par exemple de géométriser la variété hypercubique ou la variété dodécaédrique de Poincaré, la géométrie hyperbolique, qui permet par exemple de géométriser la variété dodécaédrique de Seifert-Weber, les géométries produit $\mathbb{S}^2 \times \mathbb{R}$ et $\mathbb{H}^2 \times \mathbb{R}$ qui permettent par exemple de géométriser les variétés de dimension 3 obtenues en formant le produit d’une surface par un cercle, et enfin la géométrie $\mathrm{SL}(2 , \mathbb{R})$ qui permet par exemple de géométriser les variétés de dimension $3$ obtenues comme fibré unitaire tangent d’une surface hyperbolique.