Commentaires sur le §5 de l’Analysis Situs (Homologies)

Les paragraphes 5 et 6 sont à la source de tout un pan des mathématiques du XXème siècle : Poincaré y définit le concept d’homologie.

Pour mesurer la complexité de la topologie d’une surface compacte, fermée ou non, Riemann avait introduit la notion d’ordre de connexion. Le but de Poincaré est de généraliser cette notion en dimension supérieure. Riemann lui-même, puis Betti, s’étaient déjà engagés dans ce chemin, mais ils n’avaient pas réussi à mettre sur pied des définitions précises (voir nos articles à ce sujet, ici, et là).

L’ordre de connexion selon Riemann d’une surface fermée $S$ peut être défini de différentes manières (voir quelques exemples dans nos commentaires du §6).

On peut tout d’abord compter le nombre minimal de courbes fermées simples que l’on doit tracer sur $S$, pour découper $S$ en un disque, puis rajouter $1$. Cette définition se généralise très mal au cas où $S$ est une variété de dimension $m>2$, [1] d’autant plus qu’on aimerait alors remplacer les courbes tracées sur $S$ par des sous-variétés de $S$ de dimension $p$ arbitraire, afin de mesurer la « complexité de $S$ en dimension $p$ » pour chaque $p$.

Mais on peut aussi définir l’ordre de connexion comme l’entier minimal $k$ tel que, si on trace n’importe comment $k$ courbes fermées simples orientées sur $S$, alors certains morceaux de ces courbes formeront la frontière orientée d’un morceau de $S$. Cette définition semble beaucoup plus apte à la généralisation en dimension supérieure, comme l’avait déjà remarqué Riemann (voir, à nouveau, notre article). C’est effectivement la voie qu’emprunte Poincaré.

Contrairement à Riemann et Betti, Poincaré ne va pas se contenter de définir des ordres de connexions pour les variétés de dimension quelconque. Il va introduire presque tous les ingrédients du concept d’homologie : il définit une notion de bord, il comprend qu’il faut considérer des combinaisons formelles de sous-variétés, il introduit la relation d’équivalence « être homologue », etc.

Homologies, selon Poincaré

Plus concrêtement, l’objet du §5 est de définir une relation d’équivalence (l’« homologie ») sur les combinaisons linéaires de sous-variétés d’une variété $V$. Examinons le texte de Poincaré :

Considérons une variété $V$ à $p$ dimensions ; soit maintenant $W$ une variété à $q$ dimensions ($q\leq p$) faisant partie de $V$ [en termes modernes : une sous-variété de dimension $q$ de $V$]. Supposons que la frontière complète de $W$ se compose de $\lambda$ variétés continues [c’est-à-dire, en termes modernes, connexes] à $q−1$ dimensions [notées $v_1,\dots,v_\lambda$].

Nous exprimerons ce fait par la notation

$$v_1+\dots+v_\lambda\sim 0.$$

Plus généralement la notation

$$k_1v_1+k_2v_2\sim k_3v_3+k_4v_4,$$

où les $k_i$ sont des entiers et les $v_i$ des [sous-]variétés à $q−1$ dimensions [de $V$], signifiera qu’il existe une variété $W$ à $q$ dimensions faisant partie de $V$ [c’est-à-dire une sous-variété de dimension $q$ de $V$] et dont la frontière complète se composera de $k_1$ variétés peu différentes de $v_1$, de $k_2$ variétés peu différentes de $v_2$, de $k_3$ variétés peu différentes de la variété opposée à $v_3$ et de $k_4$ variétés peu différentes de la variété opposée à $v_4$.

Les relations de cette forme pourront s’appeler homologies.

Les homologies peuvent se combiner comme des équations ordinaires.

Cette « définition » appelle de nombreux commentaires, et soulève tout autant de questions.

Orientation.
Dans la définition ci-dessus, la variété $W$ est tacitement supposée orientée, et les composantes de la frontière complète de $W$ sont tacitement supposées munies de leur orientation « en tant que bord ». La variété $V$ n’est pas nécessairement orientée, ni même orientable.

Problème de définition de la « frontière complète ».
Le premier point de la définition ne pose guère de problème. Bien sûr, d’un point de vue strictement formel, tout cela n’a aucun sens puisque la frontière complète d’une variété $W$ n’est pas bien définie (elle dépend des équations utilisées pour définir $W$, voir les commentaires du §1). Mais, pour rétablir la situation, il suffit de modifier la définition de variété donnée par Poincaré au §1 afin d’avoir une bonne notion de frontière. On peut utiliser ici la notion de variété à bord (mais ça ne sera pas suffisant dans la suite), ou mieux la notion de variété polyédrale que nous avons définie dans les commentaires du §1 (ceci permet de rester au plus proche des définitions de Poincaré, et surtout d’obtenir une théorie de l’homologie isomorphe à l’homologie singulière, voir le cours moderne).

Linéarité.
Dès le premier point de la définition ci-dessus, on voit apparaître des sommes de sous-variétés. Poincaré pourrait écrire

$$v_1\cup\dots\cup v_\lambda\sim 0,$$

mais il choisit sciemment de remplacer l’union par une somme formelle, et écrit

$$v_1+\dots+v_\lambda\sim 0.$$

C’est sans importance à ce stade puisque les $v_i$ sont deux à deux disjointes (ce sont les composantes connexes d’une « frontière complète ») ; l’union des $v_i$ détermine donc $v_i$. Dès le second point, Poincaré manipule des multiples entiers d’une variété ; ici il devient nécessaire d’utiliser des sommes formelles plutôt que des unions, afin de distinguer $v_i+v_i$ de $v_i$. La phrase « Les homologies peuvent se combiner comme des équations ordinaires » peut sembler obscure. À la lecture du texte de Poincaré, on ne sait pas s’il s’agit d’un énoncé qui découle des définitions précédentes, ou bien de la fin de la définition de la relation $\sim$.

À notre avis, cette phrase fait partie de la définition, et il faut la comprendre comme suit : Poincaré veut pouvoir enchaîner et ajouter les homologies ; il force donc la relation $\sim$ à être transitive et compatible avec les combinaisons linéaires à coefficients entiers. En termes modernes, Poincaré considère l’ensemble des combinaisons linéaires formelles à coefficients entiers des variétés continues à $q-1$ dimensions dans $V$, c’est-à-dire le $\mathbb{Z}$-module libre engendré par les variétés continues à $q-1$ dimensions dans $V$. Les deux premiers points de la définition de Poincaré fournissent des « homologies », qui engendrent une relation d’équivalence entre les éléments de ce $\mathbb{Z}$-module. Le troisième point de la définition signifie qu’on sature cette relation d’équivalence par combinaisons linéaires (à coefficients entiers).

Cette idée de manipuler des combinaisons linéaires formelles de sous-variétés nous semble un des apports importants de Poincaré : c’est un des ingrédients qui lui permet d’aller beaucoup plus loin que Riemann et Betti dans leurs tentatives de définir des « ordres de connexion » pour les variétés de dimension arbitraire.

Variétés « peu différentes ».
Dans sa définition des « homologies », Poincaré utilise la notion de « variété peu différente de $v$ ». Que signifie cette expression ?

Il nous semble qu’elle correspond à la possibilité de déplacer $v$ par une petite isotopie.

Rappelons que deux sous-variétés (éventuellement à bords, ou polyédrales) $v,v'$ d’une même variété ambiante $V$ sont dites isotopes s’il existe un chemin continu de sous-variétés de $V$ joignant $v$ à $v'$. Définir formellement la notion de « chemin continu de sous-variétés » est facile : on demande l’existence d’un chemin continu de familles d’équations locales, ou d’un chemin continu de familles de paramétrages locaux, ou d’un chemin continu de systèmes de cartes.

Quand Poincaré utilise l’expression « variétés peu différentes », il nous semble qu’il veut typiquement prendre en compte la situation suivante. Considérons la surface $W$ consitutée d’un ruban de Möbius $R$ privé d’une bande $B$, comme sur la figure ci-dessous.

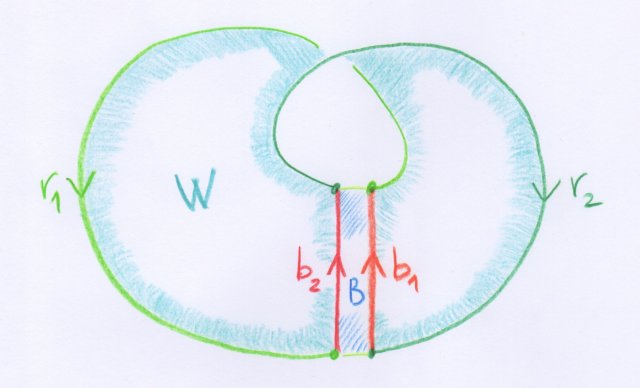
Cette surface $W$ est en fait (à difféomorphisme près) un simple rectangle. C’est donc une variété (orientable) à $2$ dimensions au sens de la première définition de Poincaré, dont la frontière complète est constituée de quatre arcs orientés : les deux composantes $b_1,b_2$ du bord de la bande $B$ (qui héritent d’orientations parallèles), et deux arcs $r_1,r_2$ contenus dans le bord du ruban de Möbius $R$ (voir dessin). On a donc

$$r_1+r_2+b_1+b_2\sim 0.$$

Si la bande $B$ devient de plus en plus fine, les deux arcs orientés $b_1,b_2$ tendent vers un même arc $b$. On a donc très envie d’écrire

$$2b+r_1+r_2\sim 0.$$

Mais $R\setminus b$ n’est pas une variété au sens défini par Poincaré, et il ne peut exister aucune variété contenant deux copies de $b$ dans son bord. Pour avoir une homologie $2b+r_1+r_2\sim 0$, il faut s’autoriser à changer $2b$ en $b_1+b_2$, c’est-à-dire à déplacer chaque copie de $b$ par une petite isotopie. Il nous semble que l’expression « deux variétés peu différentes de $b$ » recèle la possibilité remplacer $2b$ par $b_1+b_2$.

On notera par ailleurs que Poincaré s’autorise, en plusieurs points de son mémoire, à perturber — sans le dire — les sous-variétés qui apparaissent dans les homologies par de petites isotopies. Ainsi, au §9, il suppose toujours que les sous-variétés considérées sont en position générique (ce qui n’est vrai — et Poincaré le sait parfaitement — que si on se donne le droit de perturber les variétés par de petites isotopies).

Il est difficile de savoir si Poincaré considère comme un fait évident que « deux variétés isotopes sont homologues » [2], ou si l’assertion « deux variétés isotopes sont homologues » fait partie de sa définition de la relation « être homologue ». Nous penchons plutôt pour la première possibilité. En effet, l’assertion « isotope implique homologue » est assez similaire à l’assertion « toute sous-variété fermée de $\mathbb{R}^n$ est homologue à $0$ » que Poincaré semble considérer comme évidente (voir par exemple §6 et §9).

Subdivision des sous-variétés
Si on s’en tient stricto sensu aux définitions de Poincaré, l’assertion « isotope implique homologue » est fausse. Cependant, elle devient vraie si on s’autorise à « subdiviser les sous-variétés ».

Si $v,v_1,\dots,v_n$ sont des sous-variétés à bord (ou polyédrales), on dira que $v_1,\dots,v_n$ est une subdivision de $v$, si les intérieurs des sous-variétés $v_1,\dots,v_n$ sont deux à deux disjoints, et si l’union de ces sous-variétés est égale à $V$.

Si on identifie $v$ à $v_1+\dots+v_n$ dès lors que $v_1,\dots,v_n$ est une subdivision de $v$, alors deux sous-variétés polyédrales fermées isotopes sont homologues. Ce fait est cependant bien loin d’être trivial ! On pourra lire à ce sujet la partie de notre « cours moderne » consacrée à l’« homologie à la Poincaré ».

Dans sa définition des homologies, il est probable que Poincaré s’autorise à remplacer toute sous-variété $v$ par une combinaison du type $v_1+\dots+v_n$ où $v_1,\dots,v_n$ est une subdivision de $v$, et vice-versa. Par exemple, si $v^+$ et $v^-$ désignent les hémisphères nord et sud de la sphère unité, nous sommes persuadés que Poincaré aurait considéré que $v^++v^-$ est homologue à $0$ car $v^+$ et $v^-$ forment le bord (il aurait dit la « frontière complète ») de la boule unité (même si, formellement, c’est faux : le bord de la boule unité est une sphère ; pas la somme de deux hémisphère). C’est d’autant plus vraisemblable quand on se souvient que la définition que Poincaré donne de la frontière complète est « bancale » : avec sa définition, on peut remplacer la frontière complète d’une sous-variété par une subdivision de celle-ci, en changeant les équations qui définissent cette sous-variété (voir nos commentaires du §1).

Une traduction en termes modernes.

Comment transcrire, en termes modernes, la définition de l’homologie de Poincaré ? Voici une proposition de traduction (nous utilisons les sous-variétés polyédrales définies dans les commentaires du §1) :

On considère, pour tout $q\in \{0,\dots,p\}$, le $\mathbb{Z}$-module libre $C_{q}(V)$ engendré par les sous-variétés polyédrales connexes orientées de dimension $q$ de $V$. [3] On définit alors, pour tout $q$, un opérateur bord

L’image par $\partial_q$ d’une sous-variété polyédrale $W$ est la somme formelle des $(q-1)$-faces de $W$, munies de leurs orientations comme bord. Ceci définit $\partial_q$ sur une base de $C_q(V)$, et on étend $\partial_q$ à $C_q(V)$ par linéarité. On dit alors que deux éléments de $C_q(V)$ sont « homologues » si et seulement si leur différence est dans le noyau de $V$. Par construction, la relation d’homologie est compatible avec les combinaisons linéaires.

Si on veut tenir compte du fait que Poincaré s’autorise probablement tacitement à remplacer une sous-variété $v$ par la somme $v_1+\dots+v_n$ des éléments d’une subdivision $v_1,\dots,v_n$ de $v$, alors on doit quotienter, pour tout $k$, le module $C_k(V)$ par la relation d’équivalence $v\sim v_1+\dots+v_n$, et remarquer que l’opérateur de bord $\partial_q$ passe au quotient (voir notre cours moderne sur l’homologie à la Poincaré).

Homologie relative du couple $(V,\partial V)$

Poincaré conclut le §5 en introduisant une notation qui ne pose pas, à notre avis, de problème particulier :

supposons que l’on ait

$$k_1v_1+k_2v_2+\dots+k_pv_p\sim w_1+w_2+\dots+w_q$$

et que les variétés $w_1,w_2,\dots,w_q$ fassent partie de la frontière de $V$ ; nous écrirons quelquefois

$$k_1v_1+k_2v_2+ \dots +k_pv_p\sim \epsilon.$$

Le choix de la lettre $\epsilon$ montre clairement une intention de considérer que toute variété contenue dans le bord de $V$ est « négligeable du point de vue de l’homologie ». Cette notation est donc un pas vers ce qu’on appellerait aujourd’hui l’« homologie relative du couple $(V,\partial V)$ » (voir le cours moderne).