Commentaires sur le §9 de l’Analysis Situs (Intersection de deux variétés)

1. Commençons par reformuler la définition du nombre d’intersection donnée par Poincaré. Notons $n$ la dimension de la variété ambiante que l’on suppose orientée.

Commentaires sur la formulation de Poincaré

Dans son article Poincaré donne une définition équivalente mais plus formelle en terme de déterminants.

Ainsi, si la variété ambiante est supposée être l’espace euclidien $\mathbb{R}^n$ et si $v$ et $v'$ sont deux sous-variétés au sens de la deuxième définition de Poincaré, c’est-à-dire localement images d’immersions $(y_1 , \ldots , y_p) \mapsto (x_1 , \ldots , x_n)$, alors Poincaré définit pour tout couple $(x,x') \in v \times v'$ le nombre $S(x,x') \in \{ -1 , 0 , +1\}$ comme le signe du déterminant (de taille $n \times n$)

$$\tag{1} \left| \begin{array}{c} \partial x_i / \partial y_j \\ \partial x_i ' / \partial y_k' \end{array} \right| , \quad 1 \leq i \leq n , \ 1 \leq j \leq p, \ 1 \leq k \leq n-p, $$

dont il démontre qu’il est bien défini, i.e. qu’il ne dépend que de $x$ et $x'$ et pas du choix des paramétrages (du moment que ceux-ci définissent la bonne orientation de $v$ et $v'$), et pose ensuite

$$N(v , v') = \sum_{x=x'} S(x,x').$$

Supposons maintenant que l’espace ambiant soit une variété, au sens de la première définition de Poincaré, donnée par une équation $G=0$ où $G$ est une submersion $\mathbb{R}^t \to \mathbb{R}^{t-n}$. Supposons de plus que $v$ et $v'$ sont elles-mêmes données par les équations respectives

$$G=0=F \quad \mbox{ et } \quad G=0=F'.$$

Poincaré pose alors

$$N(v , v') = \sum_{x=x'} S(x,x')$$

où, cette fois, pour tout couple $(x,x') \in v \times v'$, $S(x,x')$ désigne le signe du déterminant (de taille $t \times t$)

$$\tag{2} \left| \partial G_\gamma / \partial x_i \ \partial F_\beta ' / \partial x_i \ \partial F_{\alpha} / \partial x_i \right|_{1 \leq i \leq t , \ 1 \leq \gamma \leq t-n, \ 1 \leq \beta \leq p, \ 1 \leq \alpha \leq n-p}. $$

Poincaré montre que ces définitions sont bien compatibles mais ne demande jamais explicitement que les sous-variétés ne s’intersectent qu’un nombre fini de fois ni que les intersections soient transverses. Cette dernière condition équivaut au fait que le déterminant (1) (ou (2) selon la définition de variété que l’on voudra prendre) est non nul. Poincaré semble donc considérer que le nombre d’intersection local est nul lorsque les sous-variétés ne s’intersectent pas transversalement. Cela ne correspond pas à la bonne notion de nombre d’intersection local comme le montre par exemple le cas de l’intersection, dans le plan $(x,y)$, de l’axe des abscisses avec la courbe d’équation $y=x^3$ en le point $(0,0)$.

$$ $$

Noter que le nombre d’intersection $N(v,v')$ change de signe si l’on change l’orientation de l’une des variétés $v$ ou $v'$ ou encore de la variété ambiante, et l’on a :

$$\tag{3} N(v', v) = (-1)^{\mathrm{dim} v \cdot \mathrm{dim} v'} N(v,v'). $$

Dans la suite 2 et 3 ci-dessous on supposera que l’espace ambiant est une variété orientée $M$ de dimension $n$ que l’on fixe une fois pour toutes. On supposera en outre que $M$ est compacte ou bien l’intérieur d’une variété compacte à bord $\overline{M}$ auquel cas on notera abusivement $\partial M$ le bord de $\overline{M}$.

$$ $$

2. Poincaré énonce ensuite le résultat suivant.

Démonstration moderne de ce théorème

Une démonstration moderne de ce théorème résulte d’un Théorème de Thom, selon lequel toute classe d’homologie rationnelle peut être représentée par une sous-variété, et de l’interprétation géométrique du produit d’intersection.

$$ $$

Pour citer Dieudonné [2] :

The proof given by Poincaré (probably inspired by Kronecker [3]) for $p=1$ seems correct, at least when the $V_j$ are distinct. (The general case is not considered.) But his attempt to prove the result for $p>1$ is totally unconvincing. [4]

Commençons donc par donner la démonstration de Poincaré dans le cas $p=1$.

Démonstration du théorème dans le cas $p=1$. Pour démontrer l’implication directe, au vu de la définition de l’homologie donnée par Poincaré, il suffit de vérifier que si $W$ est un ouvert connexe de bord $\partial W = V_1 + \ldots +V_t$, et si $C$ est une courbe orientée fermée, ou de bord trivial relativement au bord de $M$, et qui intersecte transversalement les $V_j$, alors

$$N(C , V_1 ) + \ldots + N(C , V_t ) = 0.$$

Pour montrer cette dernière assertion Poincaré raisonne comme suit. Si la courbe $C$ est fermée, elle doit traverser la frontière de $W$ autant de fois en un sens (par exemple du complémentaire de $\overline{W}$ vers $W$) que dans l’autre sens (ici de $W$ vers le complémentaire de $\overline{W}$). Ceci reste d’ailleurs vrai si $C$ est une courbe dont les deux extrémités appartiennent au bord $\partial M$, puisqu’une telle courbe commence et termine en dehors de $\overline{W}$. Dans tous les cas le nombre d’intersection $N(C , \partial W)$ est la somme d’un nombre égal de $+1$ et de $-1$ ; il est donc nul.

Réciproquement, supposons que la somme $\sum_i k_i V_i$ ($k_i \in \mathbb{Q}^\times$) soit non nulle dans $H_{n-p} (M , \mathbb{Q})$. Il découle de l’implication directe — que nous venons de démontrer — que si l’une des $V_i$ est homologue à une combinaison rationnelle des autres, on peut toujours la remplacer par cette combinaison linéaire sans changer la valeur de son nombre intersection avec n’importe quelle courbe orientée fermée, ou de bord trivial relativement au bord de $M$. On peut donc dorénavant supposer qu’il n’existe aucune homologie rationnelle non triviale entre les $V_i$.

Commentaires sur cette première réduction

On prendra garde au fait que la réduction ci-dessus ne marche pas en homologie entière. D’ailleurs si le théorème reste vrai en homologie entière pour $p=1$ (car $H_{n-1} (M , \mathbb{Z})$ est toujours sans torsion d’après le théorème des coefficients universels), il est faux en général. Il existe en effet une variété $M$ telle que $H_{n-2} (M , \mathbb{Z})$ contienne une classe de torsion ; on peut d’ailleurs prendre $n=3$ et $M$ compacte. Il correspond à une telle classe une sous-variété $V \subset M$ qui ne borde pas mais telle que $k V$ (avec $k \in \mathbb{Z}$, $k \neq 0$) soit triviale en homologie. Si $C\subset M$ est une surface fermée qui intersecte $V$ transversalement, on a alors

$$N(C , V) = \frac{1}{k} N( C , k V) = 0.$$

$$ $$

Ceci implique, si $M$ est sans bord, que le complémentaire $W$ de la réunion $V_1 \cup \ldots \cup V_t$ est connexe, puisque dans le cas contraire le bord de n’importe laquelle des composantes connexes de ce complémentaire fournirait une homologie non-triviale entre des $V_i$. Et si $M$ a un bord non vide, cela implique de la même manière que chaque composante du complémentaire doit être incident au bord.

Commentaires sur ce dernier paragraphe

Dans le paragraphe précédent l’argument de Poincaré suppose implicitement que si le bord d’une composante connexe du complémentaire de la réunion $V_1 \cup \ldots \cup V_t$ contient une partie de l’un des $V_i$ alors il contient $V_i$ toute entière. C’est évidemment faux en général comme le montre la figure ci-dessous. On peut toutefois se ramener à cette situation en remplaçant les $V_i$ par des sous-variétés qui leur sont homologues.

$$ $$

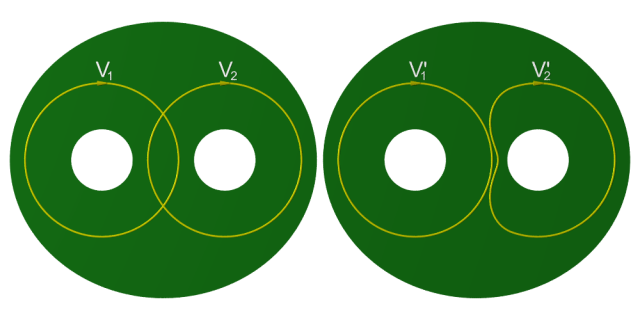
Considérons donc un petit segment rencontrant $V_1$ transversalement en un unique point $x$ et disjoint des autres $V_i$. Les deux extrémités de ce segment appartiennent à $W$ et peuvent donc soit être connectées par un lacet disjoint de la réunion $V_1 \cup \ldots \cup V_t$ soit être toutes les deux reliées au bord $\partial M$ par deux arcs disjoints de $V_1 \cup \ldots \cup V_t$. On obtient ainsi une courbe $C$ fermée, ou de bord trivial relativement au bord de $M$, qui intersecte transversalement les $V_j$ et vérifie

$$\sum_{i=1}^t k_i N(C , V_i ) = k_1 \neq 0.$$

C.Q.F.D.

Commentaires supplémentaires sur la preuve de Poincaré

Au cours de cette preuve Poincaré semble suggérer que chaque $V_i$ intervient au plus deux fois dans le bord de chaque composante connexe du complémentaire de la réunion $V_1 \cup \ldots \cup V_t$. On notera que cette affirmation implique que les homologies entre sous-variétés de codimension $1$ s’obtiennent toutes comme combinaison linéaire d’homologies dont tous les coefficients sont égaux à $\pm 1$. En particulier cela implique que $H_{n-1} (M , \mathbb{Z})$ est libre ; ce qui est bien vrai d’après le théorème des coefficients universels.

$$ $$

3. Résumons maintenant la « démonstration » du théorème que donne Poincaré lorsque $p\geq 2$.

Supposons que $M$ est une variété, au sens de la première définition de Poincaré, donnée par des équations $F_{\alpha} =0$ (et des inégalités) et que la sous-variété $C\subset M$, de dimension $p$, est donnée par $n-p$ équations supplémentaires $F_\gamma ' =0$.

En ce qui concerne les sous-variétés $V_i\subset M$, de codimension $p$, Poincaré suppose que l’ensemble des points de leur réunion $V_1 \cup \ldots \cup V_t$ vérifient $p-1$ équations supplémentaires $\Phi_\nu =0$. Autrement dit, Poincaré suppose que la réunion $V_1 \cup \ldots \cup V_t$ est contenue dans une sous-variété $W \subset M$, de dimension $n-p+1$, déterminée par les équations $F_\alpha =0$ et $\Phi_\nu =0$, et que chaque sous-variété $V_i$, de codimension $1$ dans $W$, est déterminée par une équation supplémentaire $F_i '' =0$.

Commentaires sur l’existence de $W$

En supposant la somme $\sum_i k_i V_i$ nulle en homologie rationnelle dans $M$, on peut en effet toujours « élargir » une sous-variété de $M$ ayant pour bord orienté $\sum_i k_i V_i$ et ainsi obtenir une sous-variété immergée (à bord) $W \subset M$ de dimension $n-p+1$ et dont l’intérieur contient tous les $V_i$. En l’absence de cette supposition il n’est pas clair du tout qu’une telle sous-variété $W$ existe toujours.

Reste toutefois que les variétés au sens de la première définition de Poincaré ont toutes leurs classes caractéristiques nulles. [5] En particulier chaque $V_i$ borde (abstraitement). On peut donc trouver une variété (à bord) $\overline{W}$ de dimension $n-p+1$ dont l’intérieur contient des copies disjointes $\overline{V}_i$ des $V_i$. Reste alors à trouver comment étendre les applications naturelles $\overline{V}_i \to V_i$ en une application $\overline{W} \to M$ $\ldots$

$$ $$

Poincaré remarque ensuite que

$$N(C, V_i) = N(C \cap W , V_i)$$

et que $C \cap W$ est une courbe dans $W$.

Commentaires sur cette identité

Il faut bien sûr que les sous-variétés $C$ et $W$ s’intersectent transversalement pour que ceci ait un sens. À ceci près, l’énoncé est correct. Maintenant, en supposant la somme $\sum_i k_i V_i$ nulle en homologie rationnelle dans $M$, on a vu que l’on peut effectivement construire la variété $W$. Comme l’affirme Poincaré un peu plus bas, on peut en outre s’arranger pour que la somme $\sum_i k_i V_i$ soit nulle en homologie rationnelle dans $W$ (c’est d’ailleurs immédiat pour la construction que l’on a proposé ci-dessus). Le sens directe du théorème appliqué à $W$ (et donc dans le cas démontré où les sous-variétés $V_i$ sont de codimension $1$) implique que

$$\sum_{i=1}^t k_i N(C,V_i) = \sum_{i=1}^t k_i N(C\cap W , V_i) =0.$$

Poincaré donne donc les grandes lignes d’une démonstration complète de l’implication directe dans le théorème.

$$ $$

Poincaré remarque ensuite que si la somme $\sum_i k_i V_i$ est nulle en homologie rationnelle dans $W$, alors elle est encore nulle en homologie rationnelle dans $M$. La réciproque est bien sûr fausse en général mais Poincaré affirme que si la somme $\sum_i k_i V_i$ est nulle en homologie rationnelle dans $M$, on peut toujours, en choisissant convenablement les fonctions $\Phi_\nu$, trouver une sous-variété $W$ comme ci-dessus et pour laquelle la réciproque est vérifiée.

On est alors réduit au cas $p=1$ démontré ci-dessus. Et le théorème est démontré en toute généralité.

Commentaires sur cette dernière étape

Cette dernière étape pose en fait de sérieux problèmes.

En premier lieu on a en déjà fait remarquer que l’existence de la sous-variété $W$ n’est pas claire si l’on ne suppose pas que la somme $\sum_i k_i V_i$ est nulle en homologie rationnelle dans $M$. Mais il y a pire, l’implication réciproque dans le théorème ne se réduit pas si facilement au cas $p=1$.

Supposons en effet que la somme $\sum_i k_i V_i$ est non nulle en homologie rationnelle dans $M$ et supposons qu’il existe bien une sous-variété $W$ comme l’affirme Poincaré. Il est alors bien certain ---- comme le remarque Poincaré ---- que $\sum_i k_i V_i$ est non nulle en homologie rationnelle dans $W$. Et on peut donc appliquer à $W$ le théorème (en codimension $1$). On obtient ainsi une courbe $c$ sur $W$ fermée, ou de bord nul relativement au bord de $W$, telle que la somme $\sum_i k_i N(c, V_i)$ soit non nulle. Reste que la démonstration est loin d’être terminée : il n’est en effet pas clair du tout qu’il existe une sous-variété fermée $C \subset M$ de dimension $p$ telle que $C$ intersecte transversalement $W$ et $C\cap W = c$ !

Les deux trous ci-dessus ont été mis en évidence par Heegaard [6] qui considérait d’ailleurs que la dualité de Poincaré était fausse en général et donna même une « contre-exemple » :-)

On renvoie le lecteur intéressé par la réponse de Poincaré à la Note de 1892 (et nos commentaires) ainsi qu’au premier complément (et nos commentaires). En bref, Poincaré y concède que le second trou est sérieux mais montre que le « contre-exemple » d’Heegaard n’en est pas un et, surtout, donne une preuve nouvelle (et correcte cette fois :-)) d’une version sensiblement plus forte de la dualité de Poincaré.

$$ $$

4. Poincaré tire de son théorème le (célèbre et fondamental) corollaire suivant.

Ce théorème n’a, je crois, jamais été énoncé ; il était cependant connu de plusieurs personnes qui en ont même fait des applications.

Commentaires sur la citation

Poincaré ne donne pas de noms mais pense certainement au moins à Picard. En fait, celui-ci avait déjà énoncé ce théorème en 1889 sous la forme suivante [7] :

Pour un domaine fermé $\delta$, les différents nombres $p_m$, pour les diverses valeurs de $m$, s’associent deux à deux, et on démontre que $p_m = p_{n-m}$.

Picard utilise sans preuve ce théorème pour le cas $n=4$, dans son étude des surfaces complexes non singulières.

$$ $$

Démonstration. On oriente $M$ et on choisit deux ensembles maximaux de sous-variétés compactes $\{C_1 , \ldots , C_{\lambda} \}$ et $\{V_1 , \ldots , V_\mu \}$ de dimension $p$ et $n-p$ indépendantes en homologie (rationnelle), de sorte que $\lambda = b_p (M)$ et $\mu = b_{n-p} (M)$.

Si l’on suppose que le nombre $\lambda$ d’équations linéaires

$$\sum_{i=1}^\mu x_i N (C_j , V_i) =0$$

est strictement inférieur au nombre $\mu$ d’inconnues $x_i$, il existe une solution non triviale $(k_1 , \ldots , k_\mu )$. L’implication directe du théorème entraine alors que pour toute sous-variété compacte $C \subset M$ de dimension $p$, on a :

$$\sum_{i=1}^\mu k_i N(C , V_i ) =0.$$

Et il découle finalement de l’implication réciproque du théorème que la somme $\sum_i k_i V_i$ est nulle en homologie rationnelle, en contradiction avec l’indépendance linéaire des $V_i$. On a donc nécessairement $\lambda \geq \mu$.

De la même manière on a $\mu \geq \lambda$.

C.Q.F.D.

Commentaires sur la démonstration

Bien que Poincaré n’énonce « sa » dualité que dans le cas d’une variété compacte sans bord, il fait peu de doute qu’il avait remarqué que sa démonstration implique aussi le théorème suivant.

En fait --- en continuant à ignorer les trous dans la démonstration du théorème de Poincaré --- la démonstration du corollaire implique que si $(M,A)$ est une paire de variétés compactes tels que la différence $M \setminus A$ soit une variété orientable de dimension $n$, on a :

$$b_{n-p} (M \setminus A) = b_p (M, A).$$

Un cas particulier important de ce résultat est le théorème suivant qui fait le lien entre les nombres de Betti d’une sous-variété compacte $A$ de la sphère $\mathbb{S}^n$ et ceux de son complémentaire $\mathbb{S}^n \setminus A$.

Démonstration. Il suffit de remarquer que $b_{p} (\mathbb{S}^n , A)$ est égal à $b_{p-1} (A)$, sauf si $p=n$ auquel cas il faut ajouter $1$.

C.Q.F.D

Poincaré connaissait d’ailleurs certainement une incarnation bi-dimensionnelle de la dualité d’Alexander, à savoir le cas où $n=2$ et $A$ est un cercle, puisque ce cas est conséquence du théorème de Jordan selon lequel tout courbe fermée simple plongée sépare la sphère en deux composantes connexes. L’exemple, considéré par Poincaré au §6, d’un domaine de $\mathbb{R}^3$ bordé par une union disjointe de surfaces compactes suggère même que Poincaré avait au moins l’intuition du théorème général de Dualité d’Alexander.

$$ $$

Suite aux critiques de Poul Heegard, Poincaré reviendra à son théorème de dualité. C’est l’objet principal du premier complément à l’Analysis Situs. Comme nous l’expliquons dans nos commentaires la démonstration est cette fois beaucoup plus satisfaisante. Reste que l’approche géométrique initiale que nous venons de commenter a l’avantage d’être conceptuellement éclairante.

$$ $$

5. À la fin du §9 Poincaré considère le cas où $n$ est pair et $n/2$ impair, c’est-à-dire le cas où $n$ est congru à $2$ modulo $4$. Il énonce le corollaire suivant.

Pour les besoins de la démonstration, Poincaré introduit la définition suivante :

Commentaires sur la définition

La démonstration du théorème de Poincaré montre (au moins lorsque $p=1$) qu’étant donné $b_{n-p} (M)$ sous-variétés $V_i$ de dimension $n-p$ et indépendantes en homologie rationnelle, on peut trouver une base duale constituée de $b_p$ sous-variétés $C_j$ de dimension $p$ telles que la matrice $(N(C_j , V_i))$ soit la matrice identité. En particulier, si $n$ est pair, la matrice d’intersection $N$ définie ci-dessus est de déterminant $1$ et appartient donc à $\mathrm{GL} (b , \mathbb{Z} )$.

On prendra garde au fait que la matrice $N \in \mathrm{GL} (b , \mathbb{Z})$ dépend du choix des $b$ sous-variétés $V_i$. Elle est toutefois bien définie modulo la relation d’équivalence $N \sim PNP^t$ ($P \in \mathrm{GL} (b , \mathbb{Z} )$). À tout invariant d’équivalence des matrices carrées à coefficients entiers correspond donc un invariant de la variété $M$ : il suffit d’évaluer l’invariant matriciel en la matrice d’intersection $N$.

$$ $$

Démonstration. Puisque $n/2$ est impair, il découle de (3) que la matrice d’intersection est antisymétrique de taille $b \times b$. Ainsi si $b$ était impair son déterminant serait nul et on pourrait trouver des rationnels non tous nuls $k_j$ tels que $\sum_j k_j N(V_i , V_j) =0$ (pour tout $i$). Comme dans la démonstration de la dualité de Poincaré, on en déduirait que $\sum_j k_j N(C , V_j ) =0$ pour toute sous-variété compacte $C \subset M$ de dimension $n/2$, ce qui implique que la somme $\sum_i k_i V_i$ est nulle en homologie rationnelle, en contradiction avec l’indépendance linéaire des $V_i$.

Commentaires sur la démonstration

La démonstration consiste à vérifier que lorsque $n/2$ est impair la matrice $N$ est antisymétrique et non dégénérée (autrement dit symplectique). Sur n’importe quel corps contenant $\mathbb{Z}$, une telle matrice est toujours équivalente à la matrice diagonale par blocs $\mathrm{diag}\left\{ \ldots , \begin{smallmatrix} 0 & 1 \\ -1 & 0 \end{smallmatrix} , \ldots \right\}$. Sur un tel corps il n’y donc pas d’autre invariant que le rang $b$ de $N$. Nous verrons dans le prochain bloc dépliant que lorsque $n/2$ est pair, l’histoire est bien plus riche.

C.Q.F.D.

$$ $$

Commentaires sur la postérité de ce résultat

Lorsque $n/2$ est pair (cas que ne considère pas Poincaré) la matrice d’intersection $N$ est symétrique (et non dégénérée). Dans ce cas il y a d’autres invariants d’équivalence que le rang. Ainsi la parité de la matrice ($N$ est paire si tous ses éléments diagonaux sont pairs et impaire sinon), sa signature (c’est-à-dire le nombre de coefficients positifs moins le nombre de coefficients négatifs dans n’importe quelle représentation diagonale de $N$), et le fait que $N$ soit définie (c’est-à-dire que sa signature soit $\pm b$) ou non, sont tous des invariants d’équivalence ; cf. [8].

On peut ainsi voir le théorème de dualité de Poincaré comme le premier d’une longue série de résultats parmi lesquels les plus notables sont certainement les suivants :

Ces résultats, et l’étude des classes d’équivalence de matrices symétriques de $\mathrm{GL} (n , \mathbb{Z})$, permettent par exemple de construire plus de 100 millions de variétés topologiques compactes de dimension $4$, de deuxième nombre de Betti égal à $32$ et de matrice d’intersection définie, parmi lesquelles au plus 2 peuvent admettre une structure différentiable !

Remarquons finalement que, dans un registre analogue, au §13 Poincaré classifie certaines variétés de dimension 3 via l’étude des classes de conjugaison dans $\mathrm{GL} (2 , \mathbb{Z})$.

$$ $$

Poincaré conclut le §9 en notant que le résultat ci-dessus est faux si $M$ n’est pas orientable ou si $n/2$ est pair, et qu’il donnera des contre-exemples plus loin.

Commentaires sur ces contre-exemples.

Les deux contre-exemples en question sont respectivement la bouteille de Klein et le plan projectif complexe.

Noter que le corollaire généralise le fait que le premier nombre de Betti d’une surface compacte, orientable, sans bord est toujours pair. Une autre généralisation, plus profonde, de ce dernier résultat est que tous les nombres de Betti associés aux dimensions impaires d’une variété kählerienne compacte (comme par exemple une variété projective complexe non-singulière) sont pairs.

$$ $$

Commentaires sur les suites possibles de nombres de Betti de variétés

Les deux corollaires ci-dessus imposent des contraintes sur les suites possibles de nombres de Betti de variétés. Si l’on ajoute les contraintes évidentes que la suite stationne en $0$ et vaut $1$ en degré $0$ et en degré maximal, « presque » toute suite peut être obtenue. On a plus précisément le théorème suivant.

Démonstration. On peut construire de telles variétés en faisant des sommes connexes de produits de sphères. Poincaré calcule d’ailleurs les nombres de Betti de produits de sphères au §15, on peut également se référer à nos commentaires sur ce paragraphe.

C.Q.F.D.

$$ $$

Ce théorème est optimal dans le sens qu’il n’existe pas de variétés lisses dont la suite des nombres de Betti soit [13]

$$b_0 = 1 , \ b_1= \ldots = b_5 = 0 , \ b_6 = 1 ,$$

$$b_7 = \ldots = b_{11} = 0 , \ b_{12} = 1 \mbox{ et } b_k =0 \mbox{ pour } k >12.$$

Noter néanmoins qu’en général le nombre de Betti médian d’une variété de dimension divisible par $4$ peut être impair ; c’est par exemple le cas des espaces projectifs complexes de dimensions paires, comme le montre déjà Poincaré au §15, voir nos commentaires.