Commentaires sur le §15 de l’Analysis Situs (Autres modes de génération)

Dans ce paragraphe Poincaré propose de nouvelles manières de construire des variétés en combinant « le théorème des fonctions implicites », sa première définition que nous commentons ici, et les paramétrisations explicites, sa deuxième définition que nous commentons là.

On peut par exemple définir une variété $U$ de dimension $n-p+q-\lambda$ dans l’espace de dimension $n$ comme étant constituée de l’ensemble des points $x$ qui satisfont à $p$ équations $F_{\alpha} (x ; y) = 0$, où ce système d’équations dépend lui même d’un paramètre $y$ qui vit dans une variété $W$ de l’espace de dimension $q$ définie par $\lambda$ équations $\phi_\beta (y) =0$.

Ou bien, on peut définir une autre variété $V$ de dimension $q-\lambda$ dans l’espace de dimension $n$ en la paramétrant $x=(\theta_1 (y) , \ldots , \theta_n (y))$ par ces $y \in W$. Dans le cas où cette paramétrisation est globale et les fonctions $\theta_i$ sont invariante par un certain groupe discret $G$ de difféomorphismes de $W$, alors on obtient une application $W/G \to V$.

Septième exemple (Le plan projectif réel)

Soit $W=\mathbb{S}^2$ la sphère unité de $\mathbb{R}^3$ définie (implicitement) par l’équation $x^2+y^2+z^2=1$. La restriction à la sphère $W$ de l’application

$$\theta : \mathbb{R}^3 \to \mathbb{R}^6, \quad \theta (x,y,z) = (x^2 , y^2 , z^2 , xy,yz,zx)$$

(connue de nos jours sous le nom d’application de Veronese [1]) est de rang $2$ et la préimage d’un point dans $V=\theta (W)$ consiste exactement en deux points (antipodaux) dans $W$. On en déduit que $V \cong \mathbb{S}^2 / \iota $, où $\iota$ est l’involution antipodale $(x,y,z) \mapsto (-x, -y , -z)$ (qui opère sans point fixe). Ce plan projectif réel $V$ est contenu dans le sous-espace affine de dimension 5 dans $\mathbb{R}^6$ défini par la condition que la somme des trois premières coordonnées soit égale à 1. [2]

En dehors de ça, Poincaré explique que la non-orientabilité de $V$ découle du fait que l’antipode d’un point ayant pour coordonnées sphériques $(\phi , \theta )$ a quant à lui pour coordonnées $(\phi + \pi , \pi -\theta )$ et que cette transformation a un jacobien égal à -1.

$$ $$

Et les espaces projectifs réels de dimension supérieure ?

L’involution antipodale de $\mathbb{S}^3$ préserve l’orientation, ce qui correspond au fait que l’espace projectif réel de dimension 3 (le cinquième exemple de Poincaré) est une variété orientable. Plus généralement, l’espace projectif réel $\mathbb{RP}^n \cong \mathbb{S}^n / \{ \pm 1 \}$ est orientable si et seulement si $n$ est impair.

Il existe un plongement de Veronese similaire de $\mathbb{RP}^n$ dans $\mathbb{R}^{\frac{(n+1)(n+2)}{2}}$. Toutefois cette dimension est loin d’être optimale : le théorème de plongement de Whitney affirme en effet que toute variété de dimension $n$ peut être plongée dans $\mathbb{R}^{2n}$. La dimension $2n$ est optimale en général : par exemple une surface non-orientable ne peut pas être plongée dans $\mathbb{R}^3$ et pour tout $k\geq 1$, l’espace projectif réel de dimension $2^k$ ne peut pas être plongé dans $\mathbb{R}^m$, $m< 2^{k+1}$. Toutefois le problème consistant à trouver le plus petit entier $m$ tel qu’une variété donnée se plonge dans $\mathbb{R}^m$ est en général un problème difficile.

$$ $$

Huitième exemple (Carrés symétriques des sphères)

Soit $W = \mathbb{S}^{q-1} \times \mathbb{S}^{q-1}$ le produit de deux sphères de dimension $q-1$ dans l’espace $\mathbb{R}^{2q} = \mathbb{R}^q \times \mathbb{R}^q$, défini (implicitement) comme étant l’ensemble des couples $(y,z)$ vérifiant

$$y_1^2 + \ldots + y_q^2 =1 \mbox{ et } z_1^2 + \ldots + z_q^2 =1.$$

Considérons maintenant l’application $\theta = \mathbb{R}^{2q} \to \mathbb{R}^{\frac{q(q+3)}{2}}$ définie par

$$\theta (y_1 , \ldots , y_q ; z_1 , \ldots , z_q ) = (y_i+z_i ; y_i z_i ; y_i z_k + y_k z_i ).$$

Puisque la préimage d’un point dans $V=\theta (W)$ est soit un élément diagonal $(y,y)$, soit une paire de points de la forme $\{ (y,z) , (z,y) \}$, on voit que l’espace $V$ s’identifie au carré symétrique $\mathrm{Sym} (\mathbb{S}^{q-1} ) = \mathrm{Sym}^2 (\mathbb{S}^{q-1} )$ de $\mathbb{S}^{q-1}$.

Cette fois l’involution $(y,z) \mapsto (z,y)$ n’opère toutefois plus sans point fixe que sur le complémentaire de la sphère diagonale $\Sigma^{q-1} \subset \mathbb{S}^{q-1} \times \mathbb{S}^{q-1}$. A priori seule $V - \theta (\Sigma )$ est donc naturellement une variété (ouverte de dimension $2q-2$). [3] Néanmoins, pour $q\geq 3$ le lieu (possiblement) singulier $\theta (\Sigma )$ est de codimension $\geq 2$ ; on dit parfois que $V$ est une pseudo-variété.

Cas $q=2$. Poincaré détermine la nature de la singularité locale de $\mathrm{Sym} (\mathbb{S}^1 )$ au voisinage de chaque point du cercle $\theta (\Sigma )$ : considérons l’image, par l’application $\theta : \mathbb{S}^1 \times \mathbb{S}^1 \to V$

$$(y_1 , y_2 , z_1 , z_2 ) \mapsto (x_1 = y_1+z_1 , x_2 = y_2+z_2 , x_4 = y_2z_2 , x_5 = y_1z_2 + y_2z_1 ),$$

d’un petit voisinage du point diagonal $(0,1,0,1)$. On peut décrire cette image à l’aide des deux coordonnées $x_1$ et $x_2$. Pour voir cela on peut commencer par remarquer que $(y_1-z_1)^2 = x_1^2 -4x_2$ (et que $y_1+z_1 = x_1$) pour écrire $y_1$ et $z_1$ comme fonctions de $x_1$ et $x_2$. Alors les équations $y_1^2 + y_2^2 =1$ et $z_1^2 + z_2^2=1$ permettent d’écrire $y_2$ et $z_2$ en fonction de $y_1$ et $z_1$ et donc en fonction de $x_1$ et $x_2$. Puis $x_3$, $x_4$ et $x_5$, comme fonctions de $y_1$, $y_2$, $z_1$ et $z_2$ s’écrivent aussi comme fonctions de $x_1$ et $x_2$. Au final l’image d’un petit voisinage du point diagonal $(0,1,0,1)$ est difféomorphe à l’intersection d’un petit voisinage de l’origine dans les plan $x_1$, $x_2$ avec

$$\{ (x_1 , x_2 ) \in \mathbb{R}^2 \; | \; x_1^2 - 4x_2 \geq 0 \}$$

la portion du plan qui est en dessous (au sens large) de la parabole $x_1^2=4x_2$. L’espace $\mathrm{Sym} (\mathbb{S}^1 )$ est donc une surface à bord.

La surface $\mathrm{Sym} (\mathbb{S}^1 )$ est un ruban de Möbius à bord

On voit le tore $\mathbb{S}^1 \times \mathbb{S}^1$ comme le carré dont on identifie les côtés opposés par une translation. L’involution $(y,z) \mapsto (z,y)$ opère sur le carré en commutant à ces identifications. L’animation suivante montre alors que le quotient du tore par cette involution est un ruban de Möbius de bord la projection de la diagonale, égale au lieu des points fixes de l’involution.

$$ $$

Cas $q=3$. Poincaré détermine la nature de la singularité locale de $\mathrm{Sym} (\mathbb{S}^2 )$ au voisinage de chaque point de la sphère $\theta (\Sigma )$ : considérons l’intersection $\Omega$ du plan de codimension 2 de l’espace $\mathbb{R}^9$ donné par les équations $x_1 = x_3 = 0$ avec l’image, par l’application $\theta : \mathbb{S}^2 \times \mathbb{S}^2 \to V$ qui à $(y_1 , y_2 , y_3 , z_1 , z_2 , z_3 )$ associe

$$\begin{array}{l} (x_1 = y_1+z_1 , x_2 = y_1z_1 , x_3 = y_2+z_2 , x_4 = y_2z_2 , x_5 = y_1z_2 + y_2z_1 , \\ x_6 = y_3 + z_3 , x_7 = y_3z_3 , x_8 = y_1 z_3 + y_3 z_1 , x_9 = y_2 z_3 + y_3 z_2 ), \end{array} $$

d’un petit voisinage du point diagonal $(0,0,1,0,0,1)$. L’espace $\Omega$ est homéomorphe à un voisinage de l’origine dans le demi-cône

$$\{ (x_2 , x_4 , x_5 ) \in \mathbb{R}^3 \; | \; 4x_2 x_4 -x_5^2 = 0 , \ x_2 \leq 0 , \ x_4 \leq 0 \}.$$

Pour voir cela on commence par écrire $y_1=-z_1$, $y_2=-z_2$ (et donc aussi $y_3$ et $z_3$) comme fonctions de $x_2$ et $x_4$ à l’aide des équations $x_2 = -y_1^2$ et $x_4 = -y_2^2$. On vérifie ensuite que l’on obtient bien une paramétrisation bijective du demi-cône décrit ci-dessus. [4]

Une étude plus conceptuelle de la singularité

Considérons plus généralement $\mathrm{Sym} (\mathbb{S}^{q-1} )$. Décomposons l’espace $\mathbb{R}^{2q} = \mathbb{R}^q \times \mathbb{R}^q$ comme somme directe du sous-espace « diagonal » $y=z$ et de l’« anti-diagonal » $y+z=0$ :

$$\mathbb{R}^{2q} = \{ (y, y) \; | \; y \in \mathbb{R}^q \} \oplus \{ (y, -y) \; | \; y \in \mathbb{R}^q \}.$$

Sur le sous-espace anti-diagonal l’involution $(y,z) \mapsto (z,y)$ opère comme l’antipodie $(y,z) \mapsto (-y,-z)$. De là il découle que le link dans $V$, de tout point de $\theta (\Sigma )$, est le joint d’une sphère $\mathbb{S}^{q-2}$ (son link dans $\theta (\Sigma)$) et d’un espace projectif réel $\mathbb{PR}^{q-2}$ (son link dans les $q-1$ directions supplémentaires). Ce link $\mathbb{S}^{q-2}*\mathbb{RP}^{q-2}$ est, pour tout $q\geq 3$, une pseudo-variété compacte. Toutefois ce n’est jamais une variété sauf si $q=3$. En effet, si $q=3$ on a :

$$\mathbb{S}^{1}*\mathbb{RP}^{1} \cong \mathbb{S}^{1}*\mathbb{S}^{1} \cong \mathbb{S}^3.$$

Alors que si $q\neq 3$ le link $\mathbb{S}^{q-2}*\mathbb{RP}^{q-2}$ n’est pas homéomorphe à $\mathbb{S}^3$, par exemple parce qu’ils n’ont pas les mêmes groupes d’homologie. Noter que pour $q=2$,

$$\mathbb{S}^0 * \mathbb{RP}^0 = \mathbb{S}^0 * \{ \mathrm{point}\}$$

est un intervalle fermé.

Un argument similaire montre d’ailleurs que le carré symétrique $\mathrm{Sym} (M^2)$ de n’importe quelle variété $M$ de dimension 2 est une variété (de dimension 4).

$$ $$

L’espace $V= \mathrm{Sym} (\mathbb{S}^{q-1} )$ est donc une variété lorsque $q=3$, mais n’est jamais une variété lorsque $q >3$, à la différence de ce qu’affirme Poincaré. Nous verrons plus bas qu’il raisonne pourtant dessus comme s’il s’agissait toujours de variétés, en particulier en utilisant son théorème de dualité.

La variété $\mathrm{Sym} (\mathbb{S}^2 )$ est difféomorphe à $\mathbb{CP}^2$

Identifions $\mathbb{S}^2$ à la sphère de Riemann $\widehat{\mathbb{C}} = \mathbb{CP}^1$. En coordonnées complexes l’analogue de l’application $\theta$ est l’application $\theta ' : \mathbb{CP}^1 \times \mathbb{CP}^1 \to \mathbb{CP}^2$ donnée par :

$$([z_1 : z_2] , [w_1 : w_2 ]) \mapsto [z_1 w_1 : z_1w_2+z_2w_1 : z_2w_2] .$$

L’application $\theta ' $ est surjective et induit un difféomorphisme de $\mathrm{Sym} (\mathbb{S}^2)$ vers $\mathbb{CP}^2$.

De la même manière le quotient de $\mathbb{CP}^1 \times \ldots \times \mathbb{CP}^1$ ($n$ fois) par l’action du groupe symétrique $\mathfrak{S}_n$ est difféomorphe à $\mathbb{CP}^n$. Le point clé étant qu’un polynôme complexe est projectivement déterminé par ses racines.

On peut finalement remarquer que l’application $\theta : \mathbb{S}^2 \times \mathbb{S}^2 \to \mathbb{CP}^2$ est un nouvel exemple de revêtement ramifié : dans un voisinage tubulaire ($\cong \mathbb{C} \times \Sigma$) de la $2$-sphère $\Sigma$, l’application $\theta$ identifie $(z,s)$ avec $(-z,s)$ et est donc équivalente à l’application $(z,s) \mapsto (z^2 , s)$.

$$ $$

Orientabilité. En coordonnées locales l’involution $(y,z)\mapsto (z,y)$ s’écrit

$$(\phi_1 , \ldots , \phi_{q-1} ; \phi_1 ' , \ldots , \phi_{q-1} ' ) \mapsto (\phi_1 ' , \ldots , \phi_{q-1} ' ; \phi_1 , \ldots , \phi_{q-1} )$$

et son jacobien est donc égal à $(-1)^{q-1}$. On en déduit que l’involution préserve l’orientation de $\mathbb{S}^{q-1} \times \mathbb{S}^{q-1}$, et donc que $\mathrm{Sym} (\mathbb{S}^{q-1})$ est orientable, si et seulement si $q$ est impair.

Nous supposerons dorénavant que ces coordonnées locales $(\phi_1 , \ldots , \phi_{q-1})$ et $(\phi_1 ' , \ldots , \phi_{q-1} ' )$ sont des coordonnées sphériques. On note respectivement $J$ et $J'$ les éléments de volume sphérique correspondants :

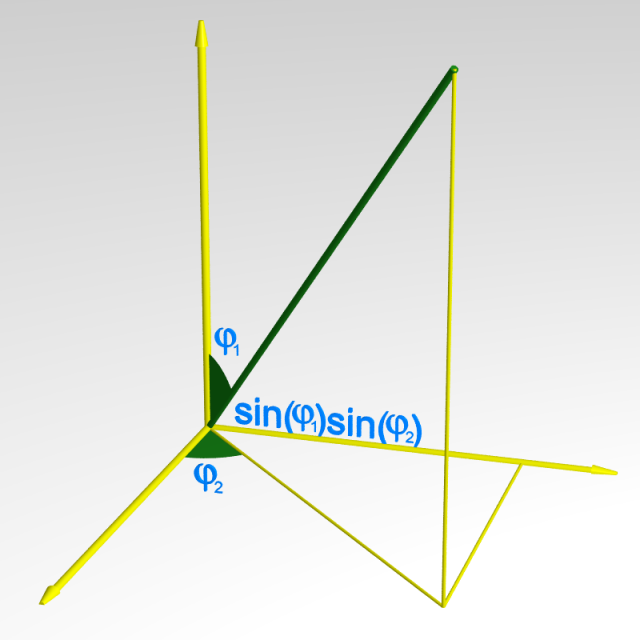
On fixe un point diagonal $(u,u)$ ainsi qu’une latitude orientée $U_1=\{ (v,u) \; | \; v \in \mathbb{S}^{q-1} \}$ et une longitude orientée $U_2=\{ (u,v) \; | \; v \in \mathbb{S}^{q-1} \}$ passant par ce point.

La proposition découle de la formule de Künneth. Nous suivons ici plutôt la démonstration de Poincaré.

Démonstration. Par dualité, il suffit de calculer les nombres de Betti en degré $\leq q-1$. De plus, toute variété de dimension strictement inférieure à $q-1$ peut être rendue disjointe de $U_1$ et $U_2$ de manière à être contenue dans

$$(\mathbb{S}^{q-1} \times \mathbb{S}^{q-1} ) - (U_1 \cup U_2 ) \cong (\mathbb{S}^{q-1} - \{ u \} ) \times (\mathbb{S}^{q-1} - \{ u \} )$$

qui est homéomorphe à une boule de dimension $2q-2$. Il ne reste plus qu’à calculer $b_{q-1}$.

Pour montrer que $U_1$ et $U_2$ sont homologiquement indépendant, Poincaré utilise la fait que pour tout nombre irrationnel $\lambda$ les périodes de la $(q-1)$-forme fermée $J_1+ \lambda J_2$ sur $U_1$ et $U_2$ sont linéairement indépendantes sur $\mathbb{Z}$.

Poincaré vérifie ensuite que toute sous-variété $\nu$ de dimension $q-1$ est homologue à $mU_1+nU_2$, où $m$, resp. $n$, est le nombre d’intersection algébrique de $\nu$ avec $U_2$, resp. $U_1$ :

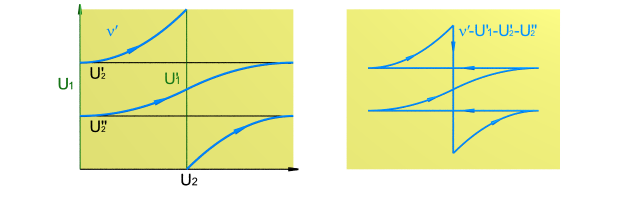
On peut supposer que $\nu$ est en position générale avec $U_1$ et $U_2$. Par chaque point d’intersection de $\nu$ et $U_1$, Poincaré fait passer un sous-espace $U_2 ' $ parallèle à $U_2$. Et par chaque point d’intersection de $\nu$ et $U_2$, il fait passer un sous-espace $U_1 ' $ parallèle à $U_1$. La somme de tous ces sous-espaces est homologue à $mU_1 + n U_2$. Par ailleurs, la sous-variété $\nu$ est homologue à une sous-variété $\nu'$ qui coïncide avec ces sous-espaces parallèles dans un petit voisinage de ces points d’intersections. Ainsi la différence entre $\nu'$ et la somme de ces parallèles est un cycle dans la boule $(\mathbb{S}^{q-1} \times \mathbb{S}^{q-1} ) - (U_1 \cup U_2 )$ et est donc homologue à zéro.

C.Q.F.D.

$$ $$

« Démonstration » de Poincaré

Les projections de $U_1$ et $U_2$ dans le quotient $V$ coïncident et définissent un $(q-1)$-cycle que nous noterons $U$. Ce cycle $U$ est non trivial en homologie : l’intégrale de la forme $J+J'$ le long de ce cycle est non-nulle.

Puis Poincaré explique que si $\nu$ est une sous-variété fermé de $V$, on peut relever $\nu$ en une sous-variété $\omega$ de $W$, en choisissant continûment, pour tout point de $\nu$, une des deux préimages de $W$. Toutefois $\omega$ n’est pas nécessairement fermée. Poincaré distingue donc deux cas.

Supposons d’abord que $\omega$ est fermée. Alors $\omega$ est homologue à 0 ou à une combinaison linéaire entière $mU_1+nU_2$ et donc $\nu$ est homologue à 0 ou à $(m+n)U$.

Supposons maintenant que $\omega$ ne soit pas fermée. Par dualité [5] il suffit de considérer les degrés $\leq q-1$. Mais alors $\partial \omega$, qui est constitué de paires de points symétriques dans $W$, est de dimension $\leq q-2$. On peut déformer, de manière symétrique, ce bord jusqu’à ce qu’il soit contenu dans la $(q-1)$-sphère diagonale $\Sigma$. Et on peut alors le remplir dans $\Sigma$. De cette manière on remplace $\nu$ par un sous-variété homologue $\nu'$ qui, elle, se relève en une sous-variété fermée $\omega'$, de sorte que le premier cas s’applique.

$$ $$

Commentaires sur cette « démonstration »

Le dernier paragraphe est douteux : comme on l’a fait remarquer, la dualité de Poincaré ne s’applique pas (au moins sans explications supplémentaires) en général ici. On peut bien sûr l’appliquer à $W$ mais il n’est pas clair que cela permette de réduire le calcul des nombres de Betti de $V$ aux degrés $\leq q-1$. Un autre problème est que Poincaré n’explicite pas la déformation utilisée dans ce paragraphe...

On peut toutefois remarquer que le double $2\nu$ de toute sous-variété fermée $\nu$ dans $V$ (ou plutôt de toute classe d’homologie...) se relève en une sous-variété fermée $\omega$ dans $W$. Cela suffit pour calculer les nombres de Betti et le résultat annoncé par Poincaré est bien correct.