Homologie

La théorie homologique représente l’une des idées majeures qui ont traversé le vingtième siècle mathématique.

Cette idée a germé dans la seconde moitié du XIX^e siècle, grâce notamment à Riemann et Betti : on devrait pouvoir mesurer la complexité d’une variété $V$ de dimension $n$ en déterminant pour chaque $p < n$ le nombre maximal de sous-variétés de dimension $p$ que l’on peut "mettre" dans $V$ sans qu’elles ne forment le bord d’une sous-variété de dimension $p+1$. La matrice de cette idée est la notion de genre [1] d’une surface. Dans l’Analysis Situs, Poincaré s’empare de cette idée, et y ajoute un ingrédient clé : on s’autorise à ajouter (formellement) les sous-variétés. Ce faisant, il donne naissance à la théorie de l’homologie. Nous retraçons cette histoire dans un article largement accessible :

• Approches de l’homologie chez Poincaré.

La présentation formelle de « la » théorie de l’homologie n’est cependant pas facile : il en existe une multitude de versions, unifiées par un cadre axiomatique, et chaque version a ses avantages et inconvénients. Nous proposons un parcours qui commence par la présentation simultanée de plusieurs versions de l’homologie (homologie polyédrale, homologie singulière) que nous appliquons à des calculs, avant de montrer que ce sont les mêmes et de développer plus avant la théorie.

Avant de nous embarquer dans cette aventure, fixons-nous quelques objectifs : nous voudrions définir un moyen d’associer à toute variété $V$ et tout entier $i$ un groupe abélien noté $H_i(V)$ (le $i$-ème groupe d’homologie de $V$) qui mesurera la « complexité topologique en dimension $i$ » de $V$. Nous voulons que ces groupes d’homologie satisfassent au moins les trois propriétés suivantes :

1. Si deux variétés sont homéomorphes, ou même homotopiquement équivalentes, alors elles ont les mêmes groupes d’homologies (naturalité).
2. Les groupes d’homologie $H_i(\{pt\})$ d’un point (ou de $\mathbb R^n$) sont $\{0\}$, sauf si $i=0$ où $H_0(\{pt\})=\mathbb Z$.
3. Les groupes d’homologie d’une union disjointe de deux variétés sont la somme directe des groupes d’homologies de chaque variété.

Ces propriétés sont loin de constituer à elles seules une liste d’axiomes caractérisant l’homologie. Nous décrirons de tels axiomes plus tard.

Des tentatives intuitives, mais semées d’embûches

Une première approche, qui reste proche de l’intuition géométrique décrite ci-dessus, consiste à suivre l’idée du bordisme. Cette approche fonctionne très bien en dimension 1 et peut servir d’introduction à l’homologie. Elle n’est toutefois pas complètement fidèle à l’esprit de Poincaré, et possède surtout un défaut majeur : en dimension plus grande, elle diffère de l’homologie. Cependant, le début de la théorie du bordisme fait une bonne introduction à l’homologie.

• Introduction à l’homologie via le bordisme.

Nous développons aussi l’approche de Poincaré. C’est principalement un « exercice de style » visant à rendre l’approche originale de Poincaré rigoureuse. Cependant, l’introduction explique les grandes idées de Poincaré et la définition que nous donnons montre l’importance d’élargir la classe des sous-variétés.

• L’homologie à la Poincaré.

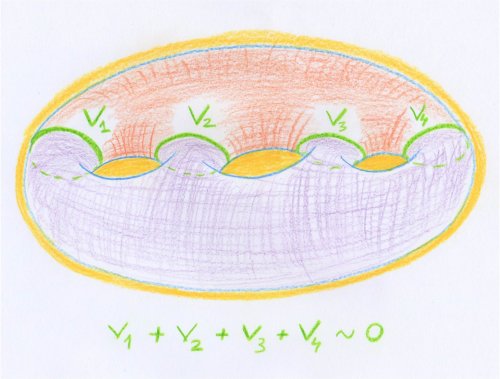
Deux définitions classiques

Nous présentons ici deux théories homologiques plus classiques. Il est important de comprendre que ces deux théories (et toutes les autres) ont chacune des avantages et des inconvénients. Telle permettra de faire des calculs assez facilement, quand telle autre sera plus facile à manier théoriquement. Ces différentes théories coexistent, et on montrera que ce sont les mêmes. Nous pouvons donc en profiter pour utiliser, devant un problème donné, la plus adaptée à ce problème.

Poincaré lui même a vu les difficultés posées par sa première définition. Le principal point délicat est de montrer que l’homologie de $\mathbb{R}^n$ est triviale. Il choisit donc, dans le premier complément, de développer une version discrète, ou combinatoire, de sa théorie. On part d’un modèle polyédral de la variété, et les sous-variétés sont des unions de facettes du polyèdre. Cette seconde approche permet de parvenir à une théorie homologique valable pour toutes les variétés lisses [2]. Cette fois les calculs des groupes d’homologie deviennent beaucoup plus faciles mais c’est la naturalité qui n’est plus évidente. Les théories homologiques modernes balancent toujours entre ces deux écueils.

• Homologies polyédrale et simpliciale.

L’Homologie singulière est la manière la plus « efficace » d’associer des groupes d’homologie à une variété topologique, ou même à n’importe quel espace topologique singulier. L’idée est de relâcher complètement la notion de sous-variété : ce sera une somme formelle d’images de simplexes par des applications continues. Cette grande souplesse rend l’étude théorique plus facile... mais les calculs à première vue plus difficiles !

• Définition de l’homologie singulière.

Avant de développer proprement la théorie, nous proposons au lecteur de suspendre son incrédulité, d’accepter momentanément que ces deux théories sont bien définies et mènent à la même homologie et de nous suivre dans la présentation de calculs d’homologie. Bien sûr, libre au lecteur de revenir plus tard là-dessus et de se précipiter sur la section d’après, qui présente l’isomorphisme des théories homologiques et le cadre axiomatique.

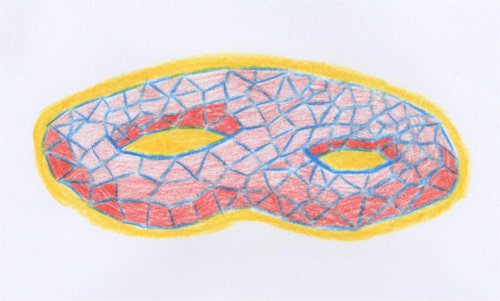
Calculs et invariants

Nous proposons donc de manipuler tout de suite l’homologie à partir des définitions, en utilisant tour à tour l’une ou l’autre et sans se préoccuper pour l’instant des problèmes de définitions. On peut commencer par calculer des exemples concrets, et l’homologie polyédrale est pour cela toute indiquée :

• Quelques calculs avec l’homologie polyédrale.

La caractéristique d’Euler-Poincaré est un invariant fondamental en topologie. Il s’agit d’un entier $\chi(X)$ associé à un polyèdre (fini) $X$ — ici encore l’approche polyédrale est plus facile. Les topologues ont l’habitude de penser à $\chi(X)$ comme « le nombre de points de $X$, à homotopie près ». Poincaré lui consacre une Note. Nous lui consacrons une rubrique qui peut se lire de manière indépendante.

• Caractéristique d’Euler-Poincaré.

Un autre résultat fondamental démontré par Poincaré dans l’Analysis Situs est le célèbre théorème de dualité , qui exprime une dualité entre les groupes d’homologie en degré $i$ et $n-i$ pour une variété compacte orientable de dimension $n$. Nous consacrons la rubrique Dualité de Poincaré à l’approche qu’en donne Poincaré dans le premier et le deuxième complément, fondée sur l’homologie polyédrale.

• Dualité de Poincaré.

Le premier groupe d’homologie d’une variété est l’abélianisé de son groupe fondamental. Ce résultat crucial, implicitement énoncé par Poincaré dans le §12 de l’Analysis Situs, permet de nombreux calculs. C’est un cas particulier d’un théorème d’Hurewicz. Nous le démontrons ici en utilisant l’homologie singulière :

• Du groupe fondamental à l’homologie en degré 1.

Avec ces résultats, il est possible de calculer l’homologie de nombreux espaces. Poincaré s’exerce sur une large famille d’espaces obtenus comme recollement de polyèdres. On retrouvera ces exemples dans la rubrique Exemples de dimension 3. Poincaré étudie en particulier divers recollements du cube pour lesquels le calcul de la caractéristique d’Euler-Poincaré permet de distinguer directement les variétés des espaces singuliers.

• Recollements du cube.
• Les suspensions d’homéomorphismes linéaires du tore.
• Variété dodécaédrique de Poincaré.

Deux outils supplémentaires permettent de calculer des groupes d’homologie : le théorème d’écrasement et surtout la suite exacte longue de Mayer-Vietoris. Nous les présentons ici dans le cadre de l’homologie singulière.

• Théorème d’écrasement et homologie des sphères. On y trouvera aussi une preuve du théorème de Brouwer et d’autres calculs.
• Suite exacte longue de Mayer—Vietoris.
• Exemples de calculs avec la suite exacte longue de Mayer—Vietoris.

Pour conclure cette rubrique de mise en pratique, on peut citer deux classes d’exemples supplémentaires. D’une part, on peut étudier un autre exemple de dimension 3, les sphères de Brieskorn, où on utilise la suite exacte longue pour le calcul de l’homologie. Le second est de dimension 4, lié aux surfaces complexes.

• Homologie des sphères de Brieskorn.
• Homologie des fibrations de Lefschetz.

Isomorphismes des théories homologiques

Il s’agit maintenant de montrer que les différentes théories présentées sont effectivement les mêmes. Cela justifiera a posteriori les calculs effectués précédemment, qui utilisaient à la fois l’homologie polyédrale (dont le fait qu’elle soit bien définie pour une variété n’est pas encore clair) et l’homologie singulière. Mais avant cela, présentons tout de même une dernière théorie homologique : l’homologie cellulaire, plus difficile à définir. Elle vient logiquement après l’homologie singulière [3] et s’applique à une catégorie particulière d’espaces topologiques (qui contient les variétés) appelés CW-complexes. L’homologie cellulaire permet de faire le lien entre homologie polyédrale et homologie singulière et s’avère très pratique pour faire des calculs.

• L’homologie cellulaire.

On pourrait ajouter encore d’autres théories homologiques, comme par exemple celle introduite par Čech.

Pour montrer les isomorphismes entre les différentes théories homologiques, on peut les comparer deux à deux en utilisant l’homologie singulière comme pivot :

• Comparaison des homologies simpliciale et singulière.
• Comparaison des homologies cellulaire et singulière.
• Comparaison entre les homologies à la Poincaré et singulière. (Cette rubrique est plus longue et constitue en grande partie un exercice de style. Elle introduit différentes théories homologiques intermédiaires.)

Une autre approche est l’approche axiomatique déjà mentionnée. Il faut commencer par des rudiments d’algèbre homologique, qui formalise les notions de complexes de chaînes et de cochaînes et définit le cône d’un morphisme de complexes. On peut ensuite décrire les axiomes et prouver l’unicité d’une théorie homologique.

• Complexes de (co)chaînes et (co)homologie.
• Lemme des cinq et naturalité de la suite exacte longue en (co)homologie.
• Cône d’un morphisme de complexe de (co)chaînes.
• Axiomes d’une théorie des chaînes pour les espaces topologiques.

Cohomologie

Nous avons vu apparaître deux fois une notion de dualité : d’une part dans la dualité de Poincaré et d’autre part dans les constructions d’algèbre homologique. Il est temps d’introduire et d’étudier la cohomologie. On trouvera dans cette rubrique une autre démonstration de la dualité de Poincaré (dans une version plus générale). On y introduit aussi la cohomologie de De Rahm, à l’aide de formes différentielles.

• Cohomologie.

(Co)Homologie à coefficients

Il est possible de changer les coefficients dans lesquels on calcule l’homologie, et de passer à des groupes abéliens plus généraux. Cette construction est expliquée en homologie singulière :

• Homologie à coefficients dans d’autres groupes.

La construction précédente utilise une version grandement généralisée de la dualité de Poincaré, prenant en compte les coefficients :

• Théorème des coefficients universels.

En guise de conclusion

Après ce long parcours, on peut-être tenté de revenir à l’intuition initiale et de se poser la question suivante : un cycle en homologie peut-il être représenté par une sous-variété ? le produit d’intersection a-t-il une interprétation géométrique ? C’est l’objet de travaux (difficiles) de René Thom, que nous présentons ici :

• Interprétation géométrique du produit d’intersection.
• Réalisation des classes d’homologie par des sous-variétés.

Nous avons donné un premier aperçu du théorème de Witold Hurewicz sur les liens entre l’homologie et l’homotopie. Nous décrivons plus complètement ce théorème :

• Lien entre homologie et homotopie : le théorème d’Hurewicz.

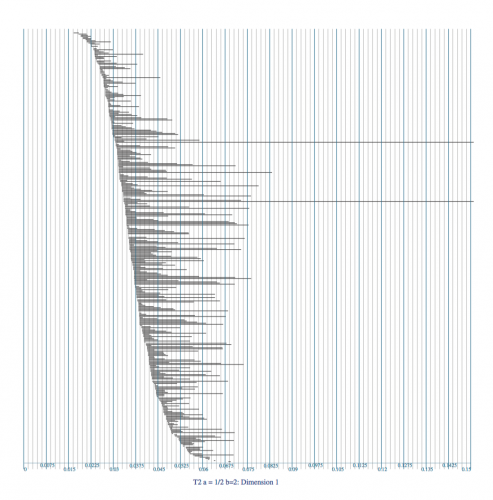
Nous proposons aussi une ouverture sur la vivacité de la théorie de l’homologie, à travers l’homologie persistante :

• Une invitation à l’homologie persistante.