Homologie des fibrations de Lefschetz

Dans cet article, nous expliquons comment calculer les nombres de Betti d’une surface algébrique complexe admettant une fibration de Lefschetz. Observons dès maintenant que le cas d’une surface algébrique complexe quelconque s’en déduit. En effet, comme nous l’avons expliqué ici, toute surface algébrique complexe admet un pinceau de Lefschetz. Après éclatement des points bases du pinceau, on obtient une surface complexe munie d’une fibration de Lefschetz (voir la fin de cet article). Par ailleurs, l’effet d’un éclatement sur les nombres de Betti est bien connu : comme expliqué ici, le nombre de Betti $b_2$ augmente d’une unité, et les autres restent inchangés. Ainsi, pour calculer les nombres de Betti d’une surface algébrique complexe quelconque, il suffit donc de savoir le faire pour une surface qui admet une fibration de Lefschetz.

On considère donc une surface algébrique complexe connexe $X$, munie d’une fibration de Lefschetz $f : X \rightarrow \mathbb P^1(\mathbb C)$. On notera $n$ le nombre de fibres singulières de la fibration, et $g$ le genre d’une fibre régulière de $f$. On fixera également une fibre régulière $F$ de la fibration et on notera $\gamma_1, \ldots, \gamma_n$ les cycles évanescents dans $F$ comme dans le calcul du Groupe fondamental d’une fibration de Lefschetz.

Expliquons un peu la stratégie. A priori, il y a cinq nombres de Betti à déterminer : $b_0(X)$, $b_1(X)$, $b_2(X)$, $b_3(X)$ et $b_4(X)$. Cependant, comme $X$ est connexe, orientable et fermée, on sait que $b_0(X)$ et $b_4(X)$ sont égaux à $1$. Par ailleurs, par dualité de Poincaré, les nombres $b_3(X)$ et $b_1(X)$ sont égaux. Enfin, on a déjà expliqué ici comment calculer le groupe fondamental de $X$, et on devrait pouvoir en déduire $b_1(X)$ via le théorème de d’Hurewicz. Il reste donc essentiellement à déterminer $b_2(X)$. Le calcul direct n’est pas évident [1]. Par contre, comme bien souvent, il est relativement facile de trouver la caractéristique d’Euler-Poincaré de $X$. Comme cette dernière est égale à la somme alternée des nombres de Betti de $X$, ceci permettra de déduire $b_2(X)$ des autres nombres de Betti.

Calcul de la caractéristique d’Euler-Poincaré

On commence par calculer la caractéristique d’Euler-Poincaré de $X$. On considère des petits disques deux à deux disjoints $D_1, \ldots, D_n\subset \mathbb P^1(\mathbb C)$ autour de chaque point critique de $f$, et on note $\Delta$ le complémentaire de l’union des intérieurs de ces $n$ disques dans $\mathbb P^1(\mathbb C)$. On note

$$V_i = f^{-1} (D_i)\quad\quad\mbox{et}\quad\quad V = f^{-1} (\Delta) .$$

La caractéristique d’Euler-Poincaré est additive : elle vérifie $\chi(A\cup B)=\chi(A)+\chi(B)-\chi(A\cap B)$. De plus, la dualité de Poincaré implique que la caractéristique d’Euler-Poincaré de toute variété fermée de dimension impaire est nulle (voir ici). Ainsi, si $A$ et $B$ sont deux variétés compactes à bord de dimension 4, recollées sur leur bord, on aura $\chi(A\cup B)=\chi(A)+\chi(B)$. En particulier, la caractéristique d’Euler-Poincaré de notre surface complexe $X$ satisfait

$$\chi(X)=\chi(V)+\sum_{i=0}^n\chi(V_i).$$

La variété $V$ est un fibré de fibre $F$ et de base $\Delta$. La caractéristique d’Euler-Poincaré étant multiplicative par fibration (voir ici), on a $\chi(V)=\chi(F)\chi(\Delta)$. Par définition, $\Delta$ est la droite projective complexe $\mathbb{P}^1(\mathbb{C})$ privée de $n$ disques deux à deux disjoints ; on a donc $\chi(\Delta)=2-n$. La fibre $F$ est quant à elle une surface fermée connexe de genre $g$ ; on a donc $\chi(F)=2-2g$. On obtient donc

$$\chi(V)=(2-2g)(2-n).$$

Comme expliqué au début de cet article, chaque fibre singulière de $f:X\to \mathbb{P}^1(\mathbb{C})$ s’obtient (à homéomorphisme près) en partant de la fibre régulière $F$, et en « pinçant un cycle évanescent ».

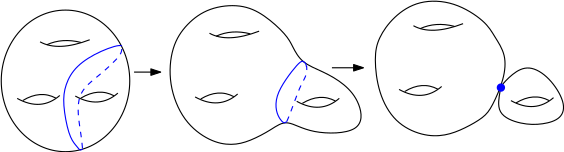
Déformation d’une fibre régulière en une fibre singulière. En bleu, le cycle évanescent qui dégénère sur un point double ordinaire.

Cela revient à ôter à $F$ un anneau, puis à coller sur les deux cercles bords ainsi créés deux disques qui ne se touchent qu’en leur centre. Par additivité, la caractéristique d’Euler-Poincaré d’une fibre singulière est donc égale à celle de $F$, moins celle d’un anneau, plus deux fois celle d’un disque, moins celle d’un point, c’est-à-dire $(2-2g)-0+2\times1-1=3-2g$. Comme $V_i$ se rétracte par déformation sur sa fibre singulière (voir Groupe fondamental des fibrations de Lefschetz), et comme la carcatéristique d’Euler-Poincaré est invariante par homotopie, on obtient donc

$$\chi (V_i) = 3-2g.$$

Le lecteur pourra aussi redémontrer ceci en utilisant la description des variétés $V_i$ par attachement d’une anse d’indice deux sur le produit $D \times F$ qui est décrit dans Reconstruction topologique des fibrations de Lefschetz.

En mettant tout bout à bout, on obtient la caractéristique d’Euler-Poincaré de $X$ :

$$\chi(X)=4-4g+n.$$

Calcul des nombres de Betti

On peut maintenant déterminer les nombres de Betti de $X$.

Le nombre de Betti $b_0(X)$ est égal au nombre de composantes connexes de $X$. On sait également que $H_4(X)$ est isomorphe à $\mathbb{Z}$, engendré par la classe fondamentale de $X$. Ainsi,

$$b_0(X)=b_4(X)=1.$$

Dans un autre article, nous avons montré que le groupe fondamental [2] de $X$ est égal au quotient $\pi_1(X)=\pi_1(F)/N$ du groupe fondamental de la fibre régulière $F$ par le sous-groupe distingué $N$ engendré par des représentants des cycles évanescents $\gamma_1,\dots,\gamma_n$. En appliquant le théorème d’Hurewicz, on en déduit aussi la formule

$$H_1(X,\mathbb{Z})=H_1(F,\mathbb{Z})/\langle [\gamma_1],\ldots,[\gamma_n]\rangle$$

où $[\gamma_i]$ désigne la classe d’homologie de la courbe $\gamma_i$. Notons $k$ le rang de la famille $([\gamma_i])_{i=1,\ldots,n}$ dans l’espace vectoriel $H_1(F,\mathbb{R})$. L’égalité ci-dessus implique que l’on a

$$b_1(X)=\dim H_1(F,\mathbb{R})-k=2g-k.$$

Puisque $X$ est fermée, orientable (comme toute variété algébrique complexe) et connexe, la dualité de Poincaré implique que

$$b_3(X)=b_1(X).$$

Enfin, on sait que la caractéristique d’Euler-Poincaré de $X$ est égale à la somme alternée ses nombres de Betti, et on a montré ci-dessus qu’elle vaut $4-4g+n$. On a donc

$$b_0(X)-b_1(X)+b_2(X)-b_3(X)+b_4(X)=4-4g+n.$$

Nous avons ainsi montré les formules suivantes que l’on trouve dans le Quatrième Complément à l’Analysis Situs :

$$b_0(X)=b_4(X)=1,\quad b_1(X)=b_3(X)=2g-k,\quad b_2(X)=2+n-2k.$$

Exemples

À titre de vérification, supposons que $X=\mathbb{P}^1(\mathbb{C}) \times F$, à savoir, il n’y a aucune singularité $n=0$ et donc aussi $k=0$. On a alors $b_2(X)=2$ ce qui est compatible avec la formule de Künneth

$$H_2(X,\mathbb{R})=H_2(\mathbb{P}^1(\mathbb{C}),\mathbb{R})\otimes H_0(F,\mathbb{R})\oplus H_0(\mathbb{P}^1(\mathbb{C}),\mathbb{R})\otimes H_2(F,\mathbb{R}).$$

Prenons maintenant l’exemple du Pinceau de cubiques de Hesse : on a 4 fibres singulières contenant chacune 3 singularités ($n=4\times 3=12$), une fibre générique qui est un tore ($g=1$) et un premier nombre de Betti nul ($k=2g=2$). On en déduit $b_2(X)=10$. Ceci est bien compatible avec la description de $X$ comme le plan projectif complexe éclaté en 9 points : en effet, on a $b_2(\mathbb{P}^2(\mathbb{C})=1$, et chaque éclatement rajoute 1 au deuxième nombre de Betti (il s’agit de la classe fondamentale du diviseur exceptionnel ; voir notre article sur les éclatements).

Dans l’article Reconstruction topologique d’une fibration de Lefschetz, nous allons un peu plus loin que le simple calcul des nombres de Betti de $X$ : nous décrivons une construction géométrique de tous les cycles de $X$.