
|
> Surfaces complexes > Groupe fondamental des fibrations de Lefschetz Groupe fondamental des fibrations de Lefschetz |
Ce bloc est consacré au calcul du groupe fondamental des fibrations de Lefschetz. Il fait suite au bloc La formule de Picard-Lefschetz, dont nous reprendrons ici les notations. Rappelons que nous y avons notamment montré la formule de Picard-Lefschetz, qui affirme que lorsqu’une fibre régulière de la fibration effectue un tour positif autour d’une fibre singulière, la monodromie correspondante est représentée par un twist de Dehn à droite associé à une classe d’isotopie de courbe fermée simple contenue dans la fibre régulière, qui est appelée un cycle évanescent.
Une propriété "orthogonale" des cycles évanescents est la suivante : lorsque la fibre régulière tend vers la fibre singulière (par exemple de façon radiale) le cycle évanescent est pincé vers le point singulier de la fibre singulière, ainsi que le montre la figure.
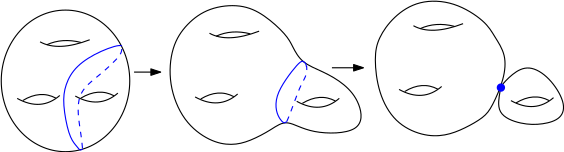
- Déformation d’une fibre régulière en une fibre singulière. En bleu, le cycle évanescent qui dégénère sur un point double ordinaire.
Nous encourageons le lecteur à montrer ce phénomène, en utilisant le modèle du voisinage tubulaire de la fibre singulière expliqué dans la démonstration de la Formule de Picard-Lefschetz. Ceci explique de façon convaincante pourquoi les cycles évanescents sont nuls dans le groupe fondamental de $X$.
Nous montrons maintenant une variation de ce fait, qui permet de rétracter par déformation un voisinage de la courbe singulière sur cette dernière. Attention la rétraction ne préserve pas la fibration, c’est donc un procédé un peu différent de ce qui est représentée sur la figure ; d’ailleurs ce n’est pas possible de construire une rétraction qui préserve également la fibration, ce que nous soumettons comme exercice au lecteur comme application de la formule de Picard-Lefschetz.
Soit $f : X \rightarrow \mathbb D$ une fibration de Lefschetz ayant une unique fibre singulière au dessus de l’origine. Il existe une rétraction par déformation $\{ r_t \}_{t\in [0,1]}$ de $X$ sur $F_0$. De plus, il existe un anneau $A \subset F_{z_0}$ isotope au cycle évanescent, qui est contracté sur le point critique de $f$ par $r_1$, et tel que $r_1$ exerce un difféomorphisme de $F_{z_0} \setminus A$ sur $F_0 \setminus C(f)$.
On fixe $\eta_0 >0$ et on définit une rétraction $\{ r_t \} _{0\leq t \leq 1} $ par
$$ r_t (x,y) = (x, (1-t) y) \text{ si } (x,y)\in \partial \mathbb D \times \mathbb D_{\eta_0}$$
et
$$ r_t (x,y) = ( (1-t) x, y) \text{ si } (x,y)\in \mathbb D_{\eta_0} \times\partial \mathbb D.$$
Par le principe d’Ehresman, si $\eta _0$ est suffisamment petit, cette rétraction se prolonge en une rétraction $\{ r_t\} _{0\leq t\leq 1} $ de $f^{-1} (\mathbb D_{\eta_0} ) \setminus U$ sur $F \setminus U$.
(en fait, ici on peut faire en sorte que cette rétraction relève la rétraction radiale $z\mapsto (1-t) z$ sur $\mathbb C$, mais ce ne sera plus possible dans ce qui suit)
Il nous reste à prolonger cette rétraction sur $U \cap f^{-1} (\mathbb D_{\eta_0})$. Pour cela, on choisit $\eta_0$ suffisamment petit pour que
$$ U \cap f^{-1} (\mathbb D_{\eta_0} ) \subset D = (\mathbb D \times \mathbb D _{1/4} ) \cup ( \mathbb D _{1/4} \times \mathbb D ) ,$$
ainsi qu’une fonction continue $\phi: D\setminus \{ (0,0) \}\rightarrow [0, 1]$ de sorte que
- $\phi>0$ si $|x|> |y|$
- $\phi = 0$ si $|x|\leq |y| $
- $\phi = 1$ si $|y|= 0$
- $\phi=1$ sur $\{ |x|\geq 1/2 \text{ et } |y|\leq 1/4 \}$
Le fait que cette fonction existe est d\^u au fait que le domaine $\{ |x| \geq 1/2 \text{ et } |y|\leq 1/4\}$ n’intersecte pas la diagonale. On définit alors $ \psi (x,y) = \phi (y,x)$, de sorte que les propriétés analogues soient satisfaites pour $\psi$ après avoir permuté les coordonnées $x$ et $y$, et on pose
$$ \phi_t= 1-t + t \phi \text{ et } \psi_t = 1-t + t \psi $$
et
$$ r_t (x,y) = (\phi_t x, \psi_t y) .$$
Les applications $r_t $ pour $t\in [0,1]$ s’étendent par continuité en l’origine $(0,0)$, et prolongent notre rétraction dans $U\cap f^{-1} (\mathbb D_{\eta_0})$.
C.Q.F.D.
Soit $f: X \rightarrow \mathbb P^1(\mathbb C)$ une fibration de Lefschetz. Alors $X$ est connexe ssi les fibres de $f$ sont connexes.
C.Q.F.D.
Soit $f: X\rightarrow \mathbb P^1(\mathbb C)$ une fibration de Lefschetz avec $X$ connexe. Pour tout $z_0 \in \mathbb P^1(\mathbb C) \setminus VC(f)$, l’application
$$\pi_1 (F_{z_0}) \rightarrow \pi_1(X)$$
est surjective, et son noyau est le sous-groupe normal engendré par les classes de conjugaison associées aux cycles évanescents.
$$1 \rightarrow \pi_1 ( F_0,Z_0) \rightarrow \pi_1 (f^{-1}(\overline{D_0}),Z_0) \rightarrow \pi_1 (\overline{D_0},z_0) \rightarrow 1 $$
Le groupe $\pi_1(\overline{D_0},z_0)$ admet la présentation
$$ \pi_1(\overline{D_0}, z_0) = < t_1,\ldots, t_r\ |\ t_1\ldots t_r= 1 >. $$
C’est en particulier un groupe non abélien libre, ce qui nous permet de voir que $\pi_1(f^{-1}(\overline{D_0}))$ est un produit semi-direct de $\pi_1(\overline{D_0})$ sur $\pi_1(F_0)$, twisté par une action
$$\tilde{m} : \pi_1(\overline{D_0}) \rightarrow \text{Aut} (\pi_1(F_0)) $$
qui relève $m$. Les automorphismes $\tilde{m} (t_k)$ sont au niveau homotopique induits par un twist de Dehn à droite qui fixe le point base de $F_{z_0}$, le long d’un cycle évanescent $\gamma_k \subset F_{z_0}$. Au dessus de $t_k$, la fibration $f$ est donc un fibré en surfaces dont le groupe fondamental est
$$ \pi_1 (f^{-1} (t_k), Z_0) \simeq \mathbb Zt_k \times_{\tilde{m}(t_k)} \pi_1(F_0, Z_0) $$
Le complément à la formule de Picard-Lefschetz, nous enseigne que l’application
$$ \pi_1 (f^{-1} (t_k), Z_0) \simeq \mathbb Z t_k \times_{\tilde{m}(t_k)} \pi_1(F_0, Z_0) \rightarrow \pi_1 (f^{-1} (\overline{D_k}) , Z_0) \simeq \pi_1(F_{z_k})$$
a pour noyau le sous-groupe normal engendré par $t_k$ et par la classe de conjugaison du cycle évanescent $\gamma_k$. Le théorème de Van Kampen conclut la démonstration.
C.Q.F.D.

