
|
> Surfaces complexes > La formule de Picard-Lefschetz La formule de Picard-Lefschetz |
Dans cet article nous nous intéressons à la monodromie des fibrations de Lefschetz. Les concepts que nous allons discuter s’appliquent donc tout aussi bien à l’étude des pinceaux de Lefschetz, quitte à éclater la surface ambiante sur l’ensemble des points bases du pinceau. Nous renvoyons (même si cela n’est pas strictement nécessaire) à l’article Pinceaux et fibrations de Lefschetz, où le lecteur trouvera les définitions formelles et plusieurs exemples de constructions de fibrations de Lefschetz. Voir aussi l’article Pinceau des cubiques de Hesse.
Introduction à la monodromie
Donnons nous une fibration de Lefschetz ainsi qu’un cycle $c \in H_1 (F, \mathbb Z)$ dans le premier groupe d’homologie d’une fibre régulière $F$ de la fibration. Faisons maintenant bouger la fibre régulière de façon continue et supposons que l’on revienne à notre fibre régulière originale. Si au cours du mouvement la fibre n’est jamais devenue singulière, alors on peut déformer le cycle $c$ "continûment" et lorsqu’on revient à notre position originale, le cycle $c$ deviendra un cycle $c' \in H_1(F,\mathbb Z)$. La transformation $c \mapsto c'$ est appelée la monodromie : il s’agit en fait d’un isomorphisme linéaire qui préserve la forme d’intersection sur $H_1(F, \mathbb Z)$. Si l’on note $\pi_1$ le groupe fondamental de la base privée des valeurs critiques de la fibration de Lefschetz, on définit de cette façon une représentation de $\pi_1$ dans le groupe des automorphismes de $H_1(F, \mathbb Z)$ qui préservent la forme d’intersection.
$\delta \rho \omicron \mu \omicron \varsigma $ veut dire route en grec, monodrome se traduit donc littéralement par "le fait de ne pouvoir se déplacer qu’en ligne droite". On fait donc une erreur ici, en appelant monodromie la représentation qui s’oppose au phénomène de monodromie.
Regardons un exemple pour comprendre ce qui se passe avec un point de vue analytique, pour ceux qui ne seraient pas (encore ?) convaincus pas les méthodes de l’Analysis Situs. Considérons donc le pinceau de courbes elliptiques $\{ E_\lambda \}_\lambda$ qui sont définies en coordonnées affines $(x,y)$ par les équations
$$ y^2 = x (x-1) (x-\lambda) , $$
où $\lambda$ est un nombre complexe que l’on supposera différent de $0$, $1$ pour que $E_\lambda$ soit non singulière. On rajoute un point à l’infini à $E_\lambda$ de façon à ce que $E_\lambda$ soit une courbe compacte de genre $1$. Dans la vidéo
on montre que la courbe $E_\lambda$ est de façon tout à fait explicite biholomorphe au quotient de $\mathbb C$ par le réseau $\mathbb Z a_\lambda + \mathbb Z b_\lambda$, où $a_\lambda$ et $b_\lambda$ sont les nombres complexes définis par les intégrales elliptiques
$$ a_\lambda = 2 \int_0 ^1 \frac{dx}{\sqrt{x(x-1)(x-\lambda)}}$$
et
$$b_\lambda = 2 \int _1^\lambda \frac{dx}{\sqrt{x(x-1)(x-\lambda)}}$$
Le groupe $H_1(E_\lambda, \mathbb Z)$ s’identifie donc ici à $\mathbb Z a_\lambda + \mathbb Z b_\lambda$. Lorsque l’on fait subir à $\lambda$ un lacet partant de $\lambda_0$ qui revient à sa position originale, tout en évitant les valeurs singulières $0$ et $1$, les nombres $a_{\lambda_0}$ et $b_{\lambda_0}$ auront été changés en des nombres $a_{\lambda_0} ' = \alpha a_{\lambda_0} + \beta b_{\lambda_0}$ et $b_{\lambda_0} '= \gamma a_{\lambda_0} + \delta b_{\lambda_0}$ où
$$\left( \begin{array}{cc} \alpha & \beta \\ \gamma & \delta \end{array} \right)$$
est une matrice du groupe $SL_2(\mathbb Z)$. La représentation $\pi_1(\mathbb C \setminus \{ 0, 1 \}, \lambda_0)$ dans $SL_2(\mathbb Z)$ ainsi obtenue a pour image le groupe $\Gamma_2$ des matrices congrues à l’identité modulo $2$. En travaillant un peu sur les intégrales elliptiques, on peut montrer que les fonctions $a_\lambda$ et $b_\lambda$ vérifient en fait l’équation différentielle du second ordre suivante
$$ \lambda (\lambda-1) \frac{d^2 c}{d\lambda^2 } + (2\lambda-1) \frac{dc}{d\lambda} + \frac{c}{4} = 0$$
appelée équation de Picard-Fuchs. Nous renvoyons au magnifique livre de Clemens [1]. Rien d’étonnant donc à ce que ses solutions soient multiformes ! Pensez par exemple à la fonction multiforme $\log \lambda$ qui vérifie l’équation (plus simple) $\lambda \frac{dc}{d\lambda}-1= 0$. Picard, contemporain de Poincaré, a considérablement généralisé ces résultats, notamment à des pinceaux de courbes de genre quelconque, et même dans le cadre d’intégrales multiples sur des surfaces complexes. Mais c’est une autre histoire...
De l’homologie à l’homotopie
Dans le Troisième Complément de l’Analysis Situs, Poincaré fait le saut conceptuel qui consiste à remplacer la "simple" donnée d’un cycle dans une fibre, par un objet encore plus géométrique, comme par exemple celle d’une classe d’isotopie de lacet. Il démontre en fait que l’on peut suivre continûment l’ensemble des points d’une même fibre le long d’une déformation de cette dernière, et que le résultat est essentiellement unique à isotopie près. Son argument fait intervenir des coupures et ses fonctions Fuchsiennes [2]. Nous allons utiliser une technique beaucoup plus simple, dûe à Ehresman, et qui ne repose pas sur la connaissance précise de la topologie des fibres. [3]
Formalisons un peu ! Donnons nous une fibration de Lefschetz $f: X\rightarrow \Sigma$, qui est par définition une application holomorphe propre d’une surface complexe à valeurs dans une surface de Riemann $\Sigma$, et qui n’a que des points critiques non dégénérés, au plus un seul apparaissant dans une même fibre. Nous renvoyons à notre article Pinceaux et fibrations de Lefschetz pour une présentation plus approfondie dans le cas où $\Sigma = \mathbb P^1(\mathbb C)$.
Pour tout $z$ dans $\Sigma$, on note $F_z = f^{-1} (z) \subset X$ la fibre au dessus de $z$. On note également $C(f)\subset X$ et $VC(f)= f(C(f))\subset \Sigma$ respectivement les ensembles des points critiques et des valeurs critiques de $f$. Ce sont des ensembles discrets de $X$ et $\Sigma$ respectivement. Les fibres $F_z$ pour $z\in VC(f)$ sont singulières, mais en vertu du lemme de Morse holomorphe (voir Pinceaux et fibrations de Lefschetz), elles admettent une unique singularité qui est un point double ordinaire. La terminologie “fibration de Lefschetz” est donc ambiguë de ce point de vue. Par contre, la restriction
$$f'= f_{|X'} : X' = X \setminus f^{-1} (VC(f)) \rightarrow \Sigma' = \Sigma\setminus VC(f) $$
est une fibration différentiable au sens classique du terme :
Pour toute valeur régulière $z$ de $f$, il existe un voisinage $V $ de $z$ au dessus duquel la fibration est un produit, c’est à dire qu’il existe un difféomorphisme $\Phi$ de $V \times F_z$ dans $f^{-1}(V)$ tel que $f\circ \Phi$ est la projection de $V\times F_z$ dans $V$.
On dira que $\Phi$ est une trivialisation de la fibration $f$ au dessus de $V$. Attention, ici la trivialisation ne pourra pas être choisie de façon holomorphe, car en général le module des courbes $F_z$ variera avec $z$ (c’est le cas par exemple s’il existe des fibres singulières).
On fixe un point base $z_0 \in \Sigma'$. Soit $\text{Mod}^+ (F_{z_0})$ le groupe des classes d’équivalence d’homéomorphismes préservant l’orientation de $F_{z_0}$ modulo la relation d’isotopie (voir l’article Autour du groupe modulaire des surfaces). La monodromie de la fibration $f '$ est une représentation
$$m : \pi_1 ( \Sigma', z_0) \rightarrow \text{Mod}^+(F_{z_0})$$
à valeurs dans le groupe modulaire de $F_{z_0}$.
Elle est définie comme suit : si $\gamma : [0,1] \rightarrow \Sigma'$ est un lacet vérifiant $\gamma(0)= \gamma(1)= z_0$, on considère une famille d’homéomorphismes $\psi_t : F_{\gamma(0)= z_0} \rightarrow F_{\gamma(t)}$ qui dépendent continûment de $t$. On montre alors :
![]() que la famille $\{\psi_t\}_{t\in [0,1]}$ existe,
que la famille $\{\psi_t\}_{t\in [0,1]}$ existe,![]() que $\psi _1$ est un homéomorphisme de $F_{z_0}$ qui est bien défini à isotopie près, et enfin
que $\psi _1$ est un homéomorphisme de $F_{z_0}$ qui est bien défini à isotopie près, et enfin ![]() qu’il ne dépend que de la classe d’homotopie de $\gamma$.
qu’il ne dépend que de la classe d’homotopie de $\gamma$.
Ces trois propriétés sont très faciles à établir à partir du lemme d’Ehresmann, nous les laissons en exercice au lecteur. Elles permettent notamment de définir
$$m([\gamma]) := [\psi_1 ] \in \text{Mod} ^+ (F_{z_0})$$
pour toute classe d’homotopie $[\gamma]\in \pi_1(\Sigma' , z_0)$.
Si la courbe $\gamma$ est simple, la pré-image de $\gamma$ par $f$ dans $X$ est une variété de dimension $3$ qui est un fibré en surfaces au dessus du cercle. L’élément $m(\gamma)$ est la monodromie de ce fibré, voir notre article Fibrés sur le cercle.
Monodromie autour des fibres singulières
On note $\mathbb D := \{ z\in \mathbb C \ |\ |z|<1 \}$ le disque unité.
Soit $f: X \rightarrow \mathbb D$ une fibration de Lefschetz au dessus du disque unité ayant une seule fibre singulière au dessus de l’origine. Alors la monodromie de $f'$ correspondant à un élément de $\pi_1(\mathbb D^*,z_0)$ faisant un tour de l’origine dans le sens direct est un twist de Dehn à droite.
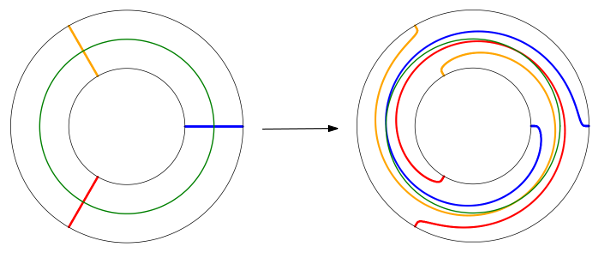
- Twist de Dehn à droite
Un twist de Dehn à droite est associé à une courbe fermée simple $\gamma \subset F_{z_0}$. Regardons l’action de ce twist de Dehn sur les classes d’isotopie de courbes fermées. Une telle classe contient une courbe $c$ qui est transverse à $\gamma$. Formons une nouvelle courbe fermée de la façon suivante : elle est construite en gardant la courbe $c$ entre les moments où elle intersecte $\gamma$, et à chaque fois que $c$ rencontre $\gamma$, elle fait un tour de $\gamma$ en partant sur la droite, avant de repartir dans la courbe $c$ à l’endroit on on s’était arrêté. On montre que la classe d’isotopie de cette nouvelle courbe ne dépend que de la classe d’isotopie de la courbe $c$ : il s’agit de l’image de $c$ par le twist de Dehn à droite associé à $\gamma$. Nous renvoyons à l’article Autour du groupe modulaire des surfaces, où le lecteur pourra trouver des informations complémentaires et des références intéressantes.
Pour ceux qui préfèrent les formules, si $A \simeq [0, 1] \times \mathbb S^1 \subset F_{z_0}$ est un anneau dans lequel la courbe $\gamma $ est l’âme définie par $1/2\times \mathbb S^1$, le twist de Dehn à droite est représenté par le difféomorphisme $\Phi $ de $F_{z_0}$ qui est l’identité à l’extérieur de $A$, et qui dans $A$ est donné par $\Phi (t, \zeta ) = (t, \zeta \exp (-2i\pi t))$.
Notons que l’on peut définir aussi la notion de twist de Dehn à gauche. La composée de deux tels twists le long d’une même courbe fermée simple est isotope à l’identité.
La démonstration de la formule de Picard-Lefschetz que nous proposons consiste à décrire la structure des voisinages tubulaires des fibres singulières. Avant d’étudier le cas général, nous conseillons vivement au lecteur de visionner la vidéo suivante, dans laquelle est traité le cas des fibrations par courbes hyperelliptiques, et le lien avec une certaine représentation à valeurs dans le groupe des tresses.
Nous ferons usage du concept suivant : étant donné un point quelconque $z\in \Sigma$, et un domaine compact $D \subset F _z $, une déformation de $D$ dans les fibres voisines est la donnée d’un voisinage $V$ de $z$ dans $\Sigma $, et d’un plongement $\Phi : V \times D \rightarrow X$, tel que $\Phi( z, \cdot) = id_D ( \cdot) $, et tel que $f \circ \Phi = \text{pr}_1$. On a alors :
Cette affirmation est une variation du lemme d’Ehresman que nous laissons en exercice au lecteur. Admettons la et montrons la formule de Picard-Lefschetz. Notons $c$ le point critique de $f$. Le lemme de Morse holomorphe (voir l’article Pinceaux et fibrations de Lefschetz et observer que la forme quadratique $x_1x_2$ sur $\mathbb C^2$ est équivalente à la forme $x_1^2 + x_2^2$) nous enseigne qu’il existe des coordonnées centrées en $c$ telles que $f (x_1 , x_2) = x_1 x_2$. L’application $\Psi = (x_1, x_2)$ exerce alors un biholomorphisme d’un voisinage $U'$ de $c$ vers un voisinage de l’origine dans $\mathbb C^2$. Quitte à multiplier $f$ et les coordonnées $x_i$ par des constantes strictement positives bien choisies, nous pouvons supposer que $ \Psi (U')$ contient un voisinage du bidisque fermé $\overline{\mathbb D} \times \overline{\mathbb D}$. Nous noterons $U = \Psi^{-1} (\overline{\mathbb D} \times \overline{\mathbb D})$.
Considérons alors la surface $F_0 ' = F_0 \setminus \big( (\mathbb D \times 0) \cup (0 \times \mathbb D) \big)$. Il s’agit d’une surface compacte avec deux composantes de bord $\partial ^\pm F_0'$ :
$$ \partial ^+ F_0' = \partial \mathbb D \times 0 \text{ et } \partial ^-F_0 ' = 0\times \partial \mathbb D. $$
Nous avons une déformation des bords de $F_0'$ dans les fibres voisines, définie sur un voisinage de $\partial F_0' \times \overline{\mathbb D}$ par
$$\Phi (z, ( x_1 ,0) ) = ( x_1 , \frac{z}{x_1} ) \text{ et } \Phi (z, (0, x_2) ) = ( \frac{z}{x_2} , x_2) .$$
Comme $F_0'$ ne contient aucun point singulier de la fibration, cette déformation se prolonge en une déformation du domaine $F_0'$, c’est à dire qu’il existe $\eta >0$ et une extension de $\Phi$ définie sur un voisinage de $F_0' \times \overline{\mathbb D_\eta}$.
Soit $\theta$ un nombre entre $0$ et $2\pi$. Nous allons construire explicitement une famille d’homéomorphismes $\Psi_\theta : F_\eta \rightarrow F_{\eta \exp (i\theta)} $ qui dépendent continûment de $\theta$. Le domaine de $F_{\eta \exp(i\theta)} $ extérieur à $\text{Int}(U)$ s’identifie à $F_0 '$ via
$$p\in F_0' \mapsto \Phi (\eta \exp(i\theta), p)\in F_{\eta \exp(i\theta)} \setminus \text{Int} (U) .$$
Sur ce domaine, on définit $\Psi_\theta$ par la relation
$$ \Psi_\theta ( \Phi (\eta, p ) ) = \Phi (\eta \exp (i\theta) , p) .$$
L’intersection de $F_{\eta \exp (i\theta)} $ avec $U$ est un anneau paramétré par l’anneau $A= \{ \eta \leq |x_1|\leq 1 \}$ via
$$ x_1 \in A \mapsto (x_1, \eta \exp (i\theta) /x_1) \in F_{\eta \exp(i\theta)} \cap U.$$
L’extension de $\Psi_\theta$ à l’intersection de $F_{\eta}$ avec $U$ est définie par une formule du type
$$ \Psi_\theta (x_1, \eta / x_1) = ( \psi_\theta (x_1) , \eta \exp (i\theta) \psi_\theta (x_1)^{-1} ) $$
où $\psi_\theta: A \rightarrow A$ est une famille de difféomorphismes de l’anneau qui vérifie
$$ \psi_\theta (x_1) = x_1 \text{ si } |x_1|=1 \text{ et } \psi_\theta (x_1) = \exp (i\theta ) x_1 \text{ si } |x_1|= \eta. $$
On peut par exemple choisir une famille de twists $\psi_\theta ( r \exp (i\alpha) ) = r \exp (i (\alpha + A_\theta(r)) )$ où $A_\theta$ est une fonction qui vaut $0$ en $1$ et $\theta$ en $\eta$, e.g. $A_\theta(r)= \frac{(1-r)\theta}{1-\eta}$. On constate donc que le difféomorphisme $\Psi_{2\pi}$ est un twist complet à droite dans l’anneau $F_\eta \cap U$, et l’identité à l’extérieur de ce dernier.
C.Q.F.D.
La classe d’isotopie de l’âme du support du twist de Dehn dans la formule de Picard-Lefschetz est appelée un cycle évanescent. Observez qu’une telle courbe est homotope à un point dans $X$, puisqu’elle est contenue dans un ouvert de $X$ difféomorphe à $\mathbb D \times \mathbb D $, alors qu’elle n’est a priori pas isotope à un point dans $F_{z_0}$. C’est ce qui explique la terminologie "évanescente". Pour une illustration encore plus convaincante, nous renvoyons à l’article Groupe fondamental des fibrations de Lefschetz.
Terminons en observant que notre démonstration de la formule de Picard-Lefschetz fournit une forme normale des voisinages des fibres singulières. Si la base est la sphère de Riemann $\mathbb P^1(\mathbb C)$, le lecteur pourra se convaincre que la représentation de monodromie caractérise complètement la fibration $f$ à conjugaison topologique près. Dans l’article Reconstruction topologique d’une fibration de Lefschetz, nous fournissons un modèle topologique pour l’espace total d’une fibration de Lefschetz, qui ne dépend que de sa représentation de monodromie. La construction est en fait plus générale, et permet de construire tout un tas de variétés de dimension quatre, dont les groupes fondamentaux et les groupes d’homologie se calculent exactement comme ceux des “vraies” fibrations de Lefschetz.
[1] Herbert Clemens. A Scrapbook of Complex Curve Theory. Springer, 1980. On pourra notamment consulter le chapitre sur l’équation de Picard-Fuchs.
[2] Sur les fonctions Fuchsiennes. Acta Mathematica. Tome 1 (1882), 193-294.
[3] Cette technique est donc beaucoup plus générale, et peut être adaptée telle quelle à des fibrations de Lefschetz dont les fibres sont de dimension supérieures.

