> Surfaces complexes > B-A-BA de topologie des variétés algébriques complexes

B-A-BA de topologie des variétés algébriques complexes

Le but de ce bloc est d’étudier les cycles induits par les sous-variétés algébriques des espaces projectifs complexes. On espère convaincre le lecteur que topologie et géométrie algébrique sont des sujets intimement reliés. Il est de toutes façons très clair qu’on a envie d’étudier les variétés algébriques du point de vue de l’Analysis Situs : contemplez par exemple la surface suivante.

Nous traiterons ici seulement le cas complexe, qui est paradoxalement plus simple. Commençons par illustrer ceci en démontrant par des méthodes topologiques le célèbre

Théorème de d’Alembert-Gauss

Un polynôme complexe en une variable de degré $d>0$ admet $d$ racines complexes, comptées avec multiplicité.

Démonstration. On note

$\mathbb P^1(\mathbb C) = \mathbb C \cup \{ \infty\}$ la sphère de Riemann : elle est construite en recollant deux copies de

$\mathbb C$ le long de

$\mathbb C^*$ via la transformation

$z\mapsto 1/z$ . Il s’agit d’une surface de Riemann compacte connexe, homéomorphe à la sphère. Un polynôme

$P \in \mathbb C [z]$ non constant induit une fonction holomorphe non constante

$f$ de

$\mathbb P^1 (\mathbb C)$ dans elle-même. En effet, dans la coordonnée

$z$ est est définie par

$f(z) = P(z)$ , et dans la coordonnée

$Z = 1/z$ , on a

$f (Z) = 1/P(1/Z)$ qui se prolonge bien en

$Z=0$ en une fonction holomorphe du type

$f(Z) = Z^d g(Z)$ , où

$g$ est une fonction analytique de

$Z$ qui ne s’annule pas au point à l’infini

$Z=0$ . Il s’agit donc d’un revêtement ramifié (voir le bloc Revêtements ramifiés entre surfaces). La sphère de Riemann étant connexe, chacun de ses points admet donc le même nombre de pré-images par

$f$ , comptées avec multiplicité. On conclut en remarquant que la pré-image du point à l’infini est le point à l’infini, et que sa multiplicité est égale à

$d$ .

C.Q.F.D.

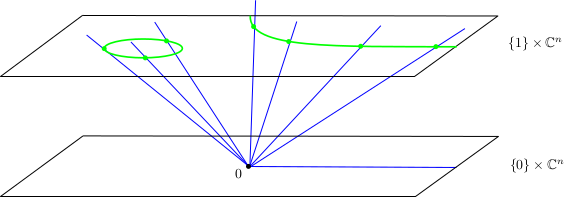
Comme dans la démonstration du théorème de d’Alembert-Gauss , il est naturel de compactifier un espace affine $\mathbb C^n$ , en lui adjoignant un ensemble de points « à l’infini, » qui correspondent aux directions possibles dans $\mathbb C^n$ , c’est-à-dire à l’ensemble des droites de $\mathbb C^n$ passant par un point donné, disons l’origine. L’espace obtenu est appelé l’espace projectif complexe. Une telle compactification est très utile en géométrie algébrique, les ensembles algébriques se compactifiant bien dans l’espace projectif. Par exemple, on sait bien que les courbes algébriques dans $\mathbb C^n$ ont des branches à l’infini, qui sont asymptotes à une certaine direction, il suffit de rajouter ces directions pour compactifier la courbe.

Formellement, on définit l’espace projectif complexe de dimension $n$ comme étant l’ensemble des droites de l’espace vectoriel $\mathbb C^{n+1}$ passant par l’origine : on le note $\mathbb P^n (\mathbb C)$ . On peut donc le voir comme le quotient de $\mathbb C^{n+1} \setminus 0$ par l’action de $\mathbb C^*$ par multiplication par un scalaire. Il hérite de cette façon d’une structure de variété complexe compacte, pour laquelle

$\mathbb C^ * \rightarrow \mathbb C^{n+1} \setminus 0 \rightarrow \mathbb P^n (\mathbb C)$

est une fibration holomorphe. Si $(x_0, \ldots, x_n)$ est un point de $\mathbb C^{n+1} \setminus 0$ , on note $[x_0 : \ldots : x_n]$ sa projection dans $\mathbb P^n (\mathbb C)$ ; ce sont les coordonnées homogènes.

$PNG$

Étant donné un hyperplan $H\simeq \mathbb C^n \subset \mathbb C^{n+1}$ , l’ensemble des droites qui ne sont pas contenues dans $H$ forment un ensemble qui s’identifie à $\mathbb C^n$ (naturellement à une transformation affine près de surcroît) : en effet, si l’on considère un espace affine $H'\simeq \mathbb C^n$ qui est parallèle à $H$ mais ne passe pas par l’origine, e.g. $H= \{0 \}\times \mathbb C^n$ et $H' = \{ 1\} \times \mathbb C^n$ , alors toute droite vectorielle de $\mathbb C^{n+1}$ non contenue dans $H$ intersecte $H'$ en un unique point. Les droites qui sont contenues dans $H$ forment un ensemble qui s’identifie naturellement à $\mathbb P^{n-1}(\mathbb C)$ . On obtient donc la décomposition

$\mathbb P^n (\mathbb C)= \mathbb C^n \cup \mathbb P^{n-1} (\mathbb C),$

formé d’un ouvert de carte affine $\mathbb C^n$ et d’un diviseur à l’ " infini" $\mathbb P^{n-1} (\mathbb C)$ correspondant bien à toutes les directions possibles de $\mathbb C^n$ .

Exercice

Utiliser cette décomposition pour montrer que le groupe fondamental de $\mathbb P ^n(\mathbb C)$ est trivial.

Proposition

L’homologie de $\mathbb P ^n (\mathbb C)$ est donnée par

$H_i (\mathbb P ^n (\mathbb C) , \mathbb Z ) \simeq \mathbb Z \text{ si } i \text{ est pair et } H_i (\mathbb P ^n (\mathbb C) , \mathbb Z) = 0 \text{ si } i \text{ est impair }.$

Plus précisément, $H_ {2k} (\mathbb P ^n (\mathbb C) , \mathbb Z ) = \mathbb Z [\mathbb P (W) ]$ , où $W\subset \mathbb C^{n+1}$ est un sous-espace linéaire de dimension $k+1$ .

Ce résultat est démontré dans le bloc Homologie des espaces projectifs, nous en redonnons une démonstration par soucis de complétude.

Démonstration. Prenons un hyperplan

$H \subset \mathbb C^{n+1}$ , et considérons un point

$p\in \mathbb P ^n(\mathbb C)$ extérieur à

$\mathbb P (H)$ . On pose

$U = \mathbb P^n (\mathbb C) \setminus \mathbb P (H) \text{ et } V = \mathbb P^n (\mathbb C)\setminus p.$

Observons que $U$ est une carte affine isomorphe à $\mathbb C^n$ , que $V$ se rétracte par déformation sur $\mathbb P (H)$ , et que $U\cap V$ se rétracte par déformation sur la sphère $\mathbb S^{ 2n-1}$ . La suite de Mayer-Vietoris

$H_i (U\cap V ,\mathbb Z) \rightarrow H_i (U,\mathbb Z) \oplus H_i (V,\mathbb Z) \rightarrow H_i (\mathbb P^n (\mathbb C), \mathbb Z) \rightarrow H_{i-1} (U\cap V,\mathbb Z)$

et le fait que l’homologie de $\mathbb S^{2n+1}$ est

$H_i (\mathbb S^{2n+1},\mathbb Z) = 0 \text{ si }i \neq 0, 2n+1 \text{ et } H_i (\mathbb S^{2n+1},\mathbb Z) \simeq \mathbb Z \text{ sinon.}$

donnent le résultat.

C.Q.F.D.

Définition

Étant donnée une certaine famille de polynômes homogènes sur $\mathbb C^{n+1}$ , l’ensemble des droites de $\mathbb C^{n+1}$ sur lesquelles tous ces polynômes s’annulent simultanément est appelée une sous-variété algébrique de $\mathbb P^n (\mathbb C)$ .

Ces variétés sont en particulier des sous-variétés analytiques complexes de $\mathbb P^n(\mathbb C)$ . Un théorème de Chow établit que ce n’est pas une situation plus générale : les sous-variétés analytiques complexes de $\mathbb P^n (\mathbb C)$ sont nécessairement algébriques. Il sera néanmoins avantageux d’énoncer les résultats dans le cadre des sous-variétés complexes, même si a posteriori on sait que ce sont les mêmes objets.

Une sous-variété complexe lisse $X\subset \mathbb P^n (\mathbb C)$ (a fortiori une sous-variété algébrique lisse) étant munie de l’orientation venant de sa structure complexe, elle définit un cycle $[X] \in H_ { 2k} (\mathbb P^n (\mathbb C), \mathbb Z)$ , où $k$ est la dimension complexe de $X$ : il s’agit de sa classe fondamentale, voir Orientation et classe fondamentale. Le calcul de l’homologie de $\mathbb P^n(\mathbb C)$ montre que cette classe est un multiple du cycle induit par un sous-espace projectif de dimension $k$ : il existe un entier $d$ tel que $[X] = d \cdot [\mathbb P (W)]$ , où $W$ est un sous-espace linéaire de $\mathbb C^{n+1}$ de dimension $k+1$ . Cet entier est unique et s’appelle le degré de $X$ .

En fait, on peut toujours définir la classe fondamentale de $X$ , même dans le cas où elle est singulière. Cela nous amènerait trop loin de le faire dans ce bloc, nous nous contentons juste de commenter le cas des courbes algébriques planes. Dans ce cas, on sait qu’il n’existe qu’un nombre fini de singularités, et qu’au voisinage de toute singularité, la courbe algébrique peut être paramétrée holomorphiquement par un bouquet de disques attachés en un point (paramétrisation de Newton-Puiseux). Ainsi, une courbe algébrique plane, même singulière, peut être paramétrée par le quotient d’une surface de Riemann compacte par une relation dont toutes les classes sont des points, sauf un nombre fini qui sont finies, comme sur la figure ci-dessous. Un tel objet admet donc une classe fondamentale : l’image de la classe fondamentale de la surface de Riemann.

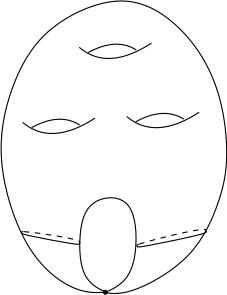
$PNG - 16.2 ko$
Courbe algébrique complexe singulière

Le résultat de positivité suivant est absolument fondamental en géométrie algébrique complexe. Pour l’énoncer, rappelons que si $N_1$ et $N_2$ sont deux sous-variétés de dimensions complémentaires d’une variété $N_3$ , toutes orientées, et si $N_1$ et $N_2$ s’intersectent transversalement en un point $p$ , alors l’indice d’intersection de $N_1$ et $N_2$ en $p$ est $1$ ou $-1$ , suivant que les orientations induites par $N_1, N_2$ et $N_3$ sur $T_p N_3= T_p N_1 \oplus T_p N_2$ sont les mêmes, ou non.

Proposition

L’indice de deux sous-variétés complexes s’intersectant transversalement en un point est égal à $1$ .

Démonstration. Il suffit de le faire pour des sous-espaces linéaires complexes transverses, et c’est évident dans ce cas.

C.Q.F.D.

Corollaire

Le degré d’une sous-variété complexe lisse de $\mathbb P^n (\mathbb C)$ de dimension $k$ est égal au nombre de ses points d’intersection avec un sous-espace projectif transverse de dimension $n-k$ . En particulier, le cycle induit par une sous-variété complexe lisse est non nul.

Démonstration. La première assertion découle du lemme précédent et de la formule qui dit que le produit d’intersection en homologie des classes fondamentales de deux sous-variétés transverses est égale à la somme des indices aux points d’intersection). Pour montrer la deuxième assertion, il suffit de montrer qu’étant donnée une sous-variété complexe lisse

$X$ de

$\mathbb P^n(\mathbb C)$ de dimension

$k$ , il existe un sous espace projectif transverse à

$X$ de dimension

$n-k$ . Or, introduisons la grassmannienne

$\text{Gr} (p,q)$ formée par l’ensemble des sous-espaces de dimension

$p$ dans un espace de dimension

$q$ , qui admet la structure d’une variété de dimension

$p (q-p)$ , comme le lecteur pourra le vérifier. Etant donné

$x\in X$ et une droite

$D$ dans l’espace tangent

$T_x X$ , l’ensemble des sous-espaces projectifs de dimension

$k$ tangent à

$X$ en

$x$ dans la direction

$D$ s’identifie à la grassmannienne

$\text{Gr}(n-k-1, n-1)$ . Du coup, l’ensemble des sous-espaces projectifs de dimension

$n-k$ qui admettent une tangence avec

$X$ peut être paramétré par un fibré en grassmanniennes

$\text{Gr}(n-k -1, n-1)$ au dessus de la projectivisation

$\mathbb P (TX)$ du fibré tangent à

$X$ : il s’agit d’une variété de dimension

$2k-1 + (n-k-1) k= (n-k+1)k -1$ . La dimension de l’espace de tous les sous-espaces projectifs de dimension

$n-k$ de

$\mathbb P^n (\mathbb C)$ est

$(n-k+1)k$ , qui est strictement supérieure. Un sous-espace générique de dimension

$n-k$ sera donc transverse à

$X$ .

C.Q.F.D.

Corollaire

Soient $P$ un polynôme homogène de degré $d$ sur $\mathbb C^{n+1}$ . L’hypersurface $P=0$ , si elle est lisse, a pour degré $d$ .

Démonstration. Cela résulte du corollaire précédent et du théorème de d’Alembert-Gauss.

C.Q.F.D.

Proposition

Soient $X$ et $Y$ deux sous-variétés complexes de $\mathbb P^n (\mathbb C)$ qui sont transverses, i.e. $T_p X + T_p Y= T_p \mathbb P^n (\mathbb C)$ en tout $p\in X\cap Y$ . Alors

$d (X\cap Y) = d(X) \cdot d(Y).$

Démonstration. Soient

$k$ et

$l$ les dimensions respectives de

$X$ et

$Y$ et

$m = k+l -n$ la dimension de

$X \cap Y$ . On a

$[X]= d(X) \cdot [\mathbb P^k]$ et

$Y = d(Y) \cdot [\mathbb P^l]$ . Du coup, puisque pour la même raison de positivité,

$[X\cap Y] = [X ] \cdot [Y]$ , on en déduit

$[X\cap Y ] = d(X) \cdot d(Y) [\mathbb P^k] \cap [\mathbb P^l ] = d(X) \cdot d(Y) \cdot [\mathbb P^m].$

C.Q.F.D.

Corollaire (théorème de Bézout)

Deux sous-variétés complexes lisses $X$ et $Y$ transverses et de dimensions complémentaires s’intersectent en $d(X) d(Y)$ points.

Démonstration. Cela repose sur la proposition précédente ainsi que sur le fait que

$\mathbb P^0 (\mathbb C)$ est un point.

C.Q.F.D.

Corollaire

Une sous-variété complexe lisse de $\mathbb P^n (\mathbb C)$ de dimension complexe $k \geq n/2$ est connexe.

Démonstration. Soit

$X$ une telle variété, et supposons par contradiction qu’elle admette deux composantes connexes

$X'$ et

$X''$ distinctes. Ces dernières définissent des cycles

$[X']$ et

$[X'']$ de

$H_{2k} (\mathbb P^n (\mathbb C), \mathbb Z)$ qui sont tous les deux des multiples non nuls de

$[\mathbb P^k(\mathbb C)]$ . On doit donc avoir

$[X'] \cdot [X''] \neq 0$ , ce qui contredit le fait que

$X'$ et

$X''$ sont disjoints. C.Q.F.D.

Nous concluons ce bloc par le calcul de la topologie des courbes algébriques lisses du plan projectif complexe. Nous savons qu’elles sont connexes, il nous suffit donc de calculer leur genre. Voir Classification des surfaces par la théorie de Morse.

Théorème

Le genre d’une courbe algébrique lisse du plan projectif complexe de degré $d$ est donné par $g = (d-1) (d-2) /2$ .

Démonstration. Les courbes algébriques de degré

$1$ sont les droites projectives complexes, qui sont de genre nul. La formule est bien satisfaite dans ce cas. Soit alors

$C$ une courbe algébrique lisse de degré

$d >1$ . La courbe

$C$ n’a qu’un nombre fini de droites d’inflexion. Prenons un point

$p \in \mathbb P^2(\mathbb C)$ qui n’appartient pas à l’union de ces droites, une droite

$D$ qui ne contient pas

$p$ , et considérons la projection

$\pi : C \rightarrow D$ de centre

$p$ . Il s’agit d’un revêtement ramifié de degré

$d$ . La formule de Riemann-Hurwitz (voir Revêtements ramifiés entre surfaces) montre que la caractéristique d’Euler de

$C$ est donnée par

$\chi (C) = d \chi (D) - r = 2d -r$

où $r$ est le nombre de points de ramification de $\pi$ , comptés avec multiplicité. Puisque le point $p$ est choisi en dehors des droites d’inflexion de la courbe $C$ , tous ces points de ramification sont simples.

Prenons des coordonnées homogènes $[x:y:z]$ de $\mathbb P ^2$ de sorte que le point $p$ soit le point $[1: 0: 0]$ , la droite $D$ soit définie par $x = 0$ . La projection $\pi$ est définie dans ces coordonnées par $\pi ([ x:y:z]) = [0:y:z]$ .
Si $P= 0$ est une équation homogène de $C$ de degré $d$ , les points de ramification de $\pi$ sont alors donnés par les équations

$P = 0 \text{ et } \frac{\partial P}{\partial x} = 0 .$

Comme ces points ne sont pas des points d’inflexion de $C$ , la courbe définie par $\frac{\partial P}{\partial x} = 0$ est transverse à $C$ et de degré $d-1$ . Le théorème de Bezout montre donc que $\pi$ a exactement $r = d (d-1)$ points de ramification.

On en déduit $\chi (C) = d(3- d)$ , et donc le résultat car $\chi (C) = 2g-2$ .

C.Q.F.D.

[1] Les français ont pris l’habitude d’associer la nom de d’Alembert à ce théorème, ce qui n’a pourtant pas grand sens. Même en donnant un sens très flou au mot « démonstration », attribuer cela à d’Alembert n’est qu’un signe de chauvinisme.

B-A-BA de topologie des variétés algébriques complexes

Rubrique(s) mère(s)

Dans la même rubrique :