
|
> Homologie > Interprétation géométrique du produit d’intersection Interprétation géométrique du produit d’intersection |
Soit $V$ une variété lisse compacte, orientable et sans bord, de dimension $d$. On rappelle qu’il existe un isomorphisme (de dualité de Poincaré)
$$D:H_i (V) \stackrel{\sim}{\to} H^{d-i} (V)$$
tel que pour tout $a \in H_i (V)$ on ait $D(a) \cap [V] = a$. [1]
On définit le produit d’intersection
$$H_i (V) \times H_j (V) \stackrel{\cdot}{\to} H_{i+j-d} (V)$$
par la formule
$$a \cdot b = D^{-1} (D(b) \cup D(a) )= (D(b) \cup D(a)) \cap [V]$$
Ce qu’on peut écrire $a\cdot b = D(b) \cap (D(a) \cap [V]) = D(b) \cap a$ ou encore $D(a \cdot b) = D(b) \cup D(a)$.
Il n’est pas difficile de vérifier que le produit d’intersection est associatif et « presque commutatif » :
On a :
$$a \cdot (b \cdot c) = (a\cdot b ) \cdot c$$
et
$$a \cdot b = (-1)^{(d -\mathrm{deg}(a))(d-\mathrm{deg}(b))} b \cdot a.$$
On a :
$$D(a\cdot (b \cdot c)) = D(b\cdot c) \cup D(a) = D(c) \cup D(b) \cup D(a).$$
De sorte que la première assertion découle de l’associativité du produit cup. La seconde découle de sa commutativité au sens gradué.
C.Q.F.D.
$$ $$
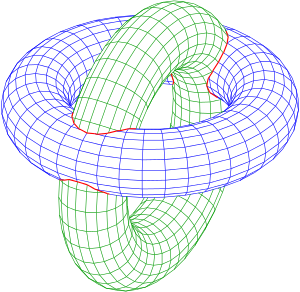
Soient $W_1$ et $W_2$ deux sous-variétés orientées de $V$ et qui s’intersectent transversalement dans $V$. On a alors :
$$[W_1 ] \cdot [W_2] = [W_2 \cap W_1].$$
Sur la figure, l’intersection de la classe des tores bleu et vert est la classe de la courbe rouge.
1. On a noté abusivement $[W_1]$, $[W_2]$ et $[W_2 \cap W_1]$ les images des classes fondamentales de $W_1$, $W_2$ et $W_2 \cap W_1$ dans $H_\bullet (V)$ par les morphismes induits par les inclusions dans $V$. En cas de possible confusion on notera plutôt $[W_1]_V$, $[W_2]_V$ et $[W_2 \cap W_1]_V$ ces classes.
2. Pour que la classe $[W_2 \cap W_1]$ ait un sens il faut toutefois spécifier une orientation de $W_2 \cap W_1$. On suit la convention suivante : étant donné un point $x \in W_2 \cap W_1$, un repère en $x$ de $W_2 \cap W_1$ peut être complété en un repère de $W_1$ de manière cohérente avec l’orientation de $W_1$ puis on complète de même par des vecteurs tangents à $W_2$ pour obtenir un repère de $V$. Si le repère obtenu est cohérent avec l’orientation de $V$ alors notre repère de $W_2 \cap W_1$ est considéré comme positif sinon il est négatif. On notera qu’une fois cette convention adoptée, la notation $[W_2 \cap W_1]$ tient compte de l’ordre entre $W_1$ et $W_2$.
$$ $$
Classe de Thom
Soient $W$ une variété compacte orientée de dimension $n$ et $\pi : N \to W$ un fibré (topologique) orientable en disques de dimension $k$ au-dessus de $W$. On suppose fixé un choix d’orientation de $N$ [2]. On note $i : W \hookrightarrow N$ la section nulle. Il lui correspond un morphisme de restriction
$$i^* : H^{\bullet} (N) \stackrel{\sim}{\to} H^\bullet (W)$$
inverse de
$$\pi^* : H^\bullet (W) \to H^\bullet (N).$$
La classe de Thom de la fibration $\pi$ est la classe $\tau \in H^k (N , \partial N)$ telle que [3]
$$\tau \cap [N] = i_* ([W]).$$
Soient $W$ et $V$ deux variétés compactes, connexes et orientables de dimension respectives $n$ et $m$. Une application continue $f:W \to V$ induit des morphismes $f_*$ en homologie et $f^*$ en cohomologie. Si l’on suppose de plus que $f(\partial W) \subset \partial V$, on peut lire ces morphismes à travers la dualité de Poincaré.
On note
$$f^{!} : H^{n-p} (W, \partial W) \to H^{m-p} (V, \partial V)$$
l’application $f^{!} = D_V f_* D_W^{-1}$ et
$$f_{!} : H_{m-p} (V, \partial V) \to H_{n-p} (W, \partial W)$$
l’application $f_{!} = D_W^{-1} f^* D_V$.
Le théorème suivant explicite les morphismes $i^!$ et $i_!$ associée à la section nulle $i$ d’un fibré en disques.
Soient $W$ une variété compacte orientée de dimension $n$ et $\pi : N \to W$ un fibré (topologique) orienté en disques de dimension $k$ au-dessus de $W$. Soit $\tau$ la classe de Thom de ce fibré. Alors le morphisme
$$i^{!} : H^p (W) \to H^{p+k} (N , \partial N)$$
est un isomorphisme égal au composé de l’isomorphisme $\pi^* : H^p (W) \to H^p (N)$ par le morphisme $H^p (N) \stackrel{ \cdot \cup \tau}{\longrightarrow} H^{p+k} (N , \partial N)$ « cup produit avec la classe de Thom ».
De même
$$i_! = \pm \pi_* (\tau \cap \cdot) : H_{p+k} (N, \partial N) \to H_p (W)$$
est un isomorphisme.
Démonstration. On ne démontre que la première partie du théorème, la deuxième partie se démontrerait de la même manière. Le morphisme $i^!$ est un isomorphisme car $i_*$ en est un. Il nous reste à démontrer que $i^! = \pi^* (\cdot ) \cup \tau$.
Considérons pour cela deux classes $\alpha$ et $\beta$ telles que
$$\beta = i^* (\alpha ) \Longrightarrow \alpha = \pi^* (\beta).$$
Il découle des définitions que
$$i^! (\beta) = D_N i_* D_W^{-1} (\beta) = D_N i_* (i^* (\alpha ) \cap [W] ).$$
Par fonctorialité du produit cap le membre de droite est égal à $D_N (\alpha \cap i_* ([W]))$ qui, par définition de la classe de Thom, est égal à $D_N (\alpha \cap (\tau \cap [N]))$. Il découle finalement des définitions que
$$i^! (\beta) = D_N ((\alpha \cup \tau ) \cap [N]) = \alpha \cup \tau = \pi^* (\beta ) \cup \tau.$$
C.Q.F.D.
Interprétation géométrique du produit d’intersection
Soit $i: W \hookrightarrow V$ un plongement lisse de variétés lisses, connexes, compactes et orientées. Soit $k$ la codimension de $W$ dans $V$. On admettra que le fibré normal à $W$ dans $V$ est un fibré $N$ en disques (de dimension $k$) et qu’il existe un plongement $N \hookrightarrow V$, un « voisinage tubulaire » de $W$.
Maintenant les applications
$$C^\bullet (N , N \setminus W) \to C^\bullet (V) \quad \mbox{«extension par 0»}$$
et
$$C_\bullet (N) \hookrightarrow C_\bullet (V) \quad \mbox{«inclusion»}$$
font commuter le diagramme
$$ \begin{CD} C^k (N, N \setminus W) \times C_{\ell} (N) @>\cap>> C_{\ell -k} (N) \\ @VVV @VVV \\ C_k (V) \times C_\ell (V) @>\cap>> C_{\ell -k} (V). \end{CD} $$
En particulier, via l’isomorphisme d’excision $H^k (N , \partial N) \to H^k (N , N \setminus W)$ suivi du morphisme $H^k (N , N \setminus W) \to H^k (V)$ (associé à l’application d’extension par 0), la classe duale $D_N ([W]_N )$ s’envoie sur $D_V ([W]_V )$. La proposition/définition qui suit découle alors du théorème d’isomorphisme de Thom (pour $p=0$).
La classe
$$\tau_W^V := D_V ([W]_V) \in H^k (V)$$
est l’image de la classe de Thom du fibré $N \to W$ par
$$H^k (N , \partial N) \stackrel{\sim}{\to} H^k (N , N \setminus W) \to H^k (V).$$
On l’appelle classe de Thom de $W$ dans $V$.
Noter que la classe de Thom vérifie
$$\tau_W^V \cap [V] = [W] .$$
$$ $$
Démonstration du théorème d’interprétation géométrique du produit d’intersection. Supposons maintenant données $W_1$, $W_2 \subset V$ comme dans le théorème. On a alors :
$$[W_1] \cdot [W_2] = (\tau_{W_1}^V \cap [V]) \cdot (\tau_{W_2}^V \cap [V]) = (\tau_{W_2}^V \cup \tau_{W_1}^V ) \cap [V].$$
Il reste à interpréter le produit cup $\tau_{W_2}^V \cup \tau_{W_1}^V$. Pour cela supposons que $W_1$ et $W_2$ se rencontrent transversalement. Alors les voisinages tubulaires sont compatibles et on a
$$\tag{1} \tau_{W_2 \cap W_1}^V = (i_{W_1}^V)^* (\tau_{W_2}^V )$$
et
$$[W_2 \cap W_1]_V = (i_{W_2 \cap W_1}^V )_* ([W_2 \cap W_1 ]).$$
Mais il découle des définitions que
$$ (i_{W_2 \cap W_1}^V )_* ([W_2 \cap W_1 ]) = (i_{W_1}^V)_* (i_{W_2 \cap W_1}^{W_1} )_* ([W_2 \cap W_1 ])$$
$$ = (i_{W_1}^V)_* (\tau_{W_2 \cap W_1}^{W_1} \cap [W_1 ]).$$
Puis (1) implique que
$$ (i_{W_1}^V)_* (\tau_{W_2 \cap W_1}^{W_1} \cap [W_1 ]) = (i_{W_1}^V)_* ((i_{W_1}^V)^* (\tau_{W_2 }^V ) \cap [W_1 ]).$$
On déduit donc de la fonctorialité du produit cap que
$$[W_2 \cap W_1]_V = \tau_{W_2 }^V \cap (i_{W_1}^V)_* ([W_1]) = \tau_{W_2}^V \cap (\tau_{W_1}^V \cap [V])$$
$$= ( \tau_{W_2}^V \cup \tau_{W_1}^V) \cap [V] = [W_1] \cdot [W_2].$$
C.Q.F.D.
[1] Ici
$$H^{d-i} (V) \times H_i (V) \stackrel{\cap}{\to} H_i (V)$$
est le produit cap d’« intégration partielle » et $[V]$ désigne la classe fondamentale de $V$ (associée à un choix d’orientation de $V$). Remarquons que c’est plus souvent l’inverse $D^{-1}$ de $D$, donnée par $x \mapsto x \cap [V]$, que l’on appelle isomorphisme de dualité de Poincaré.
[2] Le fibré $N$ est donc donné par des changements de trivialisations $\theta_x : \mathbb{D}^k \to \mathbb{D}^k$ linéaires et préservant l’orientation.
[3] La classe $\tau$ ainsi définie existe bien en vertu de la dualité de Poincaré pour les variétés à bord selon laquelle on a un isomorphisme de dualité
$$D_N : H_n (N) \stackrel{\sim}{\to} H^{k} (N , \partial N)$$
dont l’inverse est le produit cap avec la classe fondamentale $[N]$.

