Contexte historique

Afin de pleinement apprécier la créativité de Poincaré en Analysis Situs, il est nécessaire de la replacer dans son contexte historique.

On peut penser à son environnement familial ou social. Nous n’en parlerons pas ici, en renvoyant les lecteurs intéressés vers les Archives Henri Poincaré, vers le livre consacré à son ami par Paul Appell ou vers la « Biographie au quotidien » de Jean-Marc Ginoux et Christian Gerini. Qu’il nous suffise de présenter trois photos [1] :

Nous nous intéresserons plutôt au contexte mathématique de l’époque. Le Maître lui-même mentionne dans l’Introduction à l’article fondateur « Analysis Situs » certains des travaux qui l’ont influencé, qu’il s’agisse de ceux d’autres mathématiciens ou des siens propres. Nos Commentaires de cette Introduction apportent quelques précisions à ce sujet.

Nous avons choisi de vous présenter aussi la manière dont Poincaré expliquait l’importance de la recherche en Analysis Situs à un public plus large :

• Comment Poincaré présentait l’Analysis Situs au « grand public »

Les principales notions introduites dans l’« Analysis Situs », puis développées dans ses « Compléments », sont celle de groupe fondamental, la relation d’homologie entre cycles ainsi que les nombres de Betti qu’elle permet de définir. Les objets que Poincaré étudie plus particulièrement grâce à ces notions sont les surfaces algébriques complexes ainsi que les variétés de dimension $3$. Dans le « Cinquième Complément », qui marque la fin de la série d’articles à laquelle est consacré ce site, Poincaré utilise une nouvelle technique de décomposition de ces dernières, dans laquelle on peut voir un prototype de théorie de Morse.

Pour ces raisons, nous avons choisi d’examiner certains textes dans lesquels on peut reconnaître grâce à notre recul historique des précurseurs de l’homologie, du groupe fondamental et de la théorie de Morse, ainsi que de l’étude des variétés de petite dimension faite grâce à ces outils.

L’une des grandes obsessions de Poincaré a été l’étude des équations différentielles. C’est le projet de les résoudre toutes qui le mena à conjecturer, puis à proposer des preuves de plus en plus raffinées du théorème d’uniformisation des surfaces de Riemann. Henri Paul de Saint Gervais a consacré son premier travail à cette aventure. On peut y apprendre entre autres que, lors de son attaque d’une classe particulière d’équations différentielles, qu’il appella Fuchsiennes, Poincaré découvrit qu’il pouvait en construire des solutions grâce à la géométrie non-Euclidienne de Bolyai et Lobachevski. Et cela en construisant d’abord des pavages polygonaux du plan de la géométrie non-Euclidienne.

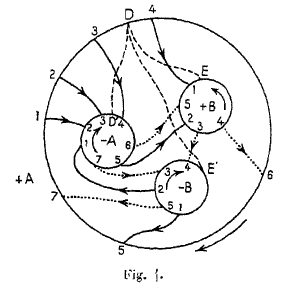
Les réflexions de Poincaré au sujet de ces pavages, et de leurs liens avec les surfaces de Riemann compactes qu’ils permettent d’uniformiser, le menèrent à la notion générale de groupe fondamental d’une variété de dimension quelconque. C’est ce processus de pensée qui est raconté dans notre article :

• La genèse du groupe fondamental chez Poincaré

Quant à l’idée d’homologie, elle prend sa source principale dans les travaux de Riemann des années 1850, consacrés à l’Analysis Situs des surfaces qui portent son nom. Bien sûr, elle n’avait pas surgi de nulle part, mais de la réflexion de Riemann au sujet de la théorie des intégrales Abeliennes. L’un des membres d’Henri Paul de Saint Gervais a replacé cela dans un large paysage historique dans un livre consacré à la notion mathématique de genre.

Mais Riemann a aussi essayé d’étudier la structure topologique des variétés de dimension quelconque. Témoignent de cela quelques notes manuscrites retrouvées après sa mort, et publiées de manière posthume. Riemann y décrivait une approche de l’étude topologique des variétés de dimension arbitraire en imitant celle qu’il avait pratiquée dans le cas des surfaces : par découpages et déformations successifs. L’esprit de ces notes est très proche de celui d’un article publié par Betti en 1871, après la mort de Riemann. En fait, Betti et Riemann avaient discuté longuement de l’Analysis Situs des variétés de dimension quelconque. Deux lettres de Betti à son ami Tardy reflètent ces discussions. Nous étudions le contenu des notes de Riemann et des lettres de Betti à Tardy dans nos articles :

• Les idées de Riemann sur l’Analysis Situs en dimension quelconque
• Les discussions entre Riemann et Betti sur l’Analysis Situs

Pour avoir une vue d’ensemble de la théorie homologique générale développée par Poincaré dans l’« Analysis Situs » puis dans son Premier et son Deuxième « Complément », on pourra lire notre article :

• Approches de l’homologie chez Poincaré

Dans le Troisième et le Quatrième « Complément », Poincaré applique la théorie du groupe fondamental et de l’homologie développée jusque là à l’étude de certaines surfaces algébriques complexes. Topologiquement, il s’agit de variétés de dimension $4$. En fait, Poincaré s’était déjà confronté à des aspects homologiques des variétés de dimension $4$ dans un article de 1886. Cet article était consacré à l’extension de la théorie des résidus du cas des intégrales simples à une variable complexe considéré par Cauchy à celui des intégrales doubles à deux variables. Dans l’article suivant, nous examinons les aspects homologiques de ce travail de Poincaré sur les résidus :

• Poincaré et les résidus des intégrales doubles

Au milieu du XIX-ème siècle, ce n’est pas seulement Riemann qui s’intéressait de près aux surfaces d’un point de vue topologique. À la même époque, Listing — qui est d’ailleurs le créateur du terme « topologie », qui allait remplacer celui d’« Analysis Situs » au XXème siècle — avait l’ambitieux programme de décrire toutes les surfaces de l’espace usuel. En termes modernes, il s’agissait de classifier à isotopie près les espaces topologiques sous-jacents aux complexes cellulaires de dimension $2$ de $\mathbb{R}^3$. Ce problème est encore ouvert à l’heure actuelle. Dans l’article suivant, nous examinons les diagrammes introduits par Listing à cette occasion, et leur relation avec ceux introduits une quarantaine d’années plus tard par Heegaard :

• Des diagrammes de Listing à ceux de Heegaard

Les « diagrammes » de Heegaard sont encore amplement utilisés de nos jours, même si ce terme ne désigne plus exactement ce que Heegaard appelait ainsi. Et c’est à l’aide d’un diagramme de Heegaard au sens moderne que Poincaré allait introduire sa célèbre sphère d’homologie non simplement-connexe dans son « Cinquième complément » :

Poincaré explique comment on peut parvenir à un tel diagramme en partant d’une fonction de Morse sur une variété close de dimension $3$. Ce qu’on appelle de nos jours « théorie de Morse » n’allait s’épanouir qu’à partir des années 1920. Mais des prototypes de cette théorie étaient apparus dès la fin des années 1850. Le plus ancien prototype que nous connaissons est un article de Cayley de 1859. Les deux articles suivants sont consacrés d’une part à l’examen du contenu de cet article de Cayley, et d’autre part à la description du développement de la théorie de Morse à partir de ce travail précurseur et jusqu’aux travaux de Smale, un siècle plus tard :

• L’article de Cayley sur les lignes de niveau et de plus grande pente
• La théorie de Morse, de la topographie à la conjecture de Poincaré en grande dimension

Les lecteurs curieux d’explorer d’autres aspects du développement historique de la topologie algébrique, combinatoire, géométrique ou générale pourront se référer à notre liste bibliographique :

• Textes d’histoire des mathématiques