Poincaré et les résidus des intégrales doubles

Dans l’introduction de l’article « Analysis Situs » de 1895, l’un des arguments de Poincaré pour expliquer la nécessité de développer une intuition des « figures géométriques » vivant dans des espaces de dimension plus grande que trois est le suivant :

On sait quelle est l’utilité des figures géométriques dans la théorie des fonctions imaginaires et des intégrales prises entre des limites imaginaires, et combien on regrette leur concours quand on veut étudier, par exemple, les fonctions de deux variables complexes.

On peut y voir une allusion à l’article « Sur les résidus des intégrales doubles », que Poincaré avait publié en 1887, et dont il avait annoncé les principaux résultats dans une note parue l’année précédente.

Le but de ce chapitre est de présenter la partie centrale de cet article de 1887, qui constitue par bien des aspects un prélude de la définition des homologies dans l’article de 1895.

« Une question de langage »

Le but de l’article de Poincaré est d’étendre la théorie de Cauchy de l’intégration le long des chemins contenus dans le plan complexe. En effet, voici comment débute son article :

C’est à Cauchy que revient la gloire d’avoir fondé la théorie des intégrales prises entre des limites imaginaires ; cette théorie a pour ainsi dire doublé la puissance de l’Analyse mathématique [...]

Il semblait qu’il n’y avait plus qu’un pas à faire pour étendre cette théorie aux intégrales doubles et qu’on pouvait se promettre de cette extension d’aussi belles conquêtes que de la considération des intégrales simples. Il y avait là de quoi tenter l’ambition des géomètres et cependant, au bout de quarante ans, nous sommes à peine plus avancés qu’au premier jour.

Le reste de son introduction est consacré à la description de quelques essais infructueux d’autres mathématiciens, d’extension de la théorie de Cauchy au cas des intégrales de deux variables complexes.

Puis, au début de la section I de son article, il affirme que les difficultés qui ont empêché cette extension ne sont en somme qu’« une question de langage » :

Les difficultés auxquelles les géomètres se sont heurtés si souvent dans la théorie qui nous occupe n’ont rien d’essentiel et ne sont pour ainsi dire qu’une question de langage.

Dans l’étude des intégrales simples, on emploie un mode de représentation géométrique très commode et dont il semble qu’on pourrait difficilement se passer. On ne peut le transporter sans changement dans la théorie des intégrales doubles, pour une raison qu’il est aisé d’apercevoir.

Soient $\xi$ et $\eta$ deux variables complexes ; si nous posons

$$ \xi = x + i y , \eta = z + it$$

en séparant les parties réelle et imaginaire, nous aurons quatre variables $x,y,z$ et $t$. Nous ne pouvons les regarder comme les coordonnées d’un point dans l’espace, à moins de nous résigner à admettre un espace à quatre dimensions.

On se trouve donc en présence du dilemme suivant : il faut, ou renoncer à toute représentation ou employer l’hypergéométrie ; mais, dans ce dernier cas, on est exposé à rebuter la plupart des lecteurs, et de plus on ne possède que l’avantage d’un langage commode, mais incapable de parler aux sens.

Comme cette langue hypergéométrique répugne encore à beaucoup de bons esprits, je n’en ferai qu’un usage peu fréquent ; je crois néanmoins nécessaire de préciser ici le sens des termes que je lui emprunterai.

Ces termes sont ceux de « point », « hypersurface », « surface » et « ligne ». Chacun de ces objets est une « multiplicité » à un certain nombre de dimensions, c’est ce qu’il appellera une « sous-variété » de $\mathbb{R}^4_{x,y,z,t}$ dans l’« Analysis Situs ». Par exemple, il définit ici une hypersurface comme un « ensemble des points qui satisfont à une seule relation entre $x, y, z$ et $t$ ». Il pense très probablement à la condition supplémentaire que cette relation puisse s’écrire $f(x,y,z,t) =0$, avec en chacun des points de ce lieu d’annulation $f$ lisse et de différentielle non-nulle, mais il ne l’écrit pas [1].

Les surfaces d’intégration

Le vocabulaire précédent lui permet d’énoncer :

Une intégrale double doit être étendue à tous les points d’une surface. Nous aurons donc une surface d’intégration de même qu’on a, dans la théorie des intégrales simples, un chemin d’intégration.

[...] la surface d’intégration étant purement arbitraire ne sera pas forcément algébrique ; elle pourra être transcendante ou se composer de portions appartenant à diverses surfaces algébriques.

Il poursuit :

Je vais maintenant exposer les artifices à l’aide desquels je compte m’affranchir de la nécessité de considérations hypergéométriques.

Ces « artifices » consistent à définir d’abord une surface $S$ dans l’« espace ordinaire » de trois variables réelles $(\lambda, \mu, \nu)$, puis de prendre son image par une application rationnelle :

$$ \mathbb{R}^3_{\lambda, \mu, \nu} \longrightarrow \mathbb{R}^4_{x,y,z,t}.$$

Il suppose que cette application, une fois restreinte à $S$, ne devient pas un revêtement sur son image $S'$ :

Le genre de la surface $S$ (au point de vue de la géométrie de situation) sera aussi le même que le genre de la surface $S'$, à moins que le point $x,y,z,t$ ne décrive deux ou plusieurs fois la surface $S'$, ce que nous ne supposerons pas.

Il suppose aussi que l’image de l’« espace ordinaire » par l’application rationnelle précédente est une « hypersurface ». C’est elle qui permet d’être « affranchi de l’hypergéométrie » :

Tant donc que le point $x,y,z,t$ restera sur cette hypersurface, nous pourrons le représenter par un point de l’espace ordinaire et nous serons affranchis de l’hypergéométrie.

Les surfaces d’intégration du type précédent sont très particulières, puisqu’elles sont situées sur l’image de $ \mathbb{R}^3_{\lambda, \mu, \nu}$ par une application rationnelle. Mais elles sont suffisantes pour le but de Poincaré pour la raison suivante :

Il est aisé de démontrer que toute surface d’intégration, ou bien est susceptible de ce mode de représentation, ou bien diffère très peu d’une surface qui en est susceptible, ou bien enfin peut être décomposée en plusieurs autres qui diffèrent très peu de surfaces algébriques admettant ce mode de représentation.

Nous voici face à des considérations menant directement à la notion d’homologie telle qu’il la définira dans l’« Analysis Situs ». En effet, si une surface diffère « très peu » d’une autre, les deux surfaces pourront se déformer l’une dans l’autre. En mettant bout à bout de telles déformations, on est amenés à déclarer équivalentes deux surfaces, même pas du tout proches l’une de l’autre, dès que l’on peut déformer l’une dans l’autre à l’aide d’un paramètre. Mais un chemin de déformation peut aboutir à une décomposition de la surface en plusieurs autres, éventuellement recouvertes plusieurs fois. Cela force à déclarer qu’une surface peut être équivalente à une somme formelle d’autres surfaces, avec des coefficients entiers : c’est pour une telle relation d’équivalence que Poincaré a introduit le terme d’homologie.

Le point-clè est qu’ici les surfaces d’intégration ne comptent qu’à homologie près. Et cela parce que les intégrales doubles qu’il considère vérifient des « conditions d’intégrabilité ».

Mais avant de passer à celles-ci, qui sont le sujet de la section II de l’article de 1887, précisons un point-clé sur les homologies à considérer dans ce contexte. Les intégrales étudiées par Poincaré sont de la forme :

$$ \int \int F(\xi, \eta) d \xi d\eta$$

où $F(\xi, \eta)$ est une fonction rationnelle des variables $\xi, \eta$. Si cette fonction est écrite sous forme irréductible, alors elle est définie en dehors des courbes algébriques définies par l’annulation des facteurs irréductibles du dénominateur. Topologiquement, ces courbes sont des surfaces, ayant éventuellement des points singuliers, et se coupant en général entre elles. Il s’agit pour Poincaré des « surfaces singulières » de l’intégrale. Les surfaces d’intégration doivent éviter ces surfaces singulières, et les homologies sont aussi à prendre en dehors de celles-ci.

Si l’homologie de $\mathbb{R}^4$ est triviale (toute surface fermée et orientée est homologue à zero), ce n’est pas le cas pour le complémentaire de la surface singulière, et c’est cela qui donnera naissance aux périodes et résidus que Poincaré définira par la suite.

Les « conditions d’intégrabilité »

Poincaré commence par rappeler les cas où les « conditions d’intégrabilité » étaient connues :

On sait ce qu’on doit entendre par une intégrale simple :

$$ \int(X dx + Y dy + Z dz)$$

prise le long d’une courbe gauche quelconque dans l’espace $(x,y,z)$. On connaît également les conditions d’intégrabilité : c’est-à-dire les conditions pour que l’intégrale soit indépendante du chemin d’intégration et ne dépende que des deux points extrêmes de ce chemin [...] Ces conditions sont :

$$ \frac{dX}{dy} = \frac{dY}{dx}, \frac{dX}{dz} = \frac{dZ}{dx}, \frac{dY}{dz} = \frac{dZ}{dy}. $$

Ces résultats s’étendent immédiatement, comme on le sait, au cas d’un espace d’un nombre quelconque de dimensions.

[Ensuite Poincaré explicite le cas des intégrales simples prises le long d’un chemin d’intégration dans $\mathbb{R}^n$.]

Passons maintenant au cas des intégrales doubles, et d’abord dans l’espace ordinaire. Soit une intégrale double

$$ \int \int (A dy dz + B dz dx + C dx dy)$$

$A, B$ et $C$ étant trois fonctions de $x, y, z$.

[Ensuite Poincaré explique comment calculer une telle expression une fois choisie une orientation de la surface.]

La condition d’intégrabilité (c’est-à-dire la condition pour que l’intégrale prise le long d’une surface fermée quelconque soit nulle) s’écrit alors

$$ \frac{dA}{dx} + \frac{dB}{dy} + \frac{dC}{dz} =0.$$

Le premier cas nouveau est celui des intégrales doubles dans des espaces $\mathbb{R}^n$ de dimension plus grande :

Soient $x_1, x_2, ..., x_n, n$ variables indépendantes. Désignons maintenant par la notation

$$ (X_i, X_k)$$

diverses fonctions données de ces $n$ variables. Nous supposerons que l’on a

$$ (X_i, X_i) =0, (X_k, X_i) = - (X_i, X_k).$$

Nous allons envisager l’intégrale double

$$J = \int \int \sum (X_i, X_k) dx_i dx_k$$

où l’on fait entrer sous le signe $\sum$ les $\frac{n(n-1)}{2}$ combinaisons des deux indices $i$ et $k$.

Après avoir expliqué à nouveau quel sens donner à l’intégrale précédente une fois choisie une orientation de la surface d’intégration, il formule une nouvelle fois le problème de l’intégrabilité :

Notre intégrale double étant ainsi complètement définie, il faut trouver les conditions d’intégrabilité ; je veux dire les conditions pour que l’intégrale ne dépende pas de la surface d’intégration, mais seulement de la courbe qui limite cette surface ; de même que les intégrales simples appliquées à des différentielles exactes ne dépendaient pas du chemin d’intégration, mais seulement des extrémités de ce chemin.

Sa démarche pour trouver ces conditions est la suivante :

 Il part d’une surface paramétrée par $x_i = \phi_i(u,v)$, où $(u,v)$ varie dans un domaine du plan $\mathbb{R}^2$ bordé par une courbe fermée.

 Il considère une déformation à un paramètre $w$ de la paramétrisation précédente : $x_i = \phi_i(u,v,w)$, ces fonctions étant indépendantes de $w$ le long du contour du domaine.

 Il impose que l’intégrale considérée $J$ prise sur ces diverses surfaces qui partagent le même bord soit constante ; ici $J$ désigne donc une fonction de $w$.

 Il calcule la dérivée de cette intégrale par rapport au paramètre de déformation :

$$ \frac{dJ}{dw} = \int \int \sum[ \frac{d(X_i, X_k)}{d x_h} + \frac{d(X_k, X_h)}{d x_i} + \frac{d(X_h, X_i)}{d x_k}] \frac{\partial(x_i, x_k, x_h)}{\partial (u,v,w)} du dv.$$

 Il en déduit que cette dérivée est nulle pour tous les choix de déformation $\phi(u, v, w)$ si et seulement si :

$$ \frac{d(X_i, X_k)}{d x_h} + \frac{d(X_k, X_h)}{d x_i} + \frac{d(X_h, X_i)}{d x_k} = 0.$$

Arrivé là, il conclut :

Telles sont les conditions d’intégrabilité. Il faut prendre pour le système des trois nombres $(i,k,h)$ toutes les combinaisons possibles, en excluant celles où deux des lettres seraient identiques et en ne regardant pas comme distinctes celles qui ne diffèrent que par l’ordre des lettres.

Poincaré n’utilise donc pas directement la définition des conditions d’intégrabilité, mais une conséquence de cette définition, le fait que l’intégrale est inchangée dans n’importe quelle variation de la surface d’intégration, c’est-à-dire famille à un paramètre de telles surfaces. Cela est une démarche typique de calcul des variations, qu’il connaissait bien grâce à son intérêt pour la mécanique céleste ou la physique en général.

Dans cet article il n’aura besoin que du cas où l’espace ambiant est de dimension (réelle) quatre. Mais il parle néanmoins aussi des intégrales multiples d’ordre supérieur, en écrivant les conditions d’intégrabilité pour les intégrales triples et quadruples, afin de faire percevoir que la règle des signes qui précèdent les diverses dérivées partielles qui les composent dépend de la parité de l’ordre d’intégration.

Les formules pour les conditions d’intégrabilité calculées dans cette section II de l’article de 1887 seront reprises sans preuves et pour des ordres d’intégration quelconques dans la section 7 de son article « Analysis Situs » de 1895 (voir à ce sujet nos commentaires de cette section).

Voyons à présent pourquoi Poincaré avait besoin des « conditions d’intégrabilité ».

« Théorème fondamental »

C’est là le titre de la section III de l’article de 1887. Il s’agit probablement de ce que Poincaré énonce ainsi dans le dernier paragraphe de la section :

On peut résumer tout ce qui précède en disant que l’intégrale prise le long d’une surface fermée $S$ ne dépend que des courbes singulières qui sont contenues à l’intérieur de cette surface.

Expliquons le contexte : on étudie l’intégrale double :

$$\int \int F(\xi, \eta) d \xi d \eta$$

dans laquelle $F(\xi, \eta)$ est une fraction rationnelle. Le lieu de ses pôles est constitué des « surfaces singulières » de l’intégrale. La surface d’intégration $S$ est contenue dans une « hypersurface » de l’espace ambiant $\mathbb{C}^2_{\xi, \eta} = \mathbb{R}^4_{x,y,z,t}$, et ne rencontre pas les surfaces singulières. Cette hypersurface peut par contre rencontrer les surfaces singulières le long de plusieurs « courbes singulières ». L’hypersurface étant paramétrée par $\mathbb{R}^3_{\lambda, \mu, \nu}$, on peut penser à la fois à $S$ et aux courbes singulières dans cet « espace ordinaire » $\mathbb{R}^3$. Cela a alors un sens de regarder lesquelles sont « contenues à l’intérieur » de $S$.

Ce théorème provient du fait qu’en dehors du lieu polaire de $F$, c’est-à-dire des surfaces singulières, l’intégrale double vérifie les conditions d’intégrabilité. C’est ce que prouve Poincaré dans la première partie de cette section, comme une conséquence du fait que $F$ est holomorphe séparément en chacune des variables $\xi$ et $\eta$, et qu’elle vérifie donc les équations de Cauchy-Riemann par rapport aux deux variables.

Remarquons à ce sujet un point délicat dans le traitement de la définition des conditions d’intégrabilité. En effet :

 Dans la section précédente, Poincaré définissait celles-ci comme les conditions pour que l’intégrale prise le long de n’importe quelle surface fermée soit nulle. Cette contrainte implique que sont vérifiées les équations qu’il a calculées. La réciproque est aussi vraie pourvu que l’intégrant soit défini sur $\mathbb{R}^n$ tout entier (ce qu’il ne démontre pas). Ceci est compréhensible si on pense que les ingrédients nécessaires n’allaient être élaborés petit à petit dans la généralité voulue qu’à la suite de son article de 1895 : la formule de Stokes généralisée et le fait que toute surface fermée de $\mathbb{R}^n$ est homologue à $0$, fait qui est automatique pour ses surfaces fermées contenues dans des espaces $\mathbb{R}^3$.

 Dans cette section Poincaré appelle « conditions d’intégrabilité » les équations trouvées dans la section précédentes. Par contre elles ne peuvent plus être définies de la même manière, puisque maintenant l’intégrant n’est défini qu’en dehors des surfaces singulières. En fait, les intégrales sur les surfaces fermées ne sont pas toutes nulles, et c’est précisément elles qui sont les « périodes » de l’intégrale, que Poincaré étudiera dans la section suivante. En fait, dans ce nouveau contexte les conditons d’intégrabilité sont équivalentes au fait que l’intégrale prise sur une surface fermée ne dépend que de la classe d’homologie de la surface. Mais là aussi il allait falloir développer les bases posées par Poincaré dans son article de 1895 pour arriver à avoir une preuve complète de ce fait.

Revenons à $\mathbb{R}^3$, à la surface d’intégration qu’elle contient et à ses courbes singulières. Le fait que les condition d’intégrabilité soient vérifiées en dehors de ces dernières montre que l’intégrale double calculée le long de la surface d’intégration est égale à l’intégrale double prise le long de n’importe quelle surface qui lui est homologue en dehors de ces courbes. En entourant chacune des courbes qu’elle contient par une surface torique, la surface initiale est homologue à la somme de ces tubes (convenablement orientés). Et c’est précisément à de tels tubes que Poincaré se ramènera par la suite, comme nous l’expliquerons plus bas.

Les périodes des intégrales doubles

Le terme de « période » désignait avant les années 1880 une intégrale d’une forme holomorphe prise le long d’une courbe fermée et orientée tracée sur une surface de Riemann. Les équations de Cauchy-Riemann garantissant que les « conditions d’intégrabilité » sont remplies, on savait depuis les travaux de Riemann des années 1850 que l’intégrale ne dépendait que de la classe d’homologie de la courbe.

L’un des apports de Poincaré dans l’article que nous étudions est terminologique : il y étend le terme de « période » aux intégrales doubles. Dégageons cette définition, dans son langage :

Pour lui, le point essentiel que l’on doit respecter lorsque l’on cherche à étendre ce terme du cas des surfaces de Riemann aux dimensions plus grandes, est de préserver cette propriété d’invariance homologique. Voici comment il explique cela dans l’introduction de son article, en partant d’une intégrale double écrite quelques années auparavant par Picard :

M. Picard a donné à ces intégrales le nom de périodes ; je ne saurais l’en blâmer puisque cette dénomination lui a permis d’exprimer dans un langage plus concis les intéressants résultats auxquels il est parvenu. Mais je crois qu’il serait fâcheux qu’elle s’introduisit définitivement dans la Science et qu’elle serait propre à engendrer de nombreuses confusions.

Et cela pour deux raisons :

D’abord ces intégrales ne sont pas des constantes, comme le fait fort bien observer M. Picard.

En second lieu, il y a une infinité de systèmes de variables auxiliaires $u$ et $v$ qui satisfont aux conditions énoncées. Chacun de ces systèmes donne pour l’intégrale une valeur différente. Il en résulterait que, si l’on voulait donner à cette intégrale le nom de période, cette période ne dépendrait pas uniquement de la fonction $F(x,y)$ à laquelle elle appartient, mais bien de ces variables soi-disant auxiliaires qui joueraient ainsi un rôle prépondérant.

Poincaré se propose donc de trouver les périodes de l’intégrale double considérée. Il a déjà affirmé, comme expliqué plus haut, que ces périodes sont des combinaisons linéaires à coefficients entiers de périodes calculées le long de surfaces du type spécial qu’il considère, contenues dans des hypersurfaces paramétrées par $\mathbb{R}^3$. Quant à ce type de périodes restreint, il peut être à son tour ramené à des périodes encore plus spéciales :

Supposons que la surface $S$ contienne à son intérieur plusieurs courbes singulières fermées, par exemple deux que j’appellerai $C$ et $C'$. Nous pourrons toujours construire dans l’espace $(\lambda, \mu, \nu)$ deux surfaces fermées $\Sigma$ et $\Sigma'$ situées toutes deux à l’intérieur de $S$ et contenant à leur intérieur, la première $C$ et $C$ seulement, la seconde $C'$ et $C'$ seulement ; l’intégrale prise le long de $S$ sera alors la somme de l’intégrale prise le long de $\Sigma$ et de l’intégrale prise le long de $\Sigma'$, l’observateur $O$ qui définit le sens d’intégration demeurant toujours dirigé vers l’extérieur.

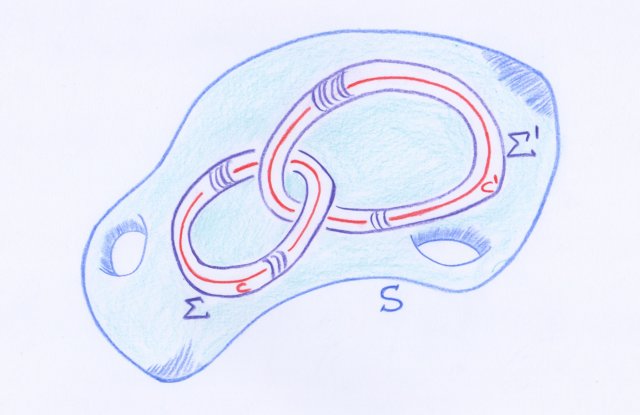
Profitons de cette dernière phrase pour préciser que Poincaré définit partout dans cet article les orientations des surfaces de l’espace $\mathbb{R}^3$ à l’aide de tels observateurs, et qu’il prend de nombreuses fois le temps d’expliquer comment gérer les orientations dans ses calculs d’intégrales multiples. Cela est important, puisqu’un changement d’orientation de la surface d’intégration entraîne un changement de signe de l’intégrale.

Le paragraphe précédent peut être vu comme l’un des prototypes de la théorie de l’homologie qu’allait définir Poincaré en 1895. En effet, la période le long de $S$ est la somme de la période le long de $\Sigma$ et de celle le long de $\Sigma'$ parce que $S$ est homologue à la somme $\Sigma + \Sigma'$ (une fois les surfaces convenablement orientées), et cela parce que prises ensemble, elles forment la « frontière complète » (expression de 1895) de la variété de dimension trois qu’elles délimitent dans $\mathbb{R}^3$.

Généralisations de la formule des résidus

Poincaré affirme ensuite comme un fait intuitivement évident que :

Toutes les surfaces $S$ renfermant la courbe $C$ conduiront à la même intégrale.

En choisisant une hypersurface particulière contenant $C$, puis un tore qui « enveloppe manifestement la courbe » $C$, il montre que la période associée à ce tore est égale à la période d’une intégrale simple le long de $C$, cette intégrale simple étant associée à la surface singulière contenant $C$ de l’intégrale double initiale.

Il arrive au théorème explicite suivant, énoncé pour le cas particulier où $F= \frac{P}{RQ}$, avec $P, Q, R$ polynômes deux à deux premiers entre eux :

Ainsi les périodes de l’intégrale double

$$\int \int \frac{P d\xi d \eta}{RQ}$$

sont les mêmes que celles de l’intégrale simple abélienne

$$ J = \int \frac{2i \pi P d \xi}{R \frac{dQ}{d \eta}}$$

relative à la courbe algébrique $Q =0$ et aussi que celles de l’intégrale simple abélienne

$$ J' = \int \frac{2i \pi P d \xi}{Q \frac{dR}{d \eta}}$$

relative à la courbe algébrique $R =0$.

Les périodes de l’intégrale double initiale le long de tores qui « enveloppent » les courbes $C$ sont donc des périodes d’intégrales simples prises le long des courbes complexes (les « surfaces singulières ») contenues dans le lieu des pôles de la fraction rationnelle considérée. Cela est analogue au fait, découvert par Cauchy, que si $f(z)$ est une fraction rationnelle à pôles simples, alors une période de l’intégrale simple :

$$\int f(z) dz$$

calculée le long d’un cercle $C_p$ qui « enveloppe » le pôle $p$ de $f(z)$, peut se calculer ainsi :

$$ \int_{C_p} f(z) dz = 2 i \pi [(z-p) f(z)](p).$$

Le nombre complexe $[(z-p) f(z)](p)$ est le « résidu » de $f(z)$ en $p$, raison pour laquelle la formule précédente est appelée « formule des résidus ».

C’est probablement pour cette raison que le titre de cette section IV de l’article de Poincaré est « Résidus des fonctions rationnelles ». Même s’il ne l’explique pas, on peut penser que les « résidus » dont il est question sont, à $2i \pi$ ou $(2i \pi)^2$ près, les intégrales simples $J$ et $J'$ du théorème précédent. Et que ce théorème constituait pour Poincaré une généralisation de la formule des résidus de Cauchy.

Certaines des courbes $C$ portées par la courbe polaire définie par $Q =0$ enveloppent un point singulier du lieu polaire de $F$. Poincaré ne considère que la situation dans laquelle en chacun de ces points singuliers il n’y a que deux composantes irréductibles analytiques de la courbe $RQ =0$ qui passent, toutes les deux lisses et se coupant transversalement. La période de l’intégrale simple le long de $C$ peut alors s’exprimer à l’aide de la formule de Cauchy le long de $Q=0$, au voisinage de ce point singulier. Poincaré obtient dans ce cas deux formules, que l’on peut voir aussi comme des généralisations de la formule des résidus de Cauchy :

Les pôles de l’intégrale $J$ sont les points d’intersection des deux courbes

$$ R=0, \: Q=0 $$

et les points doubles de la courbe $Q=0$.

Pour les premiers, le résidu est facile à calculer. On trouve que la période est égale à

$$ - 4 \pi^2 \frac{P}{\frac{dQ }{d \eta} \frac{dR }{d \xi} - \frac{dQ }{d \xi} \frac{dR }{d \eta} }$$

où $\xi, \eta$ sont remplacés par les coordonnées du point d’intersection considéré.

Si l’on considère ce même point d’intersection comme un pôle de l’intégrale $J'$, on est conduit au même résultat, au signe près.

Pour les points doubles de $Q=0$, on trouve :

$$ - 4 \pi^2 \frac{P}{R\sqrt{(\frac{d^2Q }{d \xi d \eta})^2 - \frac{d^2Q }{d \xi^2} \frac{d^2R }{d \eta^2} } }$$

où $\xi$ et $\eta$ sont remplacés par les coordonnées du point double.

Précisons que ces deux valeurs peuvent être calculées en prenant comme surface d’intégration un petit tore au voisinage du point double considéré, qui évite les surfaces singulières, dont le système de méridien entoure l’une des deux surfaces présentes au voisinage de ce point et le système de parallèles entoure l’autre.

Poincaré s’intéresse ensuite au « nombre de périodes indépendantes » de l’intégrale initiale, c’est-à-dire rationnellement indépendantes. En considérant le cas spécial où la fraction rationnelle a un dénominateur sans facteurs multiples, et définissant une courbe algébrique ayant uniquement des singularités du type précédent, il obtient :

Voici donc ce que nous pourrons dire en général :

Soient $p$ le degré du dénominateur, $\nu$ le nombre de ses facteurs irréductibles, $d$ le nombre des points doubles, le nombre des périodes sera :

$$ p^2 - 3 p + 2 \nu - d.$$

Ce nombre peut se réduire dans certains cas particuliers.

Il est important de comprendre ici sur quels objets porte cette dichotomie général/particulier. Poincaré ne précise rien à ce sujet. Mais, au vu de ce qu’il allait écrire dans la section 7 de son article « Analysis Situs », il s’agit de la fraction rationnelle, son lieu polaire étant considéré fixé. Il suppose probablement que pour un numérateur générique, les diverses périodes sont rationnellement indépendantes, et qu’elles ne deviennent dépendantes que pour des valeurs spéciales des coefficients de ce numérateur.

Précisons que les considérations de cette section IV de l’article de 1887 peuvent être vues comme un prototype des questions allant mener au théorème de dualité d’Alexander, que ce dernier prouva en 1922 [2]. En effet, ce théorème explique comment l’homologie d’un sous-espace contenu dans $\mathbb{R}^n$ détermine l’homologie de son complémentaire. Mais c’est ce que Poincaré a cherché à faire dans son article sur les résidus des intégrales doubles, en montrant comment l’homologie de dimension $2$ du complémentaire du lieu polaire de $F$ est déterminée par l’homologie de dimension $1$ de ce lieu polaire.

Poincaré continue son article en expliquant ce qui se passe lorsque le dénominateur de $F$ admet des facteurs multiples, puis il donne plusieurs applications de ses formules de résidus. Mais nous nous arrêterons ici de nos commentaires, dans lesquels nous avons uniquement voulu expliquer les aspects de cet article qui forment un prélude à l’« Analysis Situs ».

Les lecteurs désireux de découvrir un point de vue moderne sur la théorie des résidus pourront consulter l’article « Introduction to residues and resultants » de Cattani et Dickenstein [3].