Des diagrammes de Listing à ceux de Heegaard

De nos jours, on appelle « diagrammes de Heegaard » une manière de présenter les variétés fermées et orientables de dimension $3$ à l’aide d’un dessin fait dans un plan. De tels diagrammes sont associés à une « décomposition de Heegaard » de la variété : une surface plongée la découpant en deux « corps en anses » et un ensemble fini de disques deux à deux disjoints dans chaque corps en anses, tel que si on découpe chaque corps en anses le long de ces disques, on obtient une boule de dimenson $3$. Le diagramme de Heegaard est obtenu en dessinant sur la sphère qui borde l’une de ces boules les bords des disques que l’on doit identifier pour reconstruire le corps en anses associé, ainsi que les arcs qui proviennent des bords des disques du deuxième corps en anses.

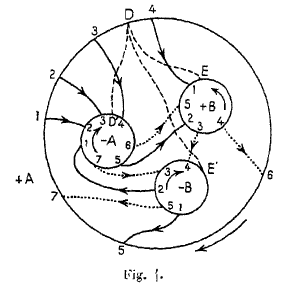
C’est grâce à un tel diagramme de Heegaard (qu’il n’a pas appelé de la sorte) que Poincaré a construit sa célèbre sphère d’homologie :

Heegaard lui-même n’a pas introduit les diagrammes qui portent son nom, mais presque. Il a introduit dans [1] d’autres « diagrammes », en empruntant le terme à Listing, qui l’avait utilisé dans [2] pour décrire certains « complexes » de dimension $2$, plongés dans l’espace euclidien tridimensionnel. Les « diagrammes » introduits par Heegaard généralisent la construction de Listing à la dimension $3$, et Heegaard remarque que l’on peut aisément leur associer ce que l’on appelle de nos jours une « décomposition de Heegaard ».

Le but de ce texte est d’analyser ces aspects des travaux de Listing et Heegaard.

Listing est le créateur du terme de « topologie » (voir la Section I.1 de la Seconde Partie du livre de Pont [3]). Il publia d’ailleurs en 1847 le premier livre [4] consacré à ce sujet, qui présentait une panoplie de problèmes à rattacher, selon lui, à cette nouvelle branche des mathématiques.

Quelques années plus tard il écrivit l’article [5] dans lequel il se proposait de créer le vocabulaire et les méthodes de base permettant de décrire les figures de dimension au plus $2$ de l’espace tridimensionnel. Il appela ces figures des « complexes spatiaux ». Listing les définit de la manière suivante (nous citons des extraits traduits par Pont ; c’est nous qui mettons l’expression définie en évidence) :

« Par complexe spatial, nous entendrons toute configuration de points, lignes et surfaces dans l’espace ; les lignes et les surfaces pouvant à volonté être droites ou courbes, ouvertes ou fermées, limitées ou illimitées. On demandera toutefois qu’elles soient d’un seul tenant, sans quoi on comptera autant de complexes qu’il y aura de configurations distinctes. Nous prendrons également en considération le complexe ne contenant aucun élément. »

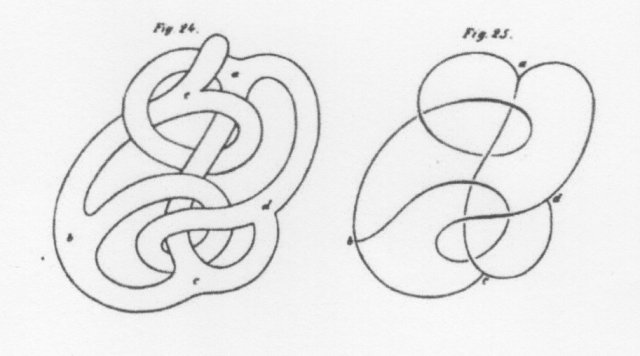
Les complexes sont formés de « constituants », qui sont des points, des arcs, des surfaces ou des portions d’espace tridimensionnel. Ce sont les surfaces qui sont les plus compliquées à décrire avec leur plongement dans l’espace. Listing propose de le faire en les rétractant par déformation sur un « squelette », qui est un graphe plongé dans la surface qu’il appelle le « diagramme » de celle-ci :

« Soit $K$ un constituant et $L$ sa frontière ; faisons subir à $L$ une variation continue, de manière à ce qu’elle pénètre de plus en plus à l’intérieur de $K$, afin que seul reste de celui-ci un complexe formé de points et de lignes. On déduit ainsi de $K$ un complexe linéaire que l’on peut considérer comme le squelette du complexe donné. Nous appelons diagramme cyclomatique ou simplement diagramme de $K$ le complexe linéaire obtenu par la transformation précédente de la frontière $L$. »

C’est nous qui avons traduit la dernière phrase. L’attribut « cyclomatique » provient du fait que Listing pense à ce graphe comme un codage des divers cycles qui peuvent être tracés non-trivialement dans la surface.

Voici deux des figures de l’article de Listing, illustrant les explications précédentes :

Le même procédé de rétraction par déformation est décrit par Betti dans ses lettres à Tardy qui racontent des discussions avec Riemann, analysées dans ce commentaire. Leur contexte est un peu différent : il s’agit de mesurer l’« ordre de connexion » d’une variété de dimension $3$. Elles sont aussi postérieures de deux ans au travail de Listing. Mais, Listing et Riemann se trouvant tous deux à Göttingen, il semble difficile de croire qu’ils ne se sont pas influencés à ce sujet. Discussions lors de promenades, exposés de séminaires ? En l’état actuel des connaissances, nous ne pouvons rien dire de précis sur la manière dont cette idée d’utiliser des rétractions par déformation sur des objets de dimension inférieure pour analyser la structure topologique
des espaces s’est faite jour et a commencé à se propager.

Le lecteur pourra trouver d’autres détails sur ce travail de Listing dans la Section I.3 de la Seconde Partie du livre de Pont.

Venons-en au travail de Heegaard. Le problème qui le mène à introduire un « diagramme » associé à une variété de dimension $3$ est le même que chez Riemann et Betti, c’est-à-dire celui de rendre une variété « simplement connexe » par coupures successives. Ici la « simple connexité » est prise au sens de Riemann : toute sous-variété fermée y borde. C’est ce problème qui le mène à introduire un diagramme analogue à celui de Listing, mais pour une variété de dimension $3$ (voir la Section VII de son article) :

« La question que nous rencontrons d’abord est celle-ci : quelles sont les coupures que l’on doit faire pour rendre une variété fermée [...] simplement connexe ? Pour résoudre cette question nous ferons usage du procédé suivant : on perce la variété, c’est-à-dire on enlève la variété élémentaire qui forme le voisinage d’un point. On créé ainsi une frontière que l’on élargit par une déformation continue de façon à enlever de plus en plus de la variété donnée. On continue ainsi jusqu’à ce que certaines parties de la frontière se rapprochent d’autres, en arrêtant la transformation en ces endroits lorsque la distance entre les parties qui se rencontrent est devenue infiniment petite. En poursuivant ainsi, on est conduit à un diagramme formé d’un système de variétés de dimensions inférieures à celle de la variété donnée, ou plutôt formé par le voisinage de ce système, c’est-à-dire par une variété qui, dans la $n$-ème dimension est infiniment petite. »

Apparaît néanmoins une différence par rapport aux diagrammes de Listing, ainsi qu’à leurs analogues en dimension supérieure mentionnés dans la deuxième lettre de Betti à Tardi, puis dans l’article de Betti : le « diagramme » introduit par Heegaard est plutôt un voisinage tubulaire du diagramme selon Listing. Cela est précisé dans le paragraphe suivant :

« Considérons maintenant le diagramme lui-même. Chaque point de jonction est entouré d’une variété élémentaire (un élément de volume) à laquelle nous pourrons donner par exemple la forme sphérique ; les arcs de courbe reliant les sphères sont entourés d’espaces filiformes attachés aux surfaces sphériques par des petits éléments de surface. Appelons ces espaces des fils ; ils peuvent être tracés par un élément de surface se déplaçant d’une des surfaces sphériques à l’autre ; ceci peut se faire, d’ailleurs, de deux façons essentiellement différentes [...]

L’espace entourant un élément de surface du diagramme est un espace en forme de plaque limité par deux éléments de surface formant les côtés de la plaque et par une surface en forme de bande de même connexion qu’un anneau circulaire, et qui forme le bord de la plaque. Cet espace, que nous appellerons une plaque, est attaché le long de son bord à une bande appartenant à la surface de la variété formée par les fils et les sphères aux points de jonction des fils. »

Illustrons ces explications de Heegaard par une figure :

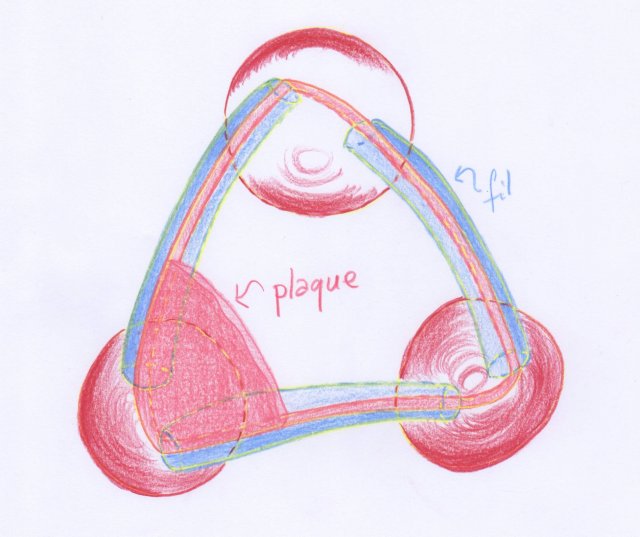
Par rapport aux écrits de Riemann et Betti, on voit que Heegaard s’occupe aussi des questions d’orientabilité. C’est de cela qu’il s’agit lorsqu’il mentionne qu’un « élément de surface » (c’est-à-dire un petit disque) peut aller d’une surface sphérique à une autre « de deux façons essentiellement diférentes ». Il reviendra sur cet aspect dans une section ultérieure, après avoir consacré une section séparée à divers points de vue intuitifs sur la manière d’orienter une variété.

Arrivés à ce point, nous reconnaissons un premier « corps en anses » au sens moderne, dans le cas où la variété de départ est orientable. Il s’agit de l’union des boules (« éléments de volume ») et des « fils » qui les joignent. Afin de reconstruire la variété initiale, il faut dire comment se recollent les « plaques » (des cylindres pleins) le long de la partie annulaire de leur bord. Mais seulement certains recollements sont possibles, ceux pour lesquels le nouveau bord est homéomorphe à une sphère. Heegaard décrit cette situation de la manière suivante, via l’effet produit sur le bord du corps en anses par des coupures pratiquées le long des anneaux d’attachement des plaques (c’est lui qui écrit en italiques) :

« La condition nécessaire et suffisante pour qu’un tel système de fils, avec des courbes d’attachement pour des plaques, puisse représenter le diagramme d’un espace fermé est celle-ci : que les courbes d’attachement soient formées par $p$ coupures fermées qui laissent la surface du système de fils connexe. »

C’est dans ce paragraphe que l’on se trouve le plus près de la version moderne des « diagrammes de Heegaard ». Et un peu plus loin, dans la Section XI, on trouve aussi la description de la variété fermée initiale comme union de deux corps en anses, c’est-à-dire munie d’une « décomposition de Heegaard » :

« Si l’on ferme le diagramme en rattachant sa surface à celle d’une sphère, on obtient, comme nous l’avons dit, une variété équivalente à la variété donnée. Les parties peuvent d’ailleurs être séparées d’une façon un peu différente ; au lieu de joindre les plaques au système de fils, on peut les joindre de leurs deux côtés à la surface de la sphère. On obtient ainsi un corps à $p$ anses, tout à fait semblable au système de fils. La surface de ce corps se joint à la surface du système de fils ; il suffit de connaître sur la surface du corps le système de coupures annulaires (ne morcelant pas la surface) correspondant aux courbes $\beta$ sur la surface du système de fils, et le système correspondant aux courbes $\lambda$. »

Les « courbes $\beta$ » et les « courbes $\lambda$ » sont les méridiens et les parallèles à la surface des tores pleins, dans une présentation du corps en anses formé par les boules et le « système de fils » qui les joignent comme somme connexe d’une boule et de plusieurs tores pleins. Cette information est redondante : il suffit de connaitre seulement la moitié de ces courbes, celles qui bordent à l’intérieur du corps en anses. Comme nous l’avons rappelé au début de ce texte, le « diagramme de Heegaard » au sens moderne s’obtient immédiatement à partir de deux tels systèmes de courbes, un pour chacun des deux corps en anses de la décomposition.

Heegaard conclut les sections consacrées à cette présentation « diagrammatique » des variétés de dimension $3$ par une remarque sur les difficultés que l’on rencontre si l’on veut étendre cette théorie en dimension plus grande :

« Mentionnons aussi une circonstance qui rend la théorie plus difficile dans le cas où le nombre de dimensions dépasse $2$. Si sur le diagramme d’une surface fermée bilatère on tranche une anse, la jonction après coup ne peut se faire essentiellement que d’une seule façon si la surface doit rester bilatère ; on revient donc, sans doute, en refaisant la jonction, à un diagramme équivalent au premier. Si, par contre, on a une variété à $3$ dimensions, comme celle qui constitue la frontière du voisinage d’un tore dans $\mathbf{T}$, cette variété pourra être tranchée par un tore (correspondant à une courbe méridienne sur une surface dont on examine l’enveloppe). Cependant, la jonction peut se refaire de façons infiniment nombreuses et essentiellement différentes [...]. »

Apparaît ici le problème de l’étude du groupe des difféotopies des variétés de dimension au moins $2$, source de complication dans la description des variétés par recollements de morceaux plus simples. Ce sont les générations suivantes qui aborderont cette étude.