Comment Poincaré présentait l’Analysis Situs au "grand public"

Henri Poincaré était très sensible à ce qu’on appellerait aujourd’hui la « diffusion des mathématiques ». Très souvent il accompagnait ses articles difficiles par d’autres articles destinés à un public plus large. Ses quatre livres de philosophie des sciences ont eu un succès incroyable. Sur cet aspect, nous recommandons l’article de L. Rollet intitulé Henri Poincaré - Vulgarisation scientifique et philosophie des sciences.

En ce qui concerne la topologie algébrique, voici le début d’une conférence de Henri Poincaré, publiée dans son livre Dernières pensées, et intitulée Pourquoi l’espace a trois dimensions.

Les géomètres distinguent d’ordinaire deux sortes de géométries, qu’ils qualifient la première de métrique et la seconde de projective.

La géométrie métrique est fondée sur la notion de distance ; deux figures y sont regardées comme équivalentes, lorsqu’elles sont « égales » au sens que les mathématiciens donnent à ce mot.

La géométrie projective est fondée sur la notion de ligne droite. Pour que deux figures y soient considérées comme équivalentes, il n’est pas nécessaire qu’elles soient égales, il suffit qu’on puisse passer de l’une à l’autre par une transformation projective, c’est-à-dire que l’une soit la perspective de l’autre. On a souvent appelé ce second corps de doctrine, la géométrie qualitative. Elle l’est en effet si on l’oppose à la première, il est clair que la mesure, que la quantité y jouent un rôle moins important. Elle ne l’est pas entièrement cependant. Le fait pour une ligne d’être droite n’est pas purement qualitatif ; on ne pourrait s’assurer qu’une ligne est droite sans faire des mesures, ou sans faire glisser sur cette ligne un instrument appelé règle qui est une sorte d’instrument de mesure.

Mais il est une troisième géométrie d’où la quantité est complètement bannie et qui est purement qualitative ; c’est l’Analysis Situs. Dans cette discipline, deux figures sont équivalentes toutes les fois qu’on peut passer de l’une à l’autre par une déformation continue, quelle que soit d’ailleurs la loi de cette déformation pourvu qu’elle respecte la continuité. Ainsi un cercle est équivalent à une ellipse ou même à une courbe fermée quelconque, mais elle n’est pas équivalente à un segment de droite parce que ce segment n’est pas fermé ; une sphère est équivalente à une surface convexe quelconque ; elle ne l’est pas à un tore parce que dans un tore il y a un trou et que dans une sphère il n’y en a pas. Supposons un modèle quelconque et la copie de ce même modèle exécutée par un dessinateur maladroit ; les proportions sont altérées, les droites tracées d’une main tremblante ont subi de fâcheuses déviations et présentent des courbures malencontreuses. Du point de vue de la géométrie métrique, de celui même de la géométrie projective, les deux figures ne sont pas équivalentes ; elles le sont au contraire du point de vue de l’Analysis Situs.

L’Analysis Situs est une science très importante pour le géomètre ; elle donne lieu à une série de théorèmes, aussi bien enchaînés que ceux d’Euclide ; et c’est sur cet ensemble de propositions que Riemann a construit une des théories les plus remarquables et les plus abstraites de l’analyse pure. Je citerai deux de ces théorèmes pour en faire comprendre la nature : deux courbes fermées planes se coupent en un nombre pair de points ; si un polyèdre est convexe, c’est-à-dire si on ne peut tracer une courbe fermée sur sa surface sans la couper en deux, le nombre des arêtes est égal à celui des sommets, plus celui des faces, moins deux ; et cela reste vrai quand les faces et les arêtes de ce polyèdre sont courbes.

Et voici ce qui fait pour nous l’intérêt de cette Analysis Situs ; c’est que c’est là qu’intervient vraiment l’intuition géométrique. Quand, dans un théorème de géométrie métrique, on fait appel à cette intuition, c’est parce qu’il est impossible d’étudier les propriétés métriques d’une figure en faisant abstraction de ses propriétés qualitatives, c’est-à-dire de celles qui sont l’objet propre de l’Analysis Situs. On a dit souvent que la géométrie est l’art de bien raisonner sur des figures mal faites. Ce n’est pas là une boutade, c’est une vérité qui mérite qu’on y réfléchisse. Mais qu’est-ce qu’une figure mal faite ? c’est celle que peut exécuter le dessinateur maladroit dont nous parlions tout à l’heure ; il altère les proportions plus ou moins grossièrement ; ses lignes droites ont des zigzags inquiétants ; ses cercles présentent des bosses disgracieuses ; tout cela ne fait rien, cela ne troublera nullement le géomètre, cela ne l’empêchera pas de bien raisonner. Mais il ne faut pas que l’artiste inexpérimenté représente une courbe fermée par une courbe ouverte, trois lignes qui se coupent en un même point par trois lignes qui n’aient aucun point commun, une surface trouée par une surface sans trou. Alors on ne pourrait plus se servir de sa figure et le raisonnement deviendrait impossible. L’intuition n’aurait pas été gênée par les défauts de dessin qui n’intéressaient que la géométrie métrique ou projective ; elle deviendra impossible dès que ces défauts se rapporteront à l’Analysis Situs. Cette observation très simple nous montre le véritable rôle de l’intuition géométrique ; c’est pour favoriser cette intuition que le géomètre a besoin de dessiner des figures, ou tout au moins de se les représenter mentalement. Or, s’il fait bon marché des propriétés métriques ou projectives ces figures, s’il s’attache seulement à leurs propriétés purement qualitatives, c’est que c’est là seulement que l’intuition géométrique intervient véritablement. Non que je veuille dire que la géométrie métrique repose sur la logique pure, qu’il n’y intervienne aucune vérité intuitive ; mais ce sont des intuitions d’une autre nature, analogues à celles qui jouent le rôle essentiel en arithmétique et en algèbre.

Bien entendu, nous recommandons la lecture (et même l’écoute !) de la suite de cette conférence remarquable.

Un exercice : Démontrez le théorème énoncé par Poincaré : « deux courbes fermées dans le plan se coupent un nombre pair de fois ». Bien entendu, énoncé comme cela, il est faux (et il faut s’habituer à ce genre d’énoncés « presque vrais » en lisant Poincaré). Par exemple, deux cercles tangents en un point se coupent... en un seul point ! Pour énoncer un théorème correct, on considère deux applications lisses $f_1,f_2$ du cercle ${\mathbb R}/ {\mathbb Z}$ dans le plan ${\mathbb R}^2$. On ne suppose pas que les $f_i$ sont injectives, de sorte que les courbes peuvent se recouper. En revanche, on suppose que les deux courbes sont transverses, ce qui signifie qu’en chaque point d’intersection de $f_1$ avec $f_2$, les deux vecteurs tangents en ces points sont linéairement indépendants. Alors, il s’agit de montrer que le nombre de ces points d’intersection entre $f_1$ et $f_2$ est pair.

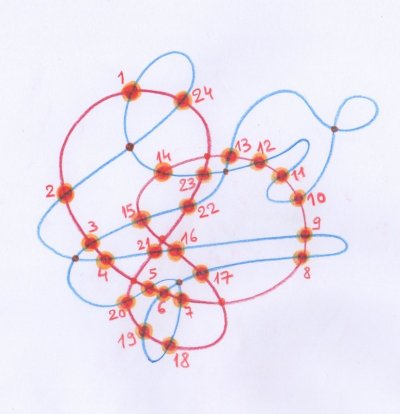
Un deuxième exercice : Dessinez une courbe fermée et immergée $f: {\mathbb R}/ {\mathbb Z} \to {\mathbb R}^2$ dans le plan (c’est-à-dire que sa dérivée est partout non nulle). On suppose que la courbe n’a pas de points triples et qu’aux points d’auto intersection les tangentes sont linéairement indépendantes. Démontrez qu’on peut noircir certaines des composantes connexes du complémentaire, de telle sorte que deux composantes adjacentes quelconques aient des couleurs différentes.