Les exemples de Poincaré
L’Analysis Situs et ses cinq compléments sont l’occasion, pour Poincaré, d’introduire de nombreux exemples de variétés, la plupart de dimension 3.
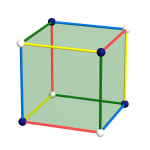
Dès le paragraphe 10 de l’Analysis Situs, Poincaré propose une méthode générale de construction de variétés comme recollement de polyèdres. [1] Il considère en particulier cinq exemples où le polyèdre est un cube. Nous étudions de manière systématique tous ces recollements dans une rubrique dédiée. On détermine en particulier ceux d’entre eux qui définissent une variété, et on identifie alors le type topologique.
Dans le paragraphe 11 [2] Poincaré considère une sixième famille d’exemples : les suspensions d’homéomorphismes linéaires du tore. Cette famille d’exemples a la particularité de n’être pas classifiée par ses groupes d’homologie. L’étude des surfaces complexes (donc de dimension réelle $4$) dans les troisième et quatrième compléments conduiront ensuite Poincaré à s’intéresser aux suspensions d’homéomorphismes de surfaces de genre quelconque. Nous consacrons une rubrique à ces exemples.
Poincaré revient sur la topologie de dimension $3$ dans le cinquième complément à l’Analysis Situs, Il y construit une variété qui a la propriété d’avoir les mêmes groupes d’homologie à coefficients entiers que la 3-sphère, mais qui n’est pas homéomorphe à la 3-sphère. Une variété satisfaisant cette propriété est appelée sphère d’homologie entière. Poincaré la définit comme le recollement de deux corps en anses de genre 2, une construction appelée maintenant scindement de Heegaard. On peut donner de nombreuses autre description de cette magnifique variété, en particulier comme espace d’identification d’un dodécaèdre. Nous consacrons donc à cette seule variété une grande rubrique richement illustrée.
Autres exemples
Nous présentons aussi dans cette rubrique des exemples de variétés de dimension $3$ qui ne sont pas directement issus de l’Analysis Situs, mais qui prolongent les thèmes abordés dans les travaux de Poincaré.
Un autre recollement du dodécaèdre
Curieusement, Poincaré n’a pas cherché à étendre son étude des recollements du cube aux recollements du dodécaèdre, ce qui lui aurait permis de décrire autrement sa sphère d’homologie. Un autre espace d’identification du dodécaèdre, combinatoirement très proche de celui donnant la sphère d’homologie de Poincaré, donne quant à lui un des premiers exemples de variété de dimension 3 compacte homéomorphe à un quotient de l’espace hyperbolique par un groupe kleinéen : la variété de Seifert—Weber. Nous lui consacrons une rubrique.
Des variétés caractérisées (ou non) par leur groupe fondamental
Emporté par l’enthousiasme d’avoir inventé le groupe fondamental, Poincaré, dans la Note de 1892, s’emballe en annonçant que deux variétés ayant des groupes fondamentaux isomorphes sont homéomorphes ! On peut penser qu’il avait en tête des variétés compacte sans bord de dimension 3. [3] Il reste que même en dimension 3 ce « résultat » est faux. Il y a toutefois peu de contre-exemples : ce sont des espaces lenticulaires. Ces espaces illustrent bien les notions de scindement de Heegaard et de chirurgie de Dehn. Nous leur consacrons une rubrique.
En revanche, les fibrés en cercles au dessus d’une surface sont classifiés par leur groupe fondamental. Ces variétés font partie de la classe plus large des fibrés de Seifert, dont la classification et la géométrisation ont été une étape importante de la compréhension des $3$-variétés. Une rubrique leur est consacrée.
D’autres sphères d’homologie
Les Sphères de Brieskorn forment une magnifique famille de variétés de dimension 3. Elles ont été introduites bien plus tardivement dans un contexte — la théorie des singularités — qui aurait certainement passionné Poincaré. Ce sont encore des fibrés de Seifert. Elles fournissent surtout une riche famille de sphères d’homologie parmi lesquelles on retrouve la sphère d’homologie de Poincaré. Tout ceci méritait bien qu’on lui consacre une rubrique.
Des outils pour construire encore plus de $3$-variétés
Un théorème d’Alexander affirme que que toute variété compacte orientable et de dimension 3 est un revêtement ramifié de l’hypersphère $\mathbb{S}^3$. Les revêtements ramifiés sont donc une très riche source d’exemples de dimension 3. Dans la rubrique Revêtements ramifiés nous expliquons cette technique et nous revisitons les exemples rencontrés à la lumière de ce nouvel éclairage dans l’article :
Enfin, pour bien comprendre tous les exemples de cette rubrique, quelques rappels de topologie peuvent être nécessaires. Nous les avons rassemblé dans une rubrique :
[1] Voir l’article Espaces d’identification et 3-variétés pour une description moderne de cette construction.
[2] Et même plus tôt dans la Note de 1892.