Exemples de revêtements ramifiés en dimension 3

En dimension $3$, le lieu de ramification d’un revêtement ramifié est une courbe. En particulier, on peut construire des variétés de dimension $3$ non triviales comme des revêtements ramifiés de la sphère $\mathbb{S}^3$ le long d’un entrelac.

Les sphères de Brieskorn

Soient $p,q,r$ trois entiers premiers entre eux. La sphère de Brieskorn $\Sigma(p,q,r)$ est l’intersection dans $\mathbb{C}^3$ de la sphère $\mathbb{S}^5$ avec la surface complexe d’équation $z_1^p+z_2^q+z_3^r=0$.

L’application $f:\Sigma(p,q,r)\to \mathbb{S}^3$ définie par

$$f(z_1,z_2,z_3)=(\frac{z_1}{\sqrt{|z_1|^2+|z_2|^2}},\frac{z_2}{\sqrt{|z_1|^2+|z_2|^2}})$$

est un revêtement d’ordre $r$ qui ramifie $r$ fois au dessus de la courbe d’équation

$$z_1^p+z_2^q=0~.$$

Cette courbe s’identifie au nœud torique $N(p,q)$.

Nœud torique $N(3,5)$.

Le nœud (courbe violette) s’enroule 3 fois autour d’un tore dans une direction pendant qu’il s’enroule 5 fois dans l’autre direction.

Pour des raisons évidentes de symétrie, $\Sigma(p,q,r)$ est aussi un revêtement de degré $p$ au dessus du noeud $N(q,r)$ et une revêtement d’ordre $q$ sur le nœud $N(p,r)$.

Il est expliqué ici que la sphère de Brieskorn $\Sigma(5,3,2)$ n’est autre que la sphère d’homologie de Poincaré. On obtient donc une nouvelle construction de la sphère d’homologie de Poincaré : comme revêtement ramifié sur un nœud torique.

On trouvera ici une vidéo illustrant le fait que la sphère d’homologie de Poincaré est un revêtement ramifié de degré 5 sur le noeud de trèfle. La méthode employée dans cette vidéo ne passe pas par les sphères de Brieskorn : elle utilise les diagrammes de Heegaard et les glissements d’anses.

Les espaces lenticulaires

Nous allons voir que les espaces lenticulaires sont des revêtements doubles ramifiés au dessus d’entrelacs à deux ponts.

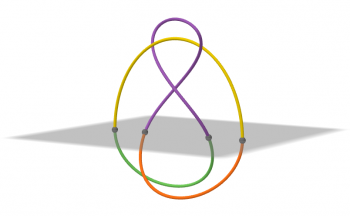
Le plan gris découpe le noeud de huit en deux arcs jaune et violet d’un côté et deux arcs orange et vert de l’autre.

Par exemple, le nœud de huit est un entrelac à deux ponts, comme illustré dans la figure ci-dessous.

Puisque le premier groupe d’homologie de la sphère $\mathbb{S}^3$ est trivial, il existe un unique revêtement double de $\mathbb{S}^3$ ramifié au dessus d’un entrelac donné. Nous allons montrer le résultat suivant :

Démonstration.
On commence par remarquer que le revêtement double d’une boule de dimension $3$ ramifié au dessus de deux arcs disjoints est un tore solide. Pour cela, réalisons le tore solide comme l’ensemble

$$\mathrm{TS}^3 = \left\{ \left(\sin(t)(1+ r \cos(u)), \cos(t)(1+ r \cos(u)), r\sin(u)\right) \mid (t,u,r) \in \mathbb{R}/2\pi \mathbb{Z} \times \mathbb{R}/2 \pi \mathbb{Z} \times [0,1/2]\right \} ~.$$

Notons $\sigma$ l’involution linéaire

$$(x,y,z) \mapsto (-x,y,-z)~.$$

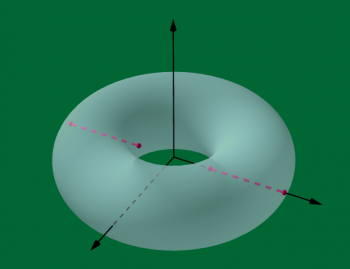
Involution du tore solide

On observe que $\sigma$ préserve le tore solide, que le quotient $\mathrm{TS}^3/\sigma$ est homéomorphe à une boule, et que la projection de $\mathrm{TS}^3$ sur $\mathrm{TS}^3/\sigma$ est un revêtement double ramifié au dessus de l’intersection du tore solide avec l’axe $x = z = 0$, dont l’image au quotient forme bien deux arcs disjoints.

Considérons maintenant un revêtement double $\pi: M \to \mathbb{S}^3$ ramifié au dessus d’un entrelac à deux ponts. Fixons un découpage de $\mathbb{S}^3$ en deux boules $U_1$ et $U_2$ d’intérieurs disjoints telles que l’intersection de notre entrelac avec chacune des boules est formée de deux arcs plongés disjoints.

Alors, d’après ce qui précède, $\pi^{-1}(U_1)$ et $\pi^{-1}(U_2)$ sont deux tores solides d’intérieurs disjoint, qui forment donc un scindement de Heegard de genre $1$ de $M$.

C.Q.F.D.

Le théorème précédent admet une réciproque :

Démonstration.

Comme les automorphismes du tore sont isotopes à des automorphismes linéaires, on peut supposer que $M$ est obtenu par recollement de deux tores solides $\mathrm{TS}_1$ et $\mathrm{TS}_2$ par un automorphisme linéaire du tore $\mathbb{R}^2 / \mathbb{Z}^2 \simeq \partial \mathrm{TS}_1 \simeq \partial \mathrm{TS}_2$. Cet automorphisme commute avec l’involution hyper-elliptique du tore qui, comme nous venons de le remarquer, se prolonge en une involution du tore solide.

Soient donc $\sigma_1$ et $\sigma_2$ deux involutions de $\mathrm{TS}_1$ et $\mathrm{TS}_2$ qui coïncident au bord avec l’involution hyper-elliptique. Alors $\sigma_1$ et $\sigma_2$ induisent une involution $\sigma$ de $M$. Le quotient de $M$ par $\sigma$ est obtenu par recollement des quotients $B_1 = \mathrm{TS}_1/\sigma_1$ et $B_2 = \mathrm{TS}_2/\sigma_2$, qui sont des boules. Par conséquent, $M/\sigma$ est homéomorphe à une sphère. Enfin, par construction, la projection de $M$ sur $M/\sigma$ est un revêtement double ramifié au dessus d’un entrelac dont l’intersection avec $B_1$ et $B_2$ est formée de deux arcs disjoints. C’est donc un entrelac à deux ponts.

C.Q.F.D.

On peut démontrer (mais c’est bien plus compliqué) que deux entrelacs à deux ponts sont isomorphes si et seulement si leur revêtements doubles sont homéomorphes.

Pour aller plus loin

Il est possible de construire d’autres variétés comme des revêtements ramifiés de la sphère $\mathbb{S}^3$ sur des entrelacs. En fait Alexander a montré qu’on pouvait obtenir ainsi toutes les variétés compactes [1].