La variété dodécaédrique de Poincaré comme revêtement de l’hypersphère ramifié au-dessus du noeud de trèfle

« »
On définit ici la variété dodécaédrique de Poincaré $\Sigma$ en identifiant par paires les faces opposées d’un dodécaèdre via une translation suivie d’une rotation d’un dixième de tour. La relation d’équivalence engendrée par ces identifications est compatible avec l’action du groupe alterné $A_5$ des symétries directes du dodécaèdre : si deux points du dodécaèdre sont identifiés, alors leurs images par une symétrie directe du dodécaèdre seront aussi identifiées. Le groupe des symétries directes du dodécaèdre opère donc fidèlement, par difféomorphismes [1], sur $\Sigma$.

Considérons l’action cyclique sur $\Sigma$ induite par une des rotations d’ordre 5 du dodécaèdre et notons $\overline{\Sigma}$ l’espace quotient.

Le but de cet article est de démontrer en images le théorème suivant.

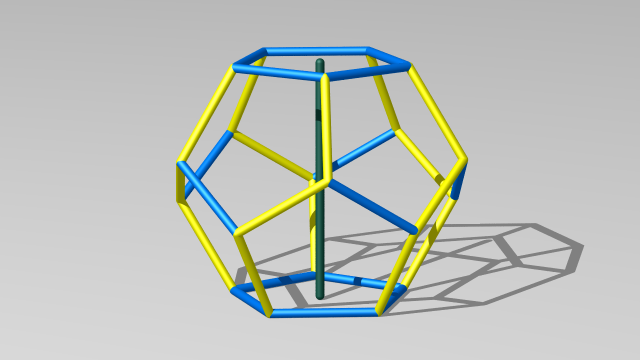
Démonstration. Considérons une rotation d’ordre 5 du dodécaèdre régulier, et notons $\varphi$ le difféomorphisme induit par cette rotation sur $\Sigma$. L’axe de la rotation considérée passe par les centres de deux faces opposées du dodécaèdre, que nous noterons $A$ et $A'$. Dans les vidéos ci-dessous, l’axe de la rotation est représenté vertical, et les faces $A$ et $A'$ sont donc horizontales. Chaque couleur désigne une classe d’arêtes pour la relation d’équivalence induite par les identifications de faces définissant $\Sigma$.

Plutôt que de quotienter $\Sigma$ par $\varphi$, on peut d’abord quotienter le dodécaèdre par la rotation d’ordre 5 puis ensuite recoller les faces du quotient par l’identification induite. Pour cela, avant de procéder à la construction de $\overline{\Sigma}$ à proprement parler, commençons par expliciter l’action de la rotation d’ordre 5 sur les paires de faces et sur les triplets d’arêtes identifiées dans $\Sigma$ (voir ici [2]).

Il y a deux orbites de paires de faces opposées. La première orbite est constituée d’une seule paire de faces : la paire $\{ A , A' \}$. L’autre orbite est constituée des cinq autres paires de faces (qui sont permutées cycliquement par notre rotation d’ordre 5).

Les arêtes du dodécaèdre sont identifiées trois par trois dans $\Sigma$. On s’intéresse à l’action de la rotation d’ordre 5 sur ces triplets d’arêtes du dodécaèdre. Il y a deux orbites de triplets d’arêtes. L’une des orbites est constituée des arêtes qui au départ sont jaunes, rouges, oranges, dorées, mauves ; au cours de la vidéo, ces arêtes sont peu à peu coloriées en jaune. L’autre correspond aux arêtes bleu clair, vert foncé, blanches, vert clair, et bleu foncé ; au cours de la vidéo, ces arêtes sont peu à peu coloriées en bleu clair. Dans $\overline{\Sigma}$, chacune de ces deux couleurs correspondra à une unique 1-cellule.

A l’issue de cette étude, lançons-nous dans la construction de $\overline{\Sigma}$ à proprement parler.

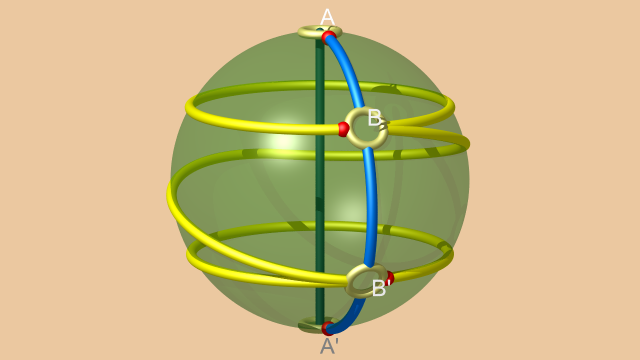
Comme annoncé, on commence par quotienter le dodécaèdre (plein) par la rotation d’ordre 5. Topologiquement, le quotient est encore une boule. Cependant, dans la boule quotient il y a un segment de points spéciaux qui sont les images des points fixes de la rotation, autrement dit son axe. Pour visualiser ce quotient on peut découper le dodécaèdre en 5 « tranches » puis recoller l’une de ces tranches le long des coupures, comme dans la vidéo suivante. On y représente également la décomposition cellulaire du bord de la boule quotient induite par la décomposition polyédrale du bord du dodécaèdre.

En effet, la cellulation du (bord du) dodécaèdre induit une cellulation du bord de la boule quotient contenant deux paires de faces : une première paire est constituée des images des faces $A$ et $A'$ (les calottes sphériques bordées par les « cercles polaires » bleus sur l’image ci-dessous), tandis que la deuxième paire, que l’on notera $\{B , B'\}$ et qui correspond aux autres faces du dodécaèdre, est constituée de deux pentagones dont l’intérieur est plongé mais pas le bord (dont deux arêtes sont identifiées, le long d’une arête jaune sur l’image ci-dessous). On a pris soin de conserver la coloration jaune ou bleue des 1-cellules de la cellulation induite, selon qu’elles proviennent de la première ou de la seconde orbite de triplets d’arêtes.

Les identifications qui définissent la variété dodécaédrique (des vissages d’un dixième de tour) induisent des identifications sur le bord de la nouvelle boule. Et l’espace quotient $\overline{\Sigma}$ est le quotient de cette nouvelle boule par ces identifications. La coloration des 1-cellules ne laisse aucune ambiguïté sur les identifications en question (vissage d’un demi tour entre les « calottes polaires », si on imagine celles-ci plates, et quelque chose d’un peu plus compliqué pour les faces pentagonales immergées, que nous laissons en exercice au lecteur, en sachant que nous ne nous en servirons pas dans la suite).

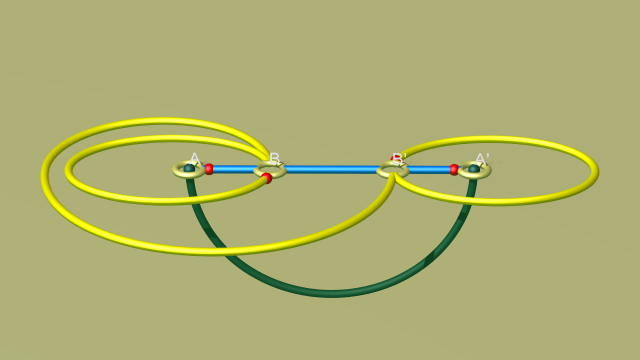
Tout comme pour une variété polyédrique, cette construction par identifications de faces par paires munit $\overline{\Sigma}$ d’une décomposition en anses particulière (qui n’est autre que le quotient par $\varphi$ de la décomposition en anses de la variété polyédrique $\Sigma$, celle-ci étant préservée par $\varphi$). Cette décomposition est codée par un diagramme de Heegaard indiquant comment recoller au bord d’une 0-anse (l’intérieur de la boule verte ci-dessus) deux 1-anses (une par paire de faces) et deux 2-anses (dont le mode d’attachement est codé par les courbes bleue et la jaune). Ici encore, ce diagramme est « dual » à la cellulation du bord de la boule quotient. On représente ce diagramme « dual » dans l’animation suivante. On le pense dessiné sur le bord de la 0-anse, dans laquelle on continue de représenter l’ensemble des points fixes de $\varphi$ qui à l’issue des attachements d’anses constituera le lieu de branchement de la projection $\Sigma \to \varphi \backslash \Sigma$. À partir de ce diagramme, il s’agira ensuite de vérifier que la variété finale est une 3-sphère, et que l’image dans cette hypersphère de la courbe vert foncé est un nœud de trèfle.

Voici-donc la 0-anse et le diagramme de Heegaard sur son bord.

On pense pour l’instant cette 0-anse comme plongée dans $\mathbb{S}^3$, qui nous apparaît à l’écran comme $\mathbb{R}^3$ à la suite d’une projection stéréographique. Dans l’animation suivante, on déplace le pôle de cette projection jusqu’au bord de la 0-anse.

Le bord de la 0-anse et le diagramme de Heegaard qu’il porte deviennent donc planaires (le diagramme est la seule trace visible de ce plan sur toutes les images qui suivent).

On peut maintenant chercher à identifier le quotient $\overline{\Sigma}=\varphi \backslash \Sigma$ à l’aide d’opérations élémentaires sur le diagramme de Heegaard. Mais nous voulons également connaître la forme de la courbe verte à l’issue des recollements d’anses. On distingue alors deux types d’opérations élémentaires : celles où l’on se contente de bouger, par isotopie, les courbes jaune et bleue et celles où l’on bouge les anses, autrement dit les cercles beiges. Les opérations du premier type n’affectent pas la classe d’isotopie de l’image de la courbe verte dans la variété $\overline{\Sigma}$. [3] Il faudra par contre prendre garde à la manière dont les opérations du deuxième type affectent le plongement de la courbe verte dans la 0-anse.

On commence par simplifier la courbe bleue pour amener la 2-anse correspondante en position d’élimination avec la 1-anse $AA'$. Pour cela, on effectue deux glissements d’anses. Rappelons que cela consiste à recoller à la 0-anse les deux 1-anses $AA'$ et $BB'$ puis à déformer le corps en anses ainsi obtenu (et bien entendu les courbes fermées bleues et jaunes tracées sur son bord) en faisant glisser le pied de l’une des anses sur la surface de l’autre anse, le diagramme obtenu en retirant à la fin les deux 1-anses définissant naturellement la même variété que le diagramme initial. Cette opération bouge les cercles beiges, c’est donc une opération du deuxième type et il nous faut suivre ce qu’il advient de la courbe verte lors de cette déformation, pour comprendre ce qu’elle sera dans la variété finale $\overline{\Sigma}$.

Rappelons donc tout d’abord que l’attachement des 1-anses équivaut à identifier les disques $A$ et $A'$ et $B$ et $B'$, et en particulier les extrémités de la courbe verte. Dans le corps en anse ainsi obtenu, cette dernière est une courbe fermée constituée de deux arcs, l’un reliant les centres des disques $A$ et $A'$ dans la 0-anse, l’autre dans la 1-anse. Le pied de l’anse qui « glisse » entraîne donc avec lui, avec les courbes bleues et jaunes, la courbe verte en surface de la 0-anse d’abord, puis sur le bord de l’anse qu’il escalade, puis dans le bord de la 0-anse à nouveau, etc...

On aboutit après les glissements au diagramme suivant sur le bord de la 0-anse :

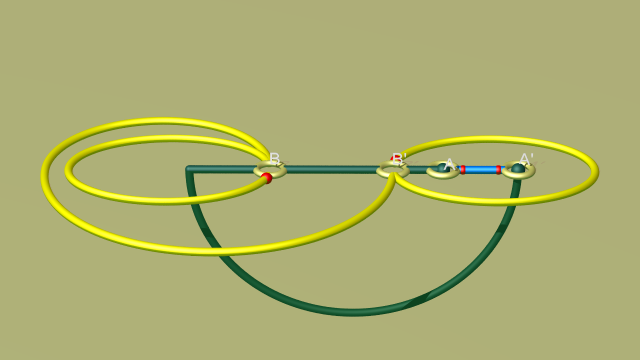
Dans ce diagramme on prendra bien garde à distinguer les courbes jaune et bleue — qui servent à montrer où recoller les 2-anses — de la courbe verte qui représente elle l’axe des points fixes de $\varphi$. Une partie de cet axe se trouve sur le bord de la 0-anse, une autre dans son intérieur. [4] Si l’on ajoute les 1-anses, ces arcs verts se referment en une courbe fermée simple comprenant en outre un arc parcourant l’intérieur de l’anse $AA'$ et deux arcs sur le bord de l’anse $BB'$ (cf. l’article diagrammes de Heegaard).

Après élimination des anses complémentaires correspondant à la 1-anse $AA'$ on aboutit au plan de construction suivant où pour une fois, pour simplifier l’étape suivante, on a choisi de spécifier comment se recollent chaque paire d’extrémités de brins jaunes plutôt qu’une seule :

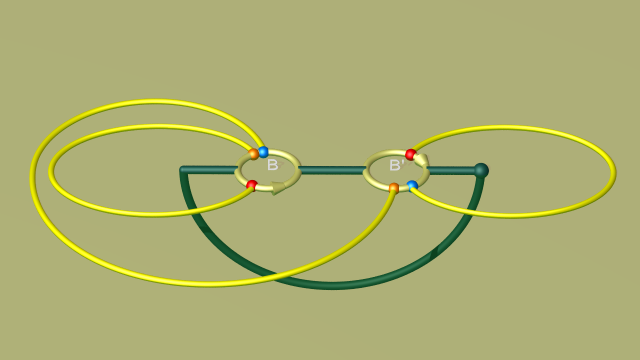
L’élimination des deux anses complémentaires a eu pour effet d’identifier sur le bord de la nouvelle 0-anse les extrémités de l’axe vert des points fixes qui occupaient les centres des faces $A$ et $A'$. Dans le corps en anses obtenu en ajoutant l’anse $BB'$, cet axe est maintenant une courbe fermée simple qui part disons de ce point d’identification (représenté par une petite boule verte), rejoint son point antipodal par l’intérieur de la 0-anse, rejoint le bord du disque d’attachement $B'$, parcourt une première fois l’anse $BB'$ (sur son bord), joint le pied $B'$ au pied $B$ par le bord de la $0$-anse, puis grimpe à nouveau sur l’anse $BB'$, pour enfin rejoindre son point de départ par le bord de la 0-anse. [5]

Il s’agit encore de montrer que le diagramme de genre 1 ci-dessus code une décomposition en anses de l’hypersphère $\mathbb{S}^3$ puis de montrer que l’image de la courbe verte dans ce $\mathbb{S}^3$ est isotope au noeud de trèfle. Commençons par remarquer que la courbe jaune présente une boucle superflue. L’opération qui consiste à simplifier cette boucle superflue est une opération du premier type, on peut donc oublier la courbe verte. On aboutit au diagramme suivant :

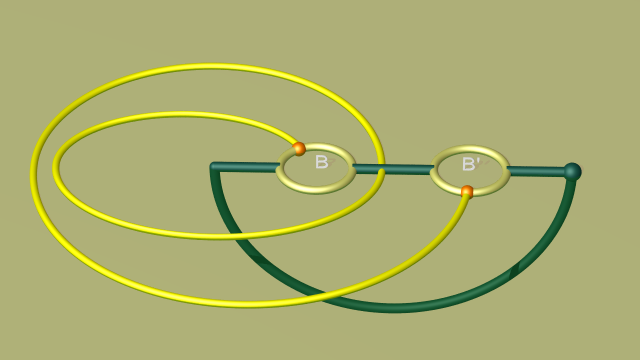
Pour plus de clarté dans les animations suivantes, on pousse maintenant légèrement l’arc central de la courbe verte à l’intérieur de la 0-anse (ce qui ne change évidemment ni la variété finale ni la classe d’isotopie de la courbe verte dans cette variété). On aboutit au diagramme suivant (dans lequel on n’affiche plus la marque orange puisque la courbe jaune a un seul pied sur chaque disque) :

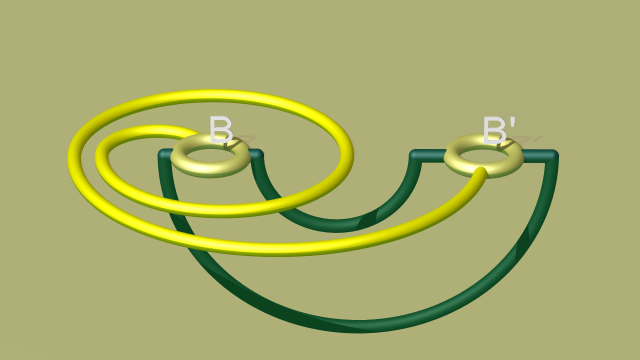
Une isotopie de la 0-anse tout entière (qui n’affecte donc ni la variété finale ni la classe d’isotopie de la courbe verte dans cette variété) permet de simplifier ce diagramme en faisant glisser le disque $B'$ autour du disque $B$ en suivant la boucle jaune. Cette isotopie, qui est une opération du deuxième type, « complique » la partie de la courbe verte contenue dans l’intérieur de la 0-anse comme le montre la vidéo suivante.

On aboutit au diagramme suivant pour lequel la 2-anse qui correspond à la courbe jaune est maintenant en position d’élimination avec la 1-anse $BB'$ :

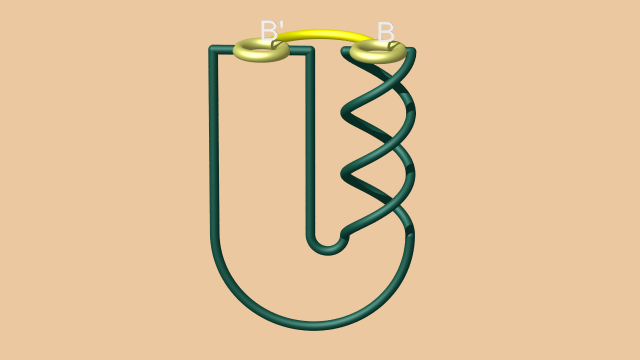
L’ajout à la 0-anse (le demi-espace inférieur, dont on ne devinait le bord que grâce aux courbes du diagramme) des deux anses en position d’élimination nous laisse à nouveau avec une 0-anse dont on ne voit plus le bord dans le film qui suit, puisque le scindement de Heegaard ainsi obtenu est maintenant de genre 0, donc son diagramme vide ! L’élimination des anses complémentaires identifie en outre deux à deux les pieds de la courbe verte sur les disques $B$ et $B'$ pour donner un nœud, comme le montre le film suivant.

On peut penser le bord de la nouvelle 0-anse comme le plan horizontal contenant les deux brins horizontaux supérieurs du nœud ainsi obtenu, on encore penser que ce que l’on voit sur l’image finale ci-après est $\overline{\Sigma}$ privé d’une 3-anse (ou plus simplement d’un point).

Le noeud obtenu est le noeud de trèfle :

Et en recollant la dernière 3-anse au bord de la 0-anse on obtient le résultat annoncé : la variété dodécaédrique de Poincaré est le revêtement de $\mathbb{S}^3$ de degré 5 ramifié au-dessus du noeud de trèfle. [6]

C.Q.F.D.

$$ $$

En utilisant la description des sphères d’homologie de Brieskorn on a le

Ce corollaire et les généralités sur les sphères de Brieskorn permettent de conclure que $\Sigma$ est aussi le revêtement de degré 3 du noeud torique $T(2,5)$ et le revêtement double du noeud torique $T(3,5)$, ce que l’on pourrait retrouver en procédant comme dans la démonstration du théorème ci-dessus.