Un diagramme de Heegaard de genre $2$ de la variété dodécaédrique de Poincaré

On montre ici que la variété dodécaédrique de Poincaré définie en identifiant par paires les faces opposées d’un dodécaèdre via une translation suivie d’une rotation d’un dixième de tour possède un scindement de Heegaard de genre 2.

Pour cela, on part du diagramme de Heegaard qui lui est naturellement associé en tant que variété polyédrique [1], et on fait subir à celui-ci une suite de manipulations élémentaires qui ne changent pas la topologie de la variété associée et qui aboutissent à un diagramme de genre 2.

Ce dernier n’est pas le diagramme donné par Poincaré dans le cinquième complément, mais nous démontrons dans un autre article l’équivalence entre ces deux diagrammes de genre 2. En d’autres termes, la sphère d’homologie que construit Poincaré dans le cinquième complément et la variété dodécaédrique (construite à partir du dodécaèdre) sont une seule et même variété.

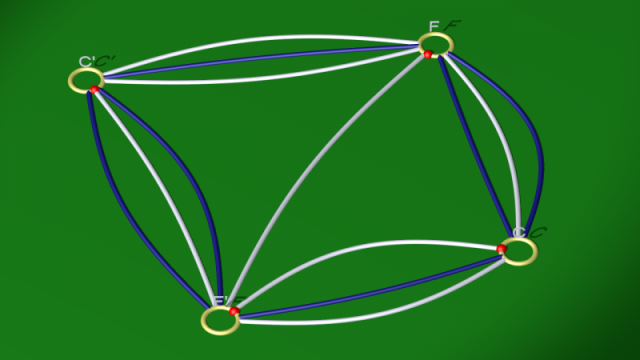
On part donc du diagramme (sphérique) de genre 6 de la variété dodécaédrique. Les disques d’attachement des 1-anses ont été symboliquement représentés ici par des demi-sphères plus foncées. Chaque 1-anse relie deux disques diamétralement opposés.

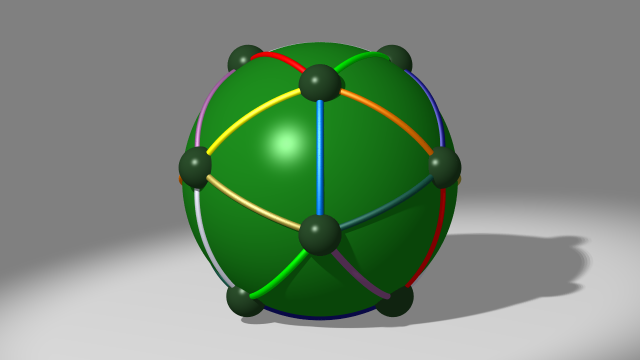
Dans la vidéo qui suit, on commence par mettre ce diagramme sous forme planaire, et on rappelle, dans cette configuration, où doivent être attachées les 1-anses [2]. Chaque couleur rencontrant au plus une fois un disque d’attachement, il n’y a ici aucune ambiguïté sur la façon dont deux tels disques sont identifiés lors de l’attachement d’une 1-anse. Il n’est donc pas nécessaire de spécifier cette identification par un point marqué comme nous l’avions fait là.

Remarque. Ici et dans les films qui suivent, le prolongement dans les 1-anses des courbes colorées de recollement des 2-anses est représenté de façon symbolique : ces courbes devraient être en surface des anses, et se recoller précisément aux courbes planaires de la même couleur, et pour cela éventuellement « tourner » autour des anses comme dans cet article. En outre, on ne représentera pas toujours l’intégralité des courbes traversant une anse donnée mais, parfois, seulement celle de la couleur qui nous importe à un moment donné. Le diagramme planaire en revanche, sera complet.

1. La première étape consiste à simplifier la courbe vert foncé pour amener la 2-anse correspondante en position d’élimination avec la 1-anse $AA'$. Pour cela, on effectue deux glissements d’anses.

$$ $$

On aboutit après les glissements au diagramme suivant (à ce stade, il devient préférable, même si pas encore indispensable, de spécifier l’identification des disques d’attachement à l’aide de marques rouges).

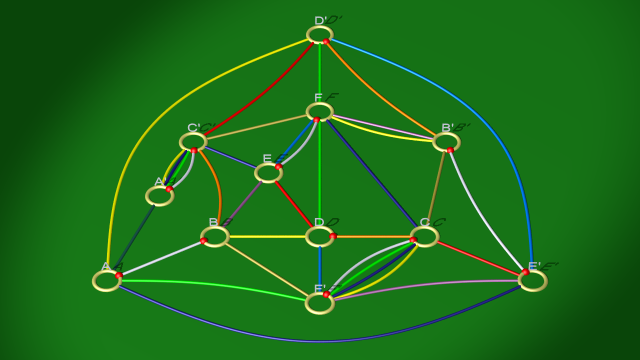
Après élimination des anses complémentaires ce diagramme devient :

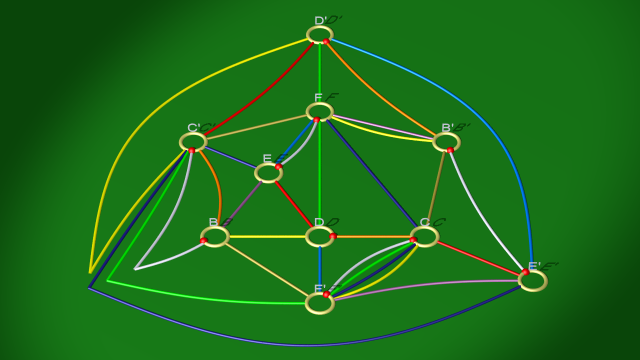
Diagramme qui est lui-même isotope au diagramme suivant.

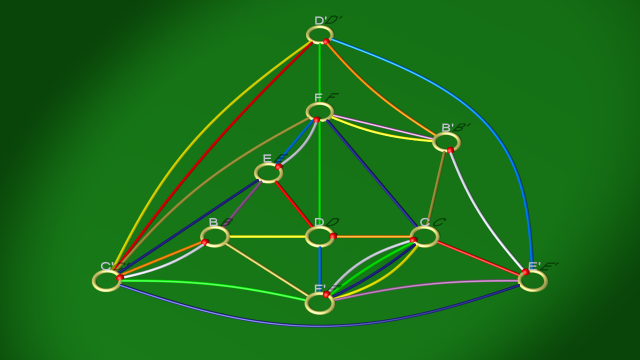
2. De la même façon, on simplifie la courbe rouge à l’aide de deux glissements d’anses, ce qui l’amène en position d’élimination avec la $1$-anse $DD'$.

$$ $$

Voici les diagrammes après glissement, avant et après élimination des anses complémentaires :

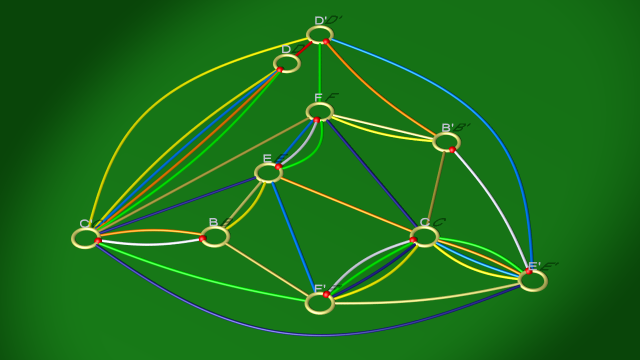
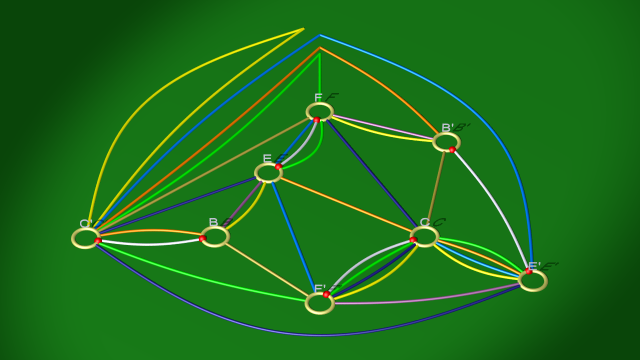
le second étant à son tour isotope à :

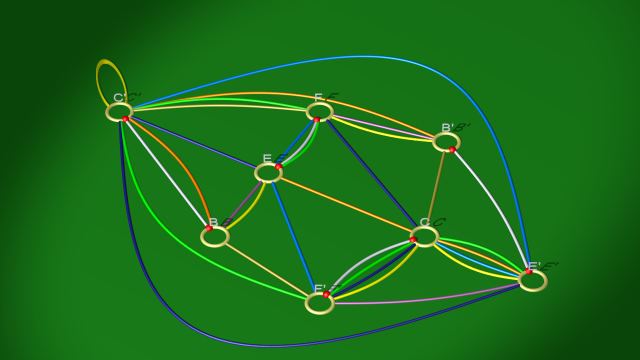
3. On aboutit à un diagramme de genre 4. La courbe jaune présente une boucle superflue, que l’on peut simplifier.

$$ $$

On aboutit au diagramme suivant :

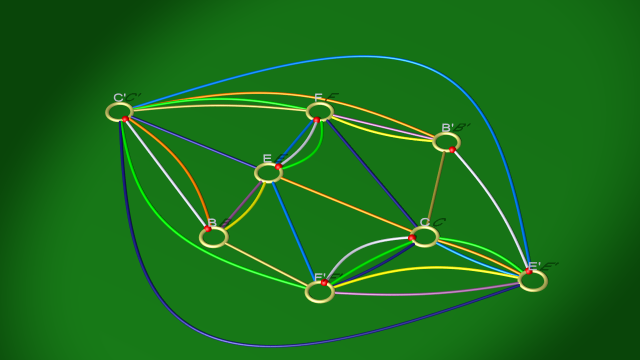
4. On simplifie ensuite la courbe mauve à l’aide de deux glissements d’anses et on l’élimine avec l’anse $BB'$.

$$ $$

Voici les diagrammes après glissements, avant et après élimination des anses complémentaires :

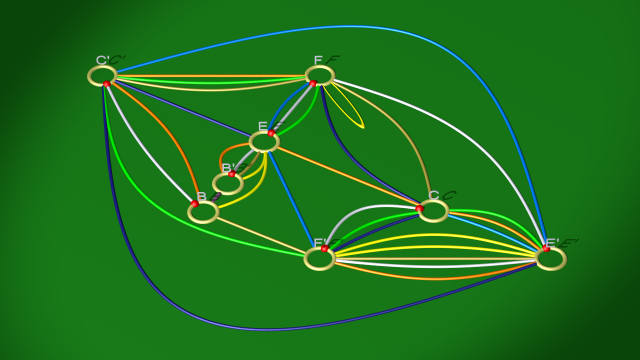
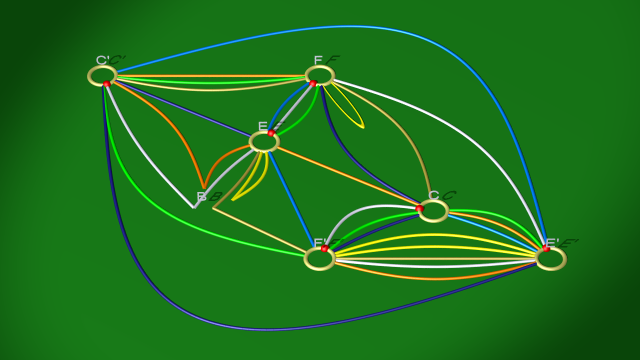
le second étant isotope à :

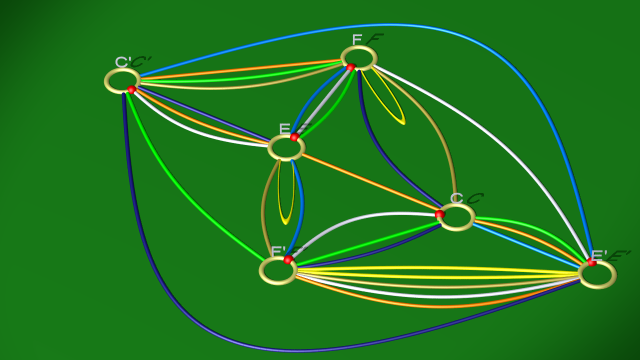
5. La courbe jaune est maintenant homotopiquement triviale dans le bord du corps en anses de genre 4 obtenu en attachant les 1-anses, comme on peut le voir sur la vidéo suivante (où on effectue deux simplifications de boucles superflues) :

$$ $$

On peut donc la supprimer (ce qui correspond à l’annulation d’une 2-anse et d’une 3-anse). On aboutit au diagramme suivant :

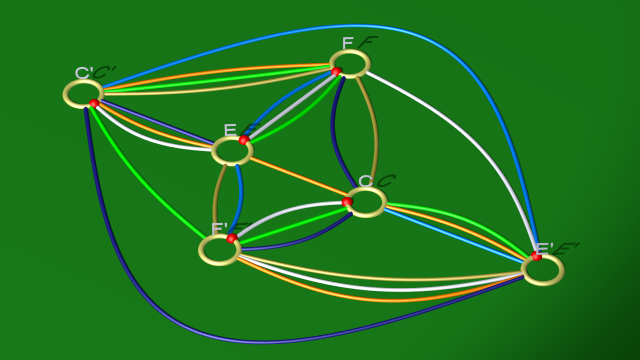
6. Trois glissements d’anses permettent alors d’éliminer la courbe dorée avec la 1-anse $EE'$.

$$ $$

Voici les diagrammes avant et après élimination :

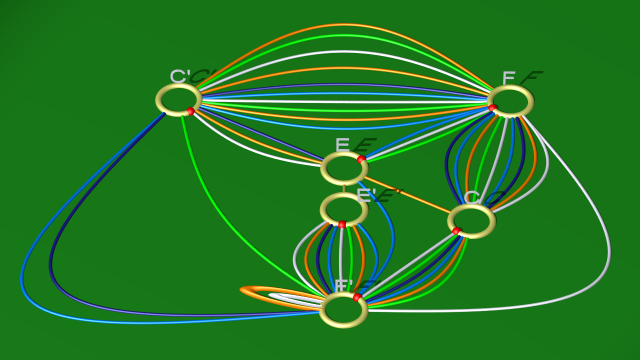
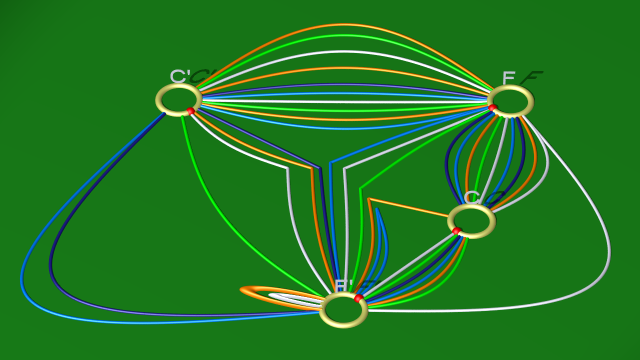
le second étant isotope à :

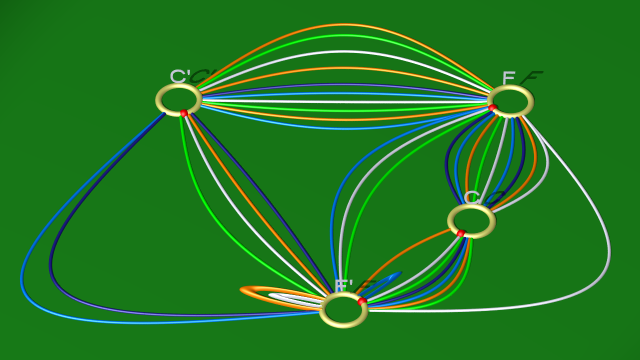
7. On se retrouve avec trois boucles blanche, orange et bleue que l’on simplifie.

$$ $$

On aboutit alors au diagramme :

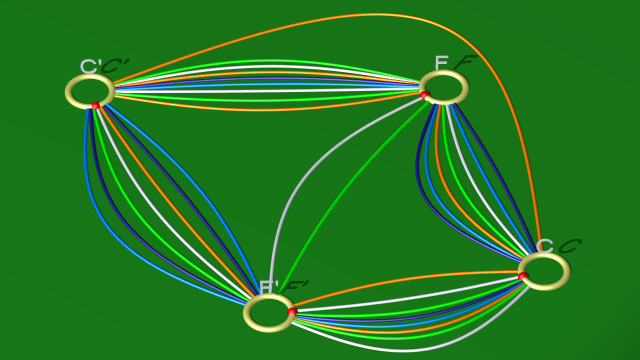
8. On constate alors que les courbes blanche et verte sont homotopes. On peut donc supprimer l’une d’elles (disons la verte) purement et simplement, ce qui revient à supprimer la 2-anse correspondante et une 3-anse de la décomposition. On supprime pour la même raison l’une des deux courbes bleues.

$$ $$

Le résultat est :

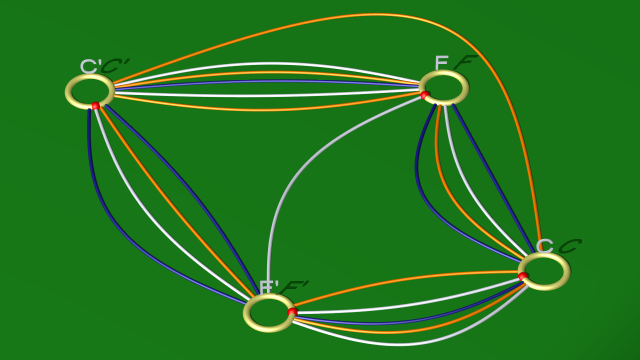
9. Maintenant, on complique dans un premier temps le diagramme pour faire apparaître la courbe bleue comme « facteur » de la courbe orange, que l’on peut alors « simplifier » par ce facteur.

$$ $$

Cette simplification consiste à passer du diagramme :

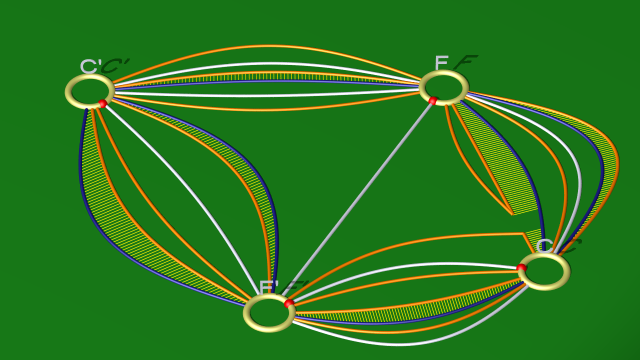
au diagramme :

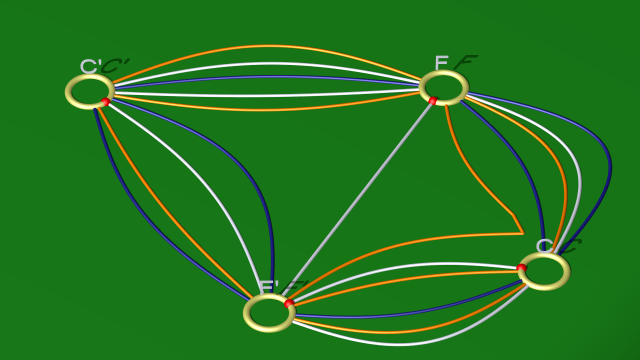
ou encore :

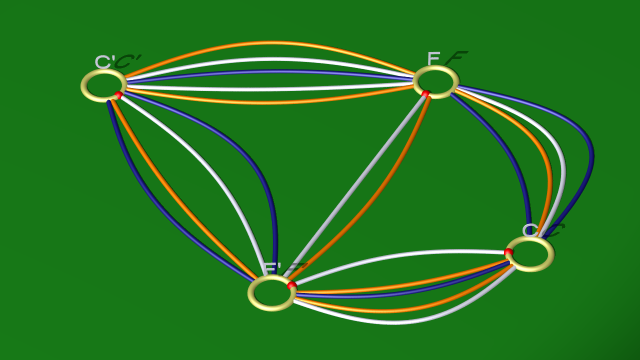
10. Les courbes blanche et orange sont alors homotopes. On peut donc éliminer la orange (i.e. la 2-anse correspondante et une 3-anse).

$$ $$

On aboutit à un (vrai) diagramme de genre 2.

En effet, on a éliminé de la décomposition quatre 1-anses ($AA'$ (cf. 1), $DD'$ (cf. 2), $BB'$ (cf. 4), $EE'$ (cf. 6)), huit $2$-anses (vert foncé (cf. 1), rouge (cf. 2), mauve (cf. 4), jaune (cf. 5), dorée (cf. 6), verte (cf. 8), bleue claire (cf. 9), orange (cf. 11)) et quatre 3-anses (cf. 5, 8, 9, 11). Il reste donc bien une 0-anse, deux 1-anses, deux 2-anses et une 3-anse.

On montre ici que ce diagramme est équivalent à celui donné par Poincaré dans le cinquième complément.

On montre en outre là que la variété définie par ce diagramme, qui est donc la variété dodécaédrique de Poincaré, peut aussi s’obtenir par chirurgie sur le nœud de trèfle.