|
> Exemples de dimension 3 > Topologie des variétés de dimension 3 > Opérations élémentaires sur les diagrammes de Heegaard Opérations élémentaires sur les diagrammes de Heegaard |
Une variété donnée possède une infinité de scindements de Heegaard. On décrit ici plusieurs opérations élémentaires sur les diagrammes de Heegaard qui ne modifient pas la variété associée. [1]
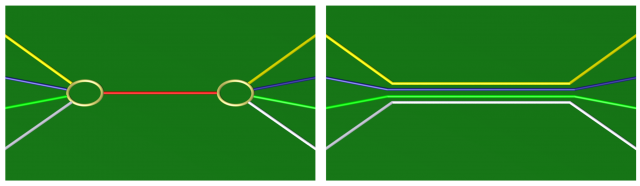
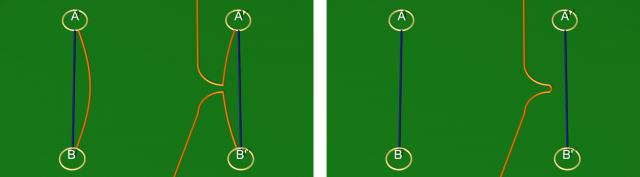
On commence par une manipulation qui permet de réduire le genre d’un diagramme, sans bien sûr changer la variété associée.
Une telle réduction est possible lorsque, dans la décomposition en anses codée par le diagramme, une 1-anse et une 2-anse se trouvent en position d’annulation. Sur le diagramme, cela correspond à la situation particulière où l’une des courbes de recollement est formée d’un arc unique, comme l’arc rouge de la première figure ci-dessus (qui relie nécessairement deux disques d’attachement d’une même 1-anse).
En effet, dans cette situation, pour construire une variété par attachements d’anses à partir du plan de construction qu’est le diagramme, on peut commencer par attacher à une 0-anse (dont le bord privé d’un point est identifié au diagramme) une 1-anse entre les deux disques en question — ce qui revient à les identifier, ainsi que les extrémités de l’arc rouge considéré — puis une 2-anse le long de la courbe fermée rouge ainsi obtenue.
Or, comme le montre la vidéo ci-dessus, attacher ces deux anses revient à faire une somme connexe avec une boule, opération « neutre » qui nous laisse à nouveau avec une 0-anse. La variété finale (obtenue après attachement de toutes les anses restantes) possède donc en fait une décomposition en anses avec une 1-anse et une 2-anse de moins, i.e. un scindement de Heegaard de genre un de moins.
Quant aux éventuelles autres courbes d’attachement qui passaient par la 1-anse « éliminée », leur portion qui se trouvait dans le bord de ladite anse se trouve maintenant dans le bord de la nouvelle 0-anse. Autrement dit, sur le nouveau diagramme, les disques et courbes d’attachement des deux anses à éliminer sont remplacés par les arcs reliant deux à deux les extrémités des arcs d’attachement aboutissant à ces disques, comme sur la deuxième figure ci-dessus.
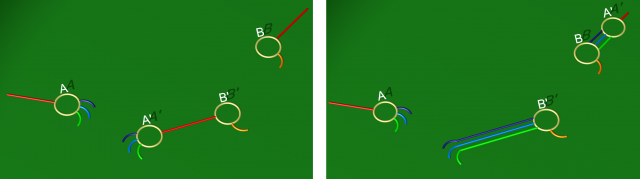
En général, une courbe d’attachement est composée de plusieurs arcs de même couleur. Pour se ramener à une situation d’élimination comme celle du paragraphe précédent, il s’agit donc de diminuer le nombre d’arcs d’une couleur donnée. Cela est parfois possible grâce à un glissement d’anse, comme nous allons l’illustrer sur un exemple.
On part du premier diagramme ci-dessus, et on souhaite réduire d’un le nombre d’arcs de la courbe d’attachement rouge.
Une fois encore, on voit le diagramme comme le bord d’une 0-anse dans $\mathbb{S}^3$, et on commence par construire (dans $\mathbb{S}^3$ toujours), un corps en anses en attachant des 1-anses aux emplacements prévus. [2] La variété finale codée par le diagramme s’obtient en attachant des 2-anses au bord de ce corps en anses, puis des 3-anses à la variété à bord ainsi obtenue.
Déformer au préalable le corps en anses par isotopie dans $\mathbb{S}^3$ n’affecte donc pas la variété finale. La vidéo ci-dessus présente une telle isotopie, qui consiste à faire « glisser » l’un des deux pieds de 1-anses reliés par l’arc rouge qu’on veut éliminer le long de cet arc, puis de la portion de l’arc rouge empruntant la deuxième anse. Avec le « pied glissant » sont entraînées toutes les autres courbes d’attachement y aboutissant. Ainsi, à l’issue de l’isotopie, la courbe rouge n’emprunte plus la deuxième anse, mais y est remplacée par toute la famille des courbes colorées entraînées par l’isotopie.
Si l’on retire les 1-anses, on obtient donc le diagramme de droite ci-dessus.
Notons que cette manipulation ne simplifie effectivement la courbe rouge que si celle-ci ne passait qu’une fois dans la première 1-anse. Dans le cas contraire, l’arc éliminé est remplacé par de nouveaux arcs rouges.
De manière générale, si cette manipulation est une simplification au sens où elle diminue en principe le nombre d’arcs d’une couleur donnée, elle complexifie également le diagramme en lui ajoutant de nombreux arcs d’autres couleurs !
$$ $$
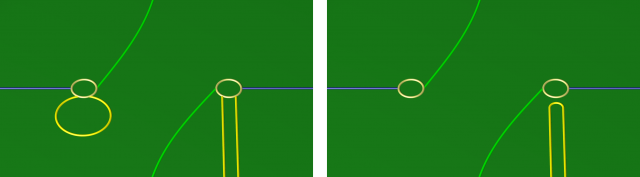
À l’issue d’une des manipulations ci-dessus, il se peut qu’un fragment de courbe d’attachement (jaune sur la figure de gauche ci-dessus) ait ses deux extrémités sur un même disque d’attachement. Comme le montre la vidéo suivante, cela signifie, lorsqu’on attache la 1-anse correspondante, que la courbe d’attachement jaune emprunte l’anse dans un sens puis fait demi-tour et l’emprunte dans l’autre sens. Mais alors on peut, par isotopie, retirer cet aller-retour superflu, si bien que la courbe jaune (ou du moins cette portion) ne passe plus dans l’anse. On aboutit alors au diagramme de droite ci-dessus.
$$ $$
Les deux situations que nous décrivons dans la suite ne peuvent se produire que si l’on est parti d’un diagramme de Heegaard généralisé. Pour un vrai diagramme de Heegaard, les courbes d’attachement sur le bord du corps en anse forment une famille libre en homologie. Ce n’est en général pas le cas pour un diagramme de Heegaard généralisé, où ces courbes peuvent être en nombre supérieur au genre du corps en anse.
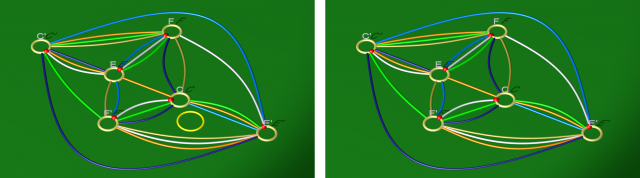
Considérons d’abord le cas où l’une des courbes est homotopiquement triviale. On montre que dans ce cas, on peut purement et simplement retirer cette courbe du diagramme, sans effet sur la variété produite.
En effet, comme le montre le film ci-dessus, attacher au corps en anse une 2-anse le long de cette courbe d’attachement revient topologiquement à lui retirer une boule, mais ce trou sera in fine rebouché par l’attachement d’une 3-anse ! Autrement dit, l’attachement successif de cette 2-anse et de cette 3-anse constitue une opération triviale. Et retirer cette étape triviale du plan de construction revient précisément à retirer la courbe jaune du diagramme de Heegaard.
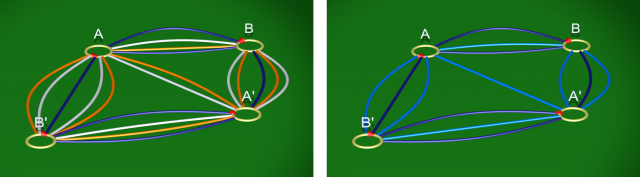
Considérons maintenant le cas où deux courbes d’attachement sont homotopes. Pour cela, il suffit que les arcs correspondants dans le diagramme soient homotopes relativement aux pieds des 1-anses, comme sur la figure en bas à gauche ci-dessus. Dans ce cas, on peut supprimer purement et simplement l’une des deux courbes, sans effet sur la variété produite.
En effet, comme le montre le film ci-dessus, l’attachement de deux 2-anses à un voisinage annulaire des courbes jumelles dans le corps en anses, laisse à l’intérieur du tube un espace homéomorphe à une boule. Cet espace est in fine occupé par une 3-anse. Il revient donc au même de fusionner les deux courbes homotopes et de recoller à la courbe obtenue une 2-anse.
Remarquons que, bien que l’effet sur le diagramme soit sensiblement différent, la simplification de deux courbes homotopes est une opération similaire à l’élimination d’une courbe homotopiquement triviale. En effet, après attachement d’une 2-anse le long d’une des courbes jumelles, la seconde devient homotopiquement triviale dans le bord de la nouvelle variété à bord. Cette seconde courbe d’attachement est donc superflue comme expliqué plus haut.
On peut effectuer cette manipulation lorsque la classe d’homotopie libre définie par la courbe d’attachement $b$, comme la courbe bleue sur la figure à gauche ci-dessus, apparaît comme facteur de la classe d’homotopie libre définie par une autre courbe d’attachement $a$, comme la courbe orange sur la figure à gauche ci-dessus. Dans le groupe fondamental cela revient à demander qu’il existe une troisième classe d’homotopie libre $c$ telle que $a=bc$. [3] Plus géométriquement, cela revient à demander qu’il existe un troisième lacet $c$ tel que $a$, $b$ et $c$ bordent un pantalon dans le bord du corps en anses. Dans l’exemple ci-dessus, on peut prendre pour lacet $c$ la courbe orange sur la figure de droite. Face à une telle situation, on peut remplacer la courbe d’attachement $a$ par la courbe $c$, sans effet sur la variété produite. [4] En pratique cette manipulation a un intérêt lorsque la courbe $c$ est « plus simple ». [5]
En effet, comme le montre le film ci-dessus, après attachement d’une 2-anse le long de $b$, la courbe $a$ se retrouve homotope à la courbe $c$ dans le bord de la nouvelle variété, et attacher une 2-anse le long de $a$ ou le long de $c$ est alors équivalent. Le diagramme obtenu en remplaçant la courbe d’attachement $a$ par $c$ est donc équivalent au diagramme de départ.
[1] Un diagramme de Heegaard indique normalement la façon dont les $1$-anses doivent être recollées, ce que nous avons fait ici notamment à l’aide de marques rouges. Dans cette partie, nous avons omis les marques rouges lorsqu’il n’y avait aucune ambiguïté sur le recollement, une couleur donnée ne rencontrant un disque d’attachement qu’en un point au plus.
[2] Tout ceci pourrait être expliqué de façon abstraite, sans plongement dans $\mathbb{S}^3$, mais il nous semble dommage de renoncer à une visualisation concrète lorsque celle-ci s’avère possible.
[3] Ici on confond abusivement une courbe et sa classe d’homotopie libre.
[4] D’où le nom de la manipulation : on remplace les générateurs $a$ et $b$ par $b$ et $c$.
[5] Pour passer d’un diagramme de Heegaard à un autre décrivant le même espace, il peut toutefois s’avérer nécessaire de d’abord compliquer le diagramme, comme ici. On est confronté à un phénomène analogue lorsque l’on cherche par exemple à montrer qu’un groupe donné par générateurs et relations est en fait trivial.