Le théorème du domaine fondamental

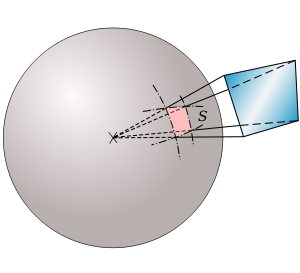
Considérons un polyèdre $P \subset \mathbb{R}^d$ avec un nombre pair de faces identifiées par paires $(F_i^-,F_i^+)$, $i=1, \ldots , m$, comme ici. Notons $\sim$ la relation d’équivalence engendrée par ces identifications de faces.

Bien que dans la construction d’une variété polyédrique on parte d’un polyèdre $P$ contenu dans un espace euclidien, on n’exige pas a priori que les identifications de faces soient réalisées par des isométries de l’espace ambiant mais seulement par des homéomorphismes PL. La seule structure naturellement portée par l’espace quotient $[P]:=P/\sim$ est sa structure d’espace topologique. A contrario on supposera, dans cet article, que l’on peut réaliser le polyèdre $P$ dans un espace $X$ euclidien, sphérique ou hyperbolique, et, surtout, que l’on peut réaliser les identifications de faces par des isométries directes de l’espace $X$. L’objet du théorème du domaine fondamental est alors de donner une condition suffisante pour que l’espace quotient $[P]$ s’identifie au quotient de $X$ par un sous-groupe discret d’isométries.

Dans la suite, on fixe un entier $n \geq2$, on note $X$ l’espace euclidien $\mathbb{R}^n$, la sphère $\mathbb{S}^n$ ou l’espace hyperbolique $\mathbb{H}^n$, et $G$ le groupe des isométries directes de $X$.

$G$-appariement d’un polyèdre dans $X$

On dispose dans $X$ d’une notion naturelle d’hyperplan : les hyperplans affines dans $\mathbb{R}^n$, les grandes sphères dans $\mathbb{S}^n$ et les sous-espaces hyperboliques de codimension 1 dans $\mathbb{H}^n$. Un hyperplan dans $X$ borde deux demi-espaces.

Considérons un polyèdre $P \subset X$ avec un nombre pair, égal à $2m$, de faces. On veut encore identifier toutes les faces (de codimension 1) par paires $(F_i^-,F_i^+)$, $i=1, \ldots , m$, et considérer l’espace quotient. Mais cette fois on veut réaliser ces identifications par des isométries directes de $G$. Cela motive la définition suivante.

Supposons dorénavant que $P$ est muni d’un $G$-appariement $\Phi$. Cet appariement engendre une relation d’équivalence $\sim$ sur $P$. On appelle cycle toute classe d’équivalence. L’espace quotient $[P]=P/ \sim$ est aussi l’espace des cycles. Pour tout entier $k \in \mathbb{N}$, l’appariement $\Phi$ engendre une relation d’équivalence sur l’ensemble des $k$-faces de $P$. On appelle cycle de $k$-faces une classe d’équivalence.

Le théorème du domaine fondamental

Chaque face de codimension 2 dans $P$ est l’intersection de deux faces (de codimension 1) qui forment un angle dièdre dans $P$. On appelle angle d’un cycle de faces de codimension 2 la somme des angles dièdres de toutes les faces de codimension 2 contenues dans le cycle.

Il y a deux aspects intéressants dans ce théorème. Un premier local et un second global.

L’hypothèse sur les angles implique que les secteurs angulaires autour des faces de codimension 2 se recollent pour former des disques non singuliers, voir ici pour une animation qui illustre cela. En dimension $2$, tout point de $P$ possède donc un voisinage pavé par les images de $P$ par des isométries appartenant au groupe engendré par $\Phi$. C’est une propriété locale qui n’est plus évidente dès lors que la dimension est supérieure ou égale à 3. Ainsi lorsque $n=3$ pourquoi les secteurs angulaires d’un même cycle de sommets doivent -ils se recoller en une boule non singulière ?

Une fois vérifiée la propriété locale il faut encore démontrer que le germe de pavage engendré par $P$ (pavage d’un petit voisinage de $P$) se prolonge en un pavage de tout l’espace $X$. Ce deuxième point est de nature globale. Il est déjà intéressant en dimension 2, cas étudié par Poincaré dans son mémoire sur le groupes fuchsiens. La démonstration passe par la théorie des revêtements et la notion de complétude. Nous commençons par considérer cet aspect en démontrant une version faible du théorème du domaine fondamental.

On démontre finalement le théorème général par récurrence sur la dimension à partir de la version faible du théorème. La fait qu’il suffise de considérer les angles atour des faces de codimension 2 provient de ce que parmi les sphères $\mathbb{S}^n$, $n \geq 1$, seul le cercle $\mathbb{S}^1$ n’est pas simplement connexe. On trouve déjà trace de cet aspect dans la version topologique du théorème.

$G$-appariement propre

En tout point $x$ de $P$ on appelle angle solide de $P$ en $x$ le nombre réel

$$\omega (x) = \frac{\mathrm{vol} (P \cap B(x,r))}{\mathrm{vol} \, B(x,r)}$$

où $r$ est n’importe quel réel positif strictement inférieur à la distance de $x$ à n’importe quelle face ou facette de $P$ ne contenant pas $x$.

Soit $[x]=\{ x_1 , \ldots , x_k \}$ un cycle de $\Phi$. On appelle angle solide du cycle $[x]$ le nombre réel

$$\omega [x] = \omega (x_1) + \ldots + \omega (x_k ).$$

La métrique sur $X$ induit alors une métrique non-singulière sur le quotient $[P]$. Et ce dernier devient une variété euclidienne si $X=\mathbb{R}^n$, sphérique si $X=\mathbb{S}^n$ et hyperbolique si $X=\mathbb{H}^n$. Autrement dit, $[P]$ est une variété localement modelée sur l’espace $X$ et dont les changements de cartes peuvent être réalisés par des (restrictions d’)éléments de $G$. [2]. L’espace $X$ est l’espace modèle pour cette géométrie.

Ce fait est une reformulation du résultat, peut-être plus standard, selon lequel l’espace $\mathbb{R}^n$, resp. $\mathbb{S}^n$, $\mathbb{H}^n$, est l’unique (à isométrie près) variété riemannienne complète, simplement connexe et de courbure sectionnelle constante égale à $0$, $1$ et $-1$.

Besoin d’une « autre » démonstration ?

On propose ici un point de vue alternatif reposant sur la notion de $(G,X)$-variété. Le point clé étant que le groupe $G$ opère analytiquement sur $X$ : si deux éléments $g$ et $g'$ de $G$ et coïncident sur un ouvert non vide de $X$ alors $g=g'$.

On appelle $(G,X)$-variété toute variété localement modelée sur l’espace $X$ et dont les changements de cartes peuvent être réalisés par des (restrictions d’)éléments de $G$. Et on appelle $(G,X)$-morphisme entre deux $(G,X)$-variétés un difféomorphisme local qui se lit localement dans les cartes des $(G,X)$-structures comme l’action d’un élément de $G$. [3]

Maintenant soit $V$ une $(G,X)$-variété simplement connexe. On peut « développer » $V$ dans $X$ à partir de n’importe quel point base donné $v_0 \in V$ et ainsi obtenir un $(G,X)$-morphisme $D:V \to X$ : on commence par envoyer, via une carte locale, un voisinage de $v_0$ dans $X$. On prolonge alors cette application le long de n’importe quel chemin partant de $v_0$ : soit $v$ un point de $V$. Relions $v_0$ à $v$ par un chemin $\gamma$. Choisissons une partition $t_0 =0 \leq t_1 \leq \ldots \leq t_{p+1} =1$ de l’intervalle $[0,1]$ de sorte qu’il existe des ouverts $V_0 , \ldots , V_p$ de cartes $\varphi_0 , \ldots , \varphi_p$ tels que $\gamma ([t_i , t_{i+1}] ) \subset V_i$. Soient $g_i$ les éléments de $G$ tels que $\varphi_i = g_{i+1} \circ \varphi_{i+1}$ au voisinage de $\gamma (t_{i+1})$. Posons alors

$$D(v) = g_1 \circ \ldots \circ g_p (\varphi_p (v)).$$

On vérifie, grâce au lemme ci-dessous que, à partition fixée, $D(v)$ ne dépend pas du choix des cartes $\varphi_1 , \ldots , \varphi_p$. En effet, si on a d’autres cartes $\varphi_i '$, avec $\varphi_0 ' = \varphi_0$, on a l’égalité, avec $h_i$ dans $G$, $\varphi_i ' = h_i \circ \varphi_i$ au voisinage de $\gamma ([t_i , t_{i+1}])$ d’où $g_i ' = h_{i-1}^{-1} \circ g_i \circ h_i$.

On en déduit que $D(v)$ ne dépend pas de la partition et enfin que $D(v)$ ne dépend pas du lacet choisi car $V$ est simplement connexe.

Démonstration. L’ensemble $\{ w \in W \; : \; \varphi \mbox{ et } \varphi' \mbox{ coïncident dans un voisinage de } w \}$ est ouvert et fermé.

C.Q.F.D.

$$ $$

Une conséquence de ce lemme est que si $D' : V \rightarrow X$ est un autre $(G,X)$-morphisme, alors il existe $g$ dans $G$ tel que $D' = g \circ D$.

Il se pourrait a priori que $D$ ne soit pas un difféomorphisme global. La proposition suivante permet toutefois de montrer que si $V$ est (métriquement) complète, l’application $D$ est bien un difféomorphisme et donc une isométrie.

Démonstration. La métrique (riemannienne) sur $X$ induit une métrique sur $V$, celle pour laquelle les cartes de la $(G,X)$-structure sont des isométries.

Pour montrer que $D$ est un revêtement, il suffit alors de montrer la propriété de relèvement des chemins :

Pour tout point $v$ de $V$ et tout chemin $C^1$ $c:[0,1] \rightarrow X$ tel que $c(0) = D(v)$, il existe un chemin $C^1$ $\tilde{c} : [0,1] \rightarrow V$ tel que $\tilde{c} (0) = v$ et $c=D\circ \tilde{c}$.

Pour cela, notons $[0, t_0]$ le plus grand intervalle sur lequel un tel relèvement existe. Si $t_0 <1$, l’intervalle est ouvert en $t_0$. Maintenant $V$ est complète. Et le chemin $\tilde{c}([0, t_0 [)$ est de longueur finie (car $D$ est une isométrie locale). Donc la limite $\lim_{t \rightarrow t_0} \tilde{c} (t)$ existe. Contradiction.

C.Q.F.D.

L’application $D$ est donc un revêtement. Or $V$ est connexe et $X$ simplement connexe. Donc $D$ est un difféomorphisme global. Mais $D$ est un $(G,X)$-morphisme et donc $D$ est une isométrie globale. L’espace $X$ est donc l’unique (à isométrie près) $(G,X)$-variété complète et simplement connexe.

$$ $$

Une version faible du théorème du domaine fondamental

Démonstration. Le quotient $[P]$ est une variété euclidienne si $X=\mathbb{R}^n$, sphérique si $X=\mathbb{S}^n$ et hyperbolique si $X=\mathbb{H}^n$. Puisque $[P]$ est compacte cette variété est en outre (métriquement) complète. Tout revêtement de $[P]$ est donc encore une variété euclidienne, sphérique ou hyperbolique complète. Le fait ci-dessus identifie en particulier $X$ au revêtement universel de $[P]$. Et le groupe $\Gamma$ des automorphismes de ce revêtement est un sous-groupe discret de $G$ qui s’identifie au groupe fondamental de $[P]$.

Finalement, la version topologique du théorème du domaine fondamental identifie le revêtement universel de $[P]$ à un pavage abstrait $E$. Le difféomorphisme $E \to X$ envoie un pavé fondamental dans $E$ sur le polyèdre $P \subset X$. On conclut que $P$ est un domaine fondamental pour $\Gamma$ et que $\Gamma$ est engendré par $\Phi$ [5].

C.Q.F.D.

Démonstration de la version générale

Si $x$ est un point de $P$ extérieur à son $(n-2)$-squelette, autrement dit si $x$ appartient à l’intérieur de $P$ ou à l’intérieur d’une face de codimension $1$, alors le cycle $[x]$ a évidemment un angle solide $\omega [x]$ égal à $1$. L’hypothèse sur les angles autour des faces de codimension $2$ dans le théorème du domaine fondamental implique que si $x$ appartient à l’intérieur d’une face de codimension $2$, le cycle $[x]$ a encore un angle solide $\omega [x]$ égal à $1$. La version faible du théorème implique donc la version forte lorsque $n=2$. Pour démontrer la version générale on procède par récurrence sur $n$. On se contente ici de démontrer le théorème lorsque $P$ est de dimension $n=3$.

Il s’agit de vérifier que sous l’hypothèse sur les angles autour des faces de codimension $2$ dans le théorème du domaine fondamental l’appariement $\Phi$ est nécessairement propre.

Puisque $P$ est supposé de dimension $3$, seul un cycle de sommets peut a priori avoir un angle solide différent de 1. Toutefois si $[x] = \{ x_1 , \ldots , x_m \}$ est un cycle de sommets de $P$, chaque sphère $S(x_i , r)$ (où $r$ est choisi comme dans la définition des angles solides) intersecte $P$ selon un polyèdre sphérique. Et le théorème du domaine fondamental (en dimension 2 mais étendu à une réunion finie de polyèdres) s’applique [6] pour montrer que ces polyèdres se recollent en un pavage de la sphère $\mathbb{S}^2$. [7] L’angle solide $\omega [x]$ est donc nécessairement égal à 1.

Le cas général se traite de la même manière en appliquant récursivement le théorème du domaine fondamental.

Le théorème pour la sphère $\mathbb{S}^3$

Dans la sphère $\mathbb{S}^3$ on obtient en particulier le théorème suivant que l’on applique ici à un recollement du cube et là à un recollement du dodécaèdre.