|
> Exemples de dimension 3 > Fibrés sur le cercle > Une variété hyperbolique de dimension 3 qui fibre sur le cercle (...) Une variété hyperbolique de dimension 3 qui fibre sur le cercle ...... et un théorème de Ian Agol et Dani Wise |
Le premier but de cet article est de donner une démonstration « visuelle » du théorème suivant. Nous supposons ici le lecteur familier avec la géométrie hyperbolique.
Il existe une variété hyperbolique compacte qui fibre sur le cercle.
Ce théorème était surprenant en 1977, s’il ne vous surprend pas vous êtes trop cultivé !
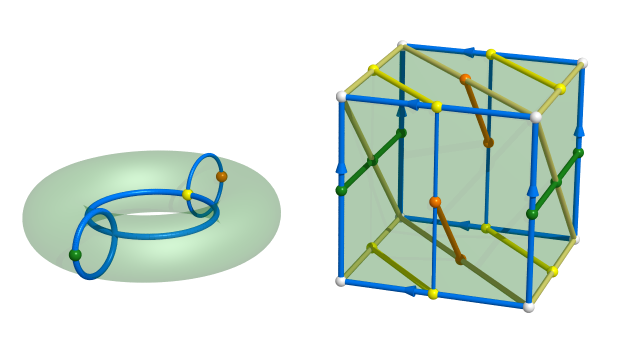
Partons du tore de dimension 3
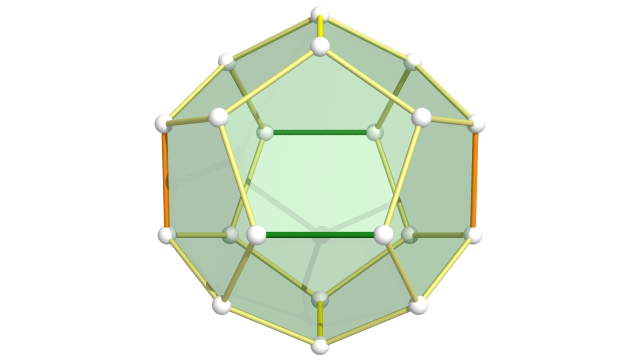
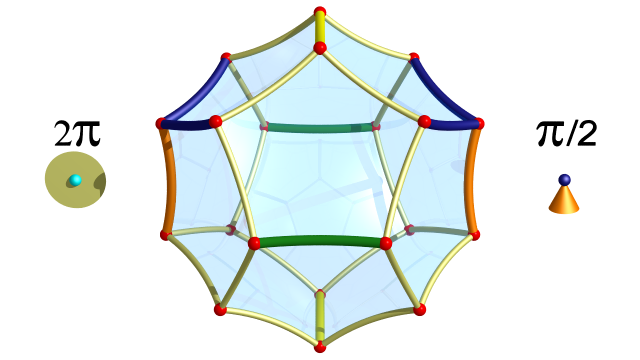
On peut voir le tore $\mathbb{T}^3$ de dimension $3$ comme un quotient du cube mais aussi comme un quotient du dodécaèdre :
Parmi les 30 arêtes du dodécaèdre, 24 sont identifiées par groupes de 4 et 6 sont identifiées par paires.
Le tore une variété hyperbolique ?
Dans l’espace hyperbolique, il y a toute une famille de dodécaèdres réguliers. Un « petit » dodécaèdre est presque euclidien d’angle dièdre $\arccos (-1/\sqrt{5}) \approx 116,56505^{\circ}$ et un dodécaèdre idéal (dont les sommets sont à l’infini) a pour angle dièdre $60^{\circ}$.
Dans l’espace hyperbolique, il existe donc un dodécaèdre régulier à angles droits $\mathcal{D}$.
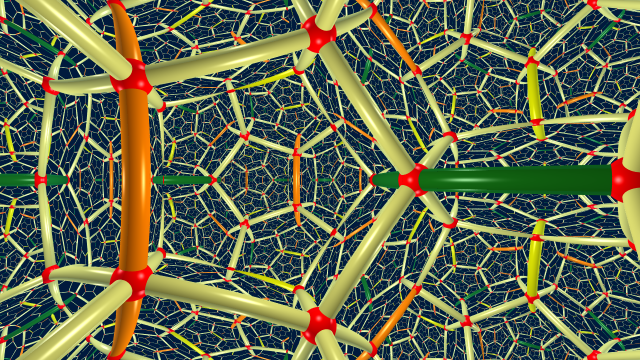
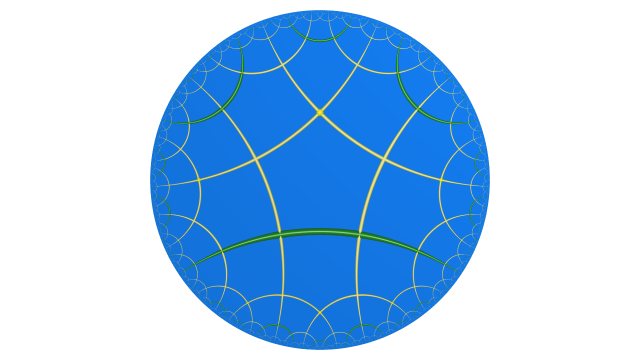
Les réflexions dans les faces de $\mathcal{D}$ permettent de paver tout l’espace hyperbolique $\mathbb{H}^3$ de dimension $3$.
Comme dans le pavage de l’espace euclidien par des cubes, autour de chaque arête il y a 4 dodécaèdres et autour de chaque sommet il y a 8 dodécaèdres. Les arêtes coloriées s’assemblent pour former des géodésiques jaunes, oranges et vertes.
Les translations euclidiennes qui identifient les faces opposées du cube pour former un tore induisent six paires d’identifications de faces de $\mathcal{D}$. On peut réaliser ces transformations par des isométries de $\mathbb{H}^3$. On note $G$ le groupe qu’elles engendrent. C’est un sous-groupe d’indice fini du groupe engendré par les réflexions dans les faces de $\mathcal{D}$ et dans les 3 plans passant par les 3 paires d’arêtes coloriées.
Le groupe $G$ a de la torsion. Tout élément de torsion est conjugué à une rotation d’angle $\pi$ autour de l’une des géodésiques jaunes, oranges et vertes.
Le quotient $G \backslash \mathbb{H}^3$ est donc singulier.
Le quotient $G \backslash \mathbb{H}^3$ est un orbifold d’espace topologique sous-jacent le tore de dimension $3$ et de lieu singulier la réunion disjointe de trois cercles parallèles aux trois axes et groupe d’isotropie $\mathbb{Z} / 2\mathbb{Z}$ le long du lieu singulier.
Construction d’une variété hyperbolique
On veut construire un sous-groupe d’indice fini de $G$ qui soit sans torsion. Pour cela on va utiliser le fait que $G$ contient « beaucoup » de groupes de surfaces.
Le pavage de $\mathbb{H}^3$ par des dodécaèdres à angles droits induit un pavage par pentagones à angles droits sur chaque plan supportant une face de $\mathcal{D}$.
Les réflexions dans le faces de $\mathcal{D}$ engendrent un groupe de Coxeter à angles droits
$$C = \langle x_F \ (F \mbox{ face de } \mathcal{D}) \; \big| \; x_F^2 , \ [x_F , x_{F'} ] \ (F \cap F' \mbox{ arête de } \mathcal{D}) \rangle$$
qui contient plusieurs copies du groupe $P$ engendré par les réflexions dans les faces d’un pentagone hyperbolique à angles droits.
La projection orthogonale sur un plan supportant une face de $\mathcal{D}$ induit une rétraction
$$r:C \to P.$$
Le groupe $G \cap C$ est d’indice fini dans $G$.
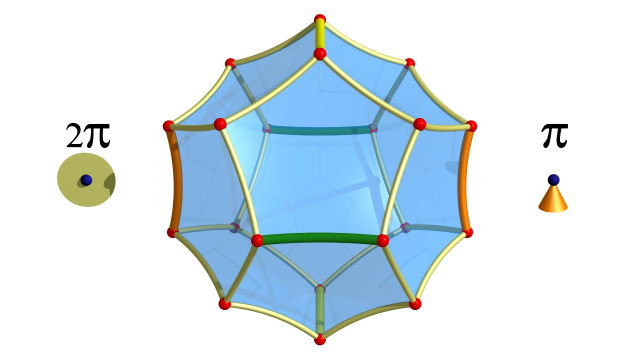
Un élément d’ordre fini de $G \cap C$ est une rotation d’angle $\pi$ autour d’une arête jaune, orange ou verte. L’image d’une telle rotation autour d’une arête jaune dans le groupe $P$ est la symétrie autour du sommet (jaune) correspondant.
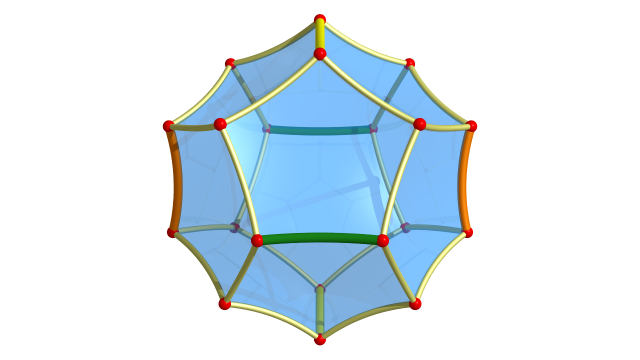
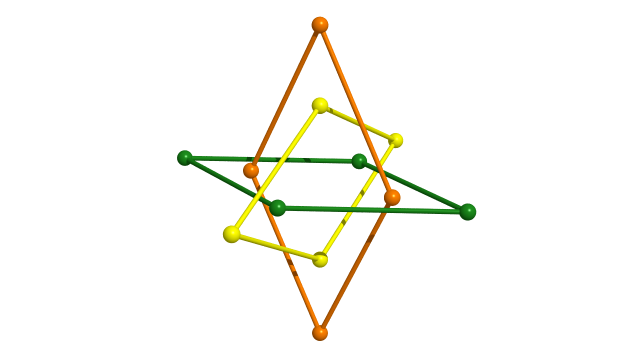
Dans le plan hyperbolique on peut assembler 4 pentagones en un octogone.
Le groupe $P$ contient un sous-groupe $F$ d’indice $4$, qui identifie par paires les côtés verts de l’octogone en préservant l’orientation et les côtés oranges en renversant l’orientation.
Le groupe $F$ est sans torsion.
Le groupe $F$ est isomorphe au groupe fondamental d’une surface non-orientable de caractéristique d’Euler
$$\chi = 2 -4 +1 = -1.$$
Le revêtement d’orientation de cette surface est de genre $2$, comme le montre aussi l’animation suivante.
L’intersection $G\cap r^{-1} (F)$ est donc un sous-groupe d’indice fini de $G$ qui ne contient aucune rotation autour d’un arête jaune. En procédant de la même manière avec les arêtes oranges et vertes on construit un sous-groupe $G'$ d’indice fini et sans torsion dans $G$.
$$ $$
La quotient $ V= G' \backslash \mathbb{H}^3$ est un variété hyperbolique compacte.
$$ $$
Suivant une idée de William Thurston, exposée par Dennis Sullivan à Bourbaki, on montre maintenant que la variété $V$ fibre sur le cercle.
Une variété qui fibre sur le cercle
L’image du plan d’équation $x+y+z=0$ dans le tore $\mathbb{Z}^3 \backslash \mathbb{R}^3$ intersecte transversalement les cercles jaune, orange et vert. Les plans parallèles $x+y+z = t$, avec $t\in [0,1]$, forment un feuilletage (en tores de dimension $2$) de $\mathbb{Z}^3 \backslash \mathbb{R}^3$ dont chaque feuille intersecte transversalement les cercles jaune, orange et vert.
L’orbifold hyperbolique $G \backslash \mathbb{H}^3$ fibre au-dessus du cercle en orbifolds de dimension $2$ d’espace topologique sous-jacent le tore de dimension $2$ et de lieu singulier la réunion disjointe de trois points et groupe d’isotropie $\mathbb{Z} / 2\mathbb{Z}$ en chacun de ces points.
La variété $V=G' \backslash \mathbb{H}^3$ est un revêtement fini du tore de dimension $3$, ramifié d’ordre $2$ au-dessus du lieu singulier de l’orbifold fibré $G \backslash \mathbb{H}^3$.
$$ $$
La préimage de chaque fibre dans $G \backslash \mathbb{H}^3$ est une surface obtenue comme revêtement du tore de dimension $2$, ramifié au-dessus au-dessus de 3 points.
La variété $V$ fibre donc en surfaces au-dessus du cercle.
$$ $$
Savoir qu’une variété fibre sur le cercle éclaire sa topologie $\ldots$ mais pas tant que ça ! Par exemple : si $V$ fibre sur le cercle alors $\pi_1 (V) \twoheadrightarrow \mathbb{Z}$. Mais existe-t-il un revêtement fini $V' \to V$ tel que
$$\pi_1 (V' ) \twoheadrightarrow \mathbb{Z}^2 \ ? \quad \mathbb{Z} * \mathbb{Z} \ ?$$
$$ $$
Les réponses à ces questions sont difficiles en général. La raison en est que les fibres sont plongées de manière très compliquée dans la variété $V$.
On peut représenter une élévation à $\mathbb{H}^3$ d’une fibre dans $V$ par une surface obtenue en recollant des hexagones.
La surface obtenue est géométriquement très compliquée, comme le montre la vidéo suivante.
Il s’avère plus commode d’utiliser les surfaces portées par les faces de $\mathcal{D}$.
La projection orthogonale sur un plan supportant une face de $\mathcal{D}$ induit en effet une rétraction
$$r: C \to P.$$
Il existe donc un revêtement fini $V' \to V$ tel que
$$\pi_1 (V' ) \twoheadrightarrow \mathbb{Z} * \mathbb{Z} \quad (\mbox{et donc aussi } \mathbb{Z}^2 ).$$
Le théorème d’Agol et Wise
Ce point de vue se généralise :
Soit $V$ une variété hyperbolique compacte de dimension $3$ alors il existe un revêtement fini $V' \to V$ tel que $\pi_1 (V')$ soit plongé de manière quasi-convexe (au sens des mots) dans un groupe de Coxeter à angles droits abstrait associé à un graphe simplicial fini $\Gamma$ :
$$ \pi_1 (V) \stackrel{q.c.}{\hookrightarrow} \mathrm{COX} (\Gamma ) = \langle x_s , \ s \in \mbox{S} (\Gamma) \; \big| \; x_s^2, \ \ [x_s , x_{s'} ], \ (s,s' ) \in \mbox{A} (\Gamma ) \rangle.$$
Ce que l’on a observé dans le groupe $C$ s’étend assez naturellement aux groupes de Coxeter à angles droits abstraits :
Soit $H$ un sous-groupe plongé de manière quasi-convexe dans un groupe de Coxeter à angles droits abstrait $\mathrm{COX} (\Gamma)$ avec $\Gamma$ fini. Alors il existe un sous-groupe d’indice fini $G < \mathrm{COX} (\Gamma)$ contenant $H$ et une rétraction
$$r : G \to H.$$
Comme pour la rétraction $C \to P$, il est fondamental ici que le groupe de Coxeter soit à angles droits.
Finalement un argument de « ping-pong » montre que si $V$ est une variété hyperbolique compacte alors $\pi_1 (V)$ contient un sous-groupe libre non-abélien et quasi-convexe.
Et on conclut qu’il existe un revêtement fini $V' \to V$ tel que
$$\pi_1 (V' ) \twoheadrightarrow \mathbb{Z} * \mathbb{Z} \quad (\mbox{et donc aussi } \mathbb{Z}^2 ).$$
$$ $$
Le théorème d’Agol et Wise éclaire la structure des groupes fondamentaux des variétés hyperboliques de dimension $3$. Finalement, Agol en déduit même :
Soit $V$ une variété hyperbolique compacte de dimension $3$ alors il existe un revêtement fini $V' \to V$ tel que $V'$ fibre sur le cercle.
Épilogue
Le groupe $U$ engendré par les rotations d’angles $\pi/2$ autour des géodésiques jaunes, oranges et vertes du pavage de $\mathbb{H}^3$ normalise le groupe de Coxeter $C$.
Le quotient $U \backslash \mathbb{H}^3$ est un orbifold compact de groupe d’isotropie $\mathbb{Z} / 4\mathbb{Z}$ le long du lieu singulier. C’est aussi un quotient de $V$.
L’espace topologique sous-jacent à cet orbifold est la sphère $\mathbb{S}^3$ et le lieu singulier est un entrelacs isotope aux anneaux borroméens.
La variété $V$ est donc un revêtement fini de $\mathbb{S}^3$, ramifié au-dessus des entrelacs borroméens, avec ramification cyclique de degré $4$ au-dessus de chaque brin.
C’est en fait le cas de toute variété compacte de dimension $3$ :
Toute variété compacte orientable de dimension $3$ s’obtient comme revêtement fini de $\mathbb{S}^3$, ramifié au-dessus des entrelacs borroméens, avec ramification cyclique de degré $ \leq 4$ au-dessus de chaque brin.
$$ $$
Autrement dit, toute variété compacte orientable de dimension $3$ est homéomorphe à l’espace topologique sous-jacent à un orbifold $\Gamma \backslash \mathbb{H}^3$, où $\Gamma$ est un sous-groupe d’indice fini de $U$.
On dit que le groupe $U$ est universel.