Scindement de Heegaard d’une variété polyédrique

Une variété polyédrique (c’est-à-dire un espace d’identification d’un polyèdre qui se trouve être une variété) possède un scindement de Heegaard naturel (de genre égal à la moitié du nombre de faces du polyèdre), que l’on peut coder très simplement par un diagramme de Heegaard « généralisé ». [1]

Illustrons ceci sur l’exemple de la variété dodécaédrique de Poincaré.

Rappelons que celle-ci est obtenue en identifiant les faces opposées d’un dodécaèdre par une translation suivie d’une rotation d’un dixième de tour [2]. Ces identifications déterminent une classe d’équivalence de 3-cellule, six classes de faces, dix classes d’arêtes (représentées sur la figure ci-dessous) et cinq classes de sommets, auxquelles vont correspondre une 0-anse, six 1-anses, dix 2-anses et cinq 3-anses.

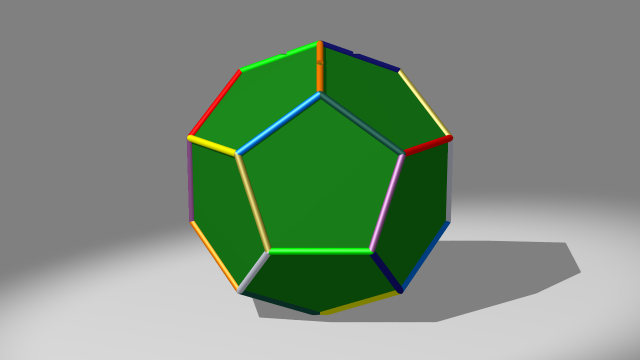
Dans la vidéo suivante, on commence par « détacher » les 3-anses.

On commence par retirer au dodécaèdre un voisinage des quatre sommets d’une même classe. Au quotient, ces quatre tétraèdres se recollent en une boule de dimension 3 (attention, ce ne serait pas vrai pour un espace polyédrique qui ne serait pas une variété, mais le fait que l’espace dodécaédrique soit une variété signifie précisément ceci). Si l’on fait de même pour les autres classes de sommets, on a donc retiré à notre variété cinq boules. Notons $V_2$ le complémentaire. Pour reconstruire la variété, il s’agit donc de recoller à $V_2$ cinq boules le long de leur bord, i.e. d’attacher à $V_2$ cinq 3-anses.

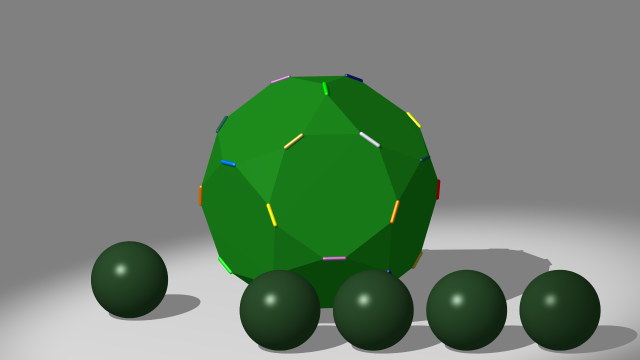
On s’intéresse ensuite aux 2-anses.

On retire à présent au dodécaèdre déjà tronqué un voisinage des trois arêtes d’une même classe (ou ce qu’il en reste). Au quotient, ces trois pièces se recollent le long de leurs faces adjacentes à l’arête. L’objet obtenu est à nouveau topologiquement une boule, mais cette fois, pour reconstruire $V_2$, on ne recolle l’objet que le long d’une partie annulaire de son bord, la partie vert foncé sur l’image ci-dessous. Autrement dit, pour reconstruire $V_2$, on attache une 2-anse. Pour décrire une telle opération, il suffit de spécifier le lacet auquel va être recollé un lacet méridien de l’anse, matérialisé ici en jaune, comme la classe d’arête considérée. Sur le dodécaèdre tronqué (avant passage au quotient) ce lacet correspond aux trois segments jaunes ci-dessous, un par élément de la classe d’arêtes.

Notons $V_1$ la variété à bord obtenue en retirant un voisinage de toutes les arêtes restantes. $V_2$ s’obtient donc à partir de $V_1$ en attachant dix 2-anses.

$V_1$, maintenant, est un corps en anses (à six anses pour être précis). En effet, $V_1$ s’obtient à partir du dodécaèdre tronqué en identifiant par paires opposées ce qu’il reste des faces, soit douze disques disjoints (des pentagones sur l’image ci-dessus). Or recoller deux tels disques revient topologiquement à attacher une 1-anse entre ces deux disques. Si l’on retire à $V_1$ ces six 1-anses, ce qui revient à supprimer les identifications entre les faces du dodécaèdre tronqué, il nous reste $V_0$, une boule, ce qui donne bien la décomposition en anses annoncée au départ. Les corps en anses du scindement de Heegaard correspondant sont $V_1$ et l’adhérence de son complémentaire (qui est bien un corps en anses, s’en convaincre).

Remarquons enfin que le dodécaèdre tronqué de l’image ci-dessus avec ses courbes d’attachement nous fournit une sorte de diagramme de Heegaard « généralisé » de ce scindement.

Sur un vrai diagramme, le scindement étant de genre 6, il n’y aurait que six couleurs de courbes. Ici il y en a dix. Cela correspond au fait qu’ici le second corps en anses n’est pas naturellement décrit comme l’union de six anses et d’une boule mais comme celle de dix anses (une par classe d’arêtes) et cinq boules (une par classe de sommets). Néanmoins, ce diagramme décrit complètement la variété : on obtient celle-ci en attachant six 1-anses à la boule reliant les disques opposés, puis les courbes colorées déterminent le lieu d’attachement de dix 2-anses, et l’on a plus qu’à recoller des boules le long des sphères du bord restant (la façon de recoller ces boules n’a pas besoin d’être précisée ; quel que soit le recollement, on obtiendra des variétés homéomorphes).