Deux décompositions de la variété dodécaédrique de Poincaré

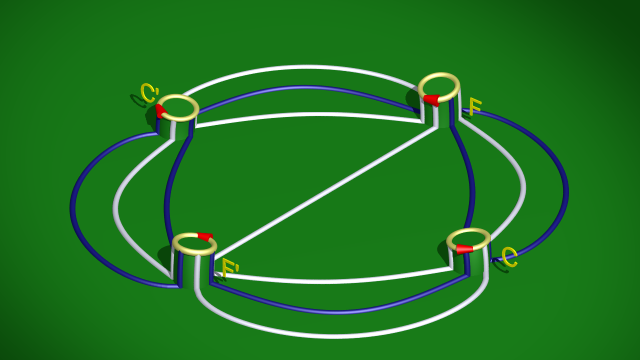
Toute variété de dimension 3 peut être obtenue comme recollement d’anses — ou scindement de Heegaard — mais aussi comme le résultat d’une chirurgie de Dehn. On montre ici que l’espace dodécaédrique de Poincaré (défini par identification des faces opposées d’un dodécaèdre) peut-être obtenu en recollant les six morceaux suivants

selon le diagramme de Heegaard

Le but de cet article est de démontrer en images le théorème suivant.

Démonstration. Le diagramme de Heegaard est un plan de construction qui explique comment fabriquer une variété de dimension 3 en recollant les six pièces de la première image : une boule (ou 0-anse), deux cylindres (ou 1-anses), deux disques épaissis (ou 2-anses) et encore une boule (ou 3-anse). On colle d’abord les deux 1-anses sur la 0-anse, puis on colle les 2-anses, et enfin la 3-anse. À chaque étape, on colle les faces foncées sur le résultat de l’étape précédente dont le bord est vert clair. Dans la variété finale, l’union des deux dernières anses à attacher (une 2-anse et une 3-anse) forme un tore plein. La présente démonstration consiste à montrer que son complémentaire, l’union des quatre autres anses (une 0-anse, deux 1-anses et une 2-anse), est homéomorphe au complémentaire du nœud de trèfle dans $\mathbb{S}^3$ — ce qui signifie précisément que notre variété est obtenue par chirurgie sur le nœud de trèfle — et à vérifier que la courbe de chirurgie est bien celle annoncée.

Dans les vidéos qui suivent on représente la première étape de construction de la variété : le recollement des deux cylindres (1-anses) sur la première boule (0-anse). Cette opération peut s’effectuer de façon tout à fait abstraite mais on peut aussi, pour la visualiser, et en prévision de la suite, la plonger dans la 3-sphère, dont la vidéo montre une projection stéréographique. Il faut alors penser le plan vert portant le diagramme comme le bord de la 0-anse, qui, au début du film, occupe le demi-espace inférieur. Un changement de projection envoie ce demi espace sur le complémentaire d’une boule. Nous nous trouvons donc, à l’issue de la première séquence, à l’intérieur de la 0-anse, qui devrait être lui aussi vert et opaque, mais nous avons dû le vider de sa « chair » pour en voir le bord !

C’est sur la face du bord invisible pour le spectateur que l’on doit recoller les 1-anses. Là encore, cette opération est réalisable dans $\mathbb{S}^3$. Topologiquement, elle équivaut à identifier par paires les disques du bord portant la même lettre. Ces disques ne doivent pas être identifiés n’importe comment. Un diagramme de Heegaard « classique » indique comment les extrémités des courbes de couleurs aboutissant aux disques doivent être identifiées. En fait, un point marqué (représenté ici par une flèche rouge) sur chaque bord de disque suffit à lever toute ambiguïté sur la façon dont ces courbes doivent être recollées (ou, de façon équivalente, prolongées sur le bord des anses). Après attachement des 1-anses, notre variété en construction est à présent un corps en anses de genre 2. Comme nous avons évidé la 0-anse, nous évidons les 1-anses, on ne voit donc plus que le bord de notre corps en anses mais attention : celui-ci est la composante non bornée du complémentaire de cette surface de genre 2 (puisqu’il contient l’observateur !), et non la composante bornée comme on a l’habitude de se le représenter.

Les deux courbes simples fermées blanche et bleue sur la surface, dernières et principales données du diagramme de Heegaard, indiquent comment recoller les deux pièces suivantes, à savoir deux disques épaissis ou 2-anses.

L’un de ces recollements, celui de la courbe bleue, peut être réalisé dans $\mathbb{S}^3$. Ce n’est pas clair à ce stade, mais nous allons pour cela déformer la surface — ou plutôt le corps en anses — de manière à simplifier la courbe bleue. On pourra alors lui recoller un disque épaissi avec pour conséquence de modifier profondément ce corps en anses puisqu’il deviendra alors précisément le complémentaire du nœud de trèfle.

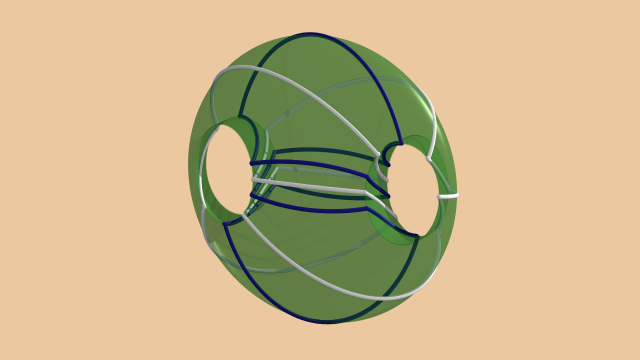
Commençons par déformer le corps en anses pour lui donner une forme plus « standard ».

Le résultat est le suivant :

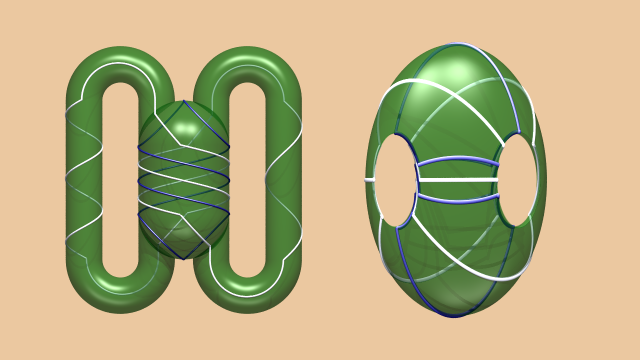
La courbe bleue ne passe que par la « partie centrale » de la surface de notre corps en anses. En (dé)vissant cette partie centrale, il est alors possible de simplifier la courbe bleue, au prix de « nouer » le corps en anses.

On obtient l’image suivante :

On peut à présent recoller une 2-anse (un disque épaissi) le long de la courbe bleue. Rappelons encore une fois que, nous, spectateurs, nous trouvons à l’intérieur du corps en anses. Le complémentaire (dans $\mathbb{S}^3$) du corps en anses est donc, sur nos images, la zone située à l’intérieur de la surface représentée. La 2-anse doit donc être collée à l’intérieur de la sphère (creuse) qui se trouve au centre de l’image.

La variété obtenue après ce recollement est l’extérieur du nœud de trèfle (cf. l’« exercice mental » ci-dessous). La variété de dimension 3 décrite par le diagramme de Heegaard dont nous sommes partis s’obtient en recollant le deuxième disque épaissi le long de la courbe blanche, puis en bouchant le bord sphérique obtenu avec la 3-anse restante. Cela revient donc à faire une chirurgie de Dehn le long du nœud de trèfle.

Finalement, dans la vidéo suivante, on déforme, par isotopie, la courbe blanche pour montrer qu’elle parcourt une fois (longitudinalement) la projection planaire du nœud et tourne deux fois autour du méridien.

Un petit exercice mental, qui consiste à « lever une poignée » permet de vérifier qu’on obtient bien la courbe de chirurgie annoncée :

C.Q.F.D.

$$ $$

Un résumé en image de la démonstration.

$$ $$

Démonstration.

Pour déterminer le paramètre de la chirurgie, il faut comparer la courbe :

à celle tracée par une surface de Seifert. C’est l’objet de l’animation suivante.

On constate que la courbe tracée par une surface de Seifert parcourt une fois la projection planaire du nœud de trèfle et tourne trois fois autour du méridien.

Finalement la courbe blanche se décompose en la somme du bord de la surface de Seifert et d’un méridien parcouru une fois dans le sens négatif. Et la chirurgie a donc pour paramètre -1.