Différentes présentations du groupe fondamental de la variété dodécaédrique de Poincaré

À chaque scindement de Heegaard d’une 3-variété on peut associer une présentation de son groupe fondamental, dans laquelle les 1-anses sont les générateurs et les 2-anses donnent les relations. [1]

On se propose ici de comprendre différentes présentations du groupe fondamental $\widetilde{I}=\pi_1 (\Sigma )$ de la variété dodécaédrique de Poincaré $\Sigma$ correspondant aux différentes décompositions en anses rencontrées ici.

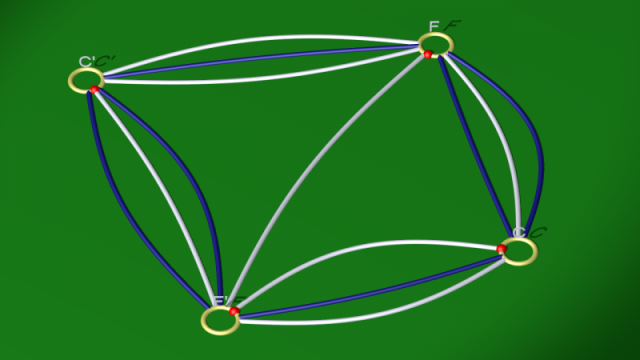
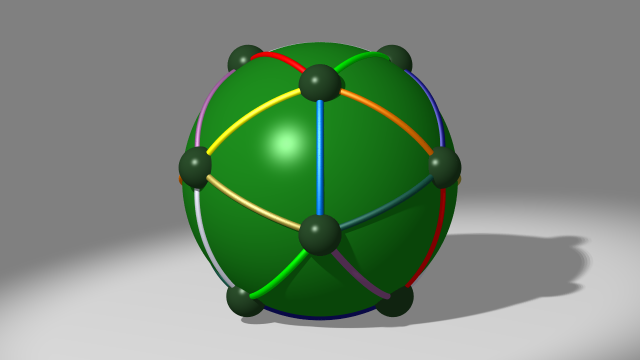
Partons de la variété dodécaédrique de Poincaré, définie en identifiant par paires les faces opposées d’un dodécaèdre via une translation suivie d’une rotation d’un dixième de tour [2], et du diagramme de Heegaard qui lui est naturellement associé en tant que variété polyédrique

$$ $$

Notons $a$ le générateur associé à la 1-anse $A,A'$ parcourue de $A$ vers $A'$, puis $b$ le générateur associé à la 1-anse $B,B'$ et ansi de suite jusqu’à $f$, comme sur la vidéo suivante [3].

$$ $$

On a dix relations, toutes de longueur trois. Elles correspondent aux dix 2-anses, et donc aux dix courbes de couleurs le long desquelles on attache ces 2-anses. Les voici :

$$\begin{array}{ll} \mbox{courbe vert foncé} & fca^{-1}\\ \mbox{courbe blanche} & eba^{-1}\\ \mbox{courbe vert clair} & dfa^{-1}\\ \mbox{courbe bleu foncé} & cea^{-1}\\ \mbox{courbe jaune} & bda^{-1}\\ \mbox{courbe rouge} & ecd^{-1}\\ \mbox{courbe bleu clair} & fde^{-1}\\ \mbox{courbe mauve} & bef^{-1}\\ \mbox{courbe dorée} & cfb^{-1}\\ \mbox{courbe orange} & dbc^{-1} \end{array}$$

On retrouve la présentation vue ici.

Une présentation avec deux générateurs et deux relations

On suit les différentes étapes de la simplification de la décomposition en anses.

1. La première étape consiste à éliminer des anses complémentaires. Du point de vue algébrique, cela revient à utiliser une relation pour éliminer un générateur ou éliminer des relations redondantes. On commence par éliminer la 1-anse $A,A'$ avec la 2-anse correspondant à la courbe vert foncé. Cela correspond à expliciter le générateur $a$ depuis la première relation, ce qui donne $a=fc$. On peut alors oublier $a$ en le remplaçant par $fc$ dans les autres relations. Géométriquement cette substitution correspond au fait que, lorsque l’on fait glisser la 1-anse $A,A'$, les arcs qui lui sont attachés suivent et deviennent plus compliqués.

$$ $$

On aboutit à un nouveau jeu de neuf relations :

$$\begin{array}{ll} \mbox{courbe blanche} & eb(fc)^{-1}\\ \mbox{courbe vert clair} & df(fc)^{-1}\\ \mbox{courbe bleu foncé} & ce(fc)^{-1}\\ \mbox{courbe jaune} & bd(fc)^{-1}\\ \mbox{courbe rouge} & ecd^{-1}\\ \mbox{courbe bleu clair} & fde^{-1}\\ \mbox{courbe mauve} & bef^{-1}\\ \mbox{courbe dorée} & cfb^{-1}\\ \mbox{courbe orange} & dbc^{-1} \end{array}$$

2. De la même manière on explicite $d$ sous la forme $ec$ en utilisant la relation $ecd^{-1}$ (ce qui revient à éliminer la 1-anse $D,D'$ avec la 2-anse correspondant à la courbe rouge), pour aboutir aux relations :

$$\begin{array}{ll} \mbox{courbe blanche} & eb(fc)^{-1}\\ \mbox{courbe vert clair} & (ec)f(fc)^{-1}\\ \mbox{courbe bleu foncé} & ce(fc)^{-1}\\ \mbox{courbe jaune} & b(ec)(fc)^{-1}\\ \mbox{courbe bleu clair} & f(ec)e^{-1}\\ \mbox{courbe mauve} & bef^{-1}\\ \mbox{courbe dorée} & cfb^{-1}\\ \mbox{courbe orange} & (ec)bc^{-1} \end{array}$$

qui correspondent au diagramme

$$ $$

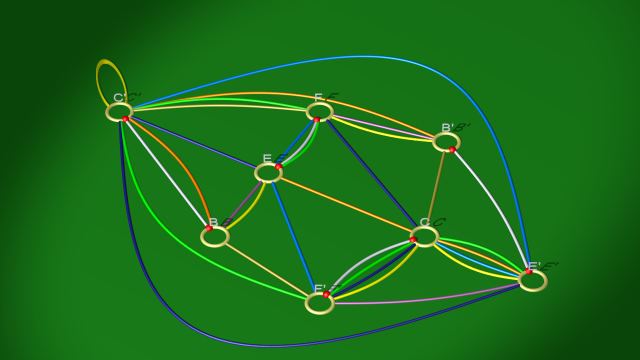
3. La relation $b(ec)(fc)^{-1}$ est équivalente à la relation $bef^{-1}$, modulo la simplification $becc^{-1}f\sim bef^{-1}$. Cette simplification correspond à éliminer la boucle jaune dans le diagramme ci-dessus. On aboutit alors aux relations

$$\begin{array}{ll} \mbox{courbe blanche} & eb(fc)^{-1}\\ \mbox{courbe vert clair} & (ec)f(fc)^{-1}\\ \mbox{courbe bleu foncé} & ce(fc)^{-1}\\ \mbox{courbe jaune} & bef^{-1}\\ \mbox{courbe bleu clair} & f(ec)e^{-1}\\ \mbox{courbe mauve} & bef^{-1}\\ \mbox{courbe dorée} & cfb^{-1}\\ \mbox{courbe orange} & (ec)bc^{-1} \end{array}$$

et au diagramme

$$ $$

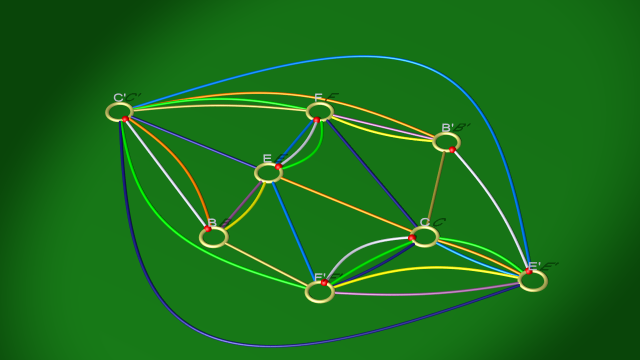
4. On explicite ensuite $b$ en utilisant la relation $bef^{-1}$ (ce qui correspond à simplifier la courbe mauve avec la 1-anse $BB'$). On aboutit aux relations suivantes :

$$\begin{array}{ll} \mbox{courbe blanche} & e(fe^{-1})(fc)^{-1}\\ \mbox{courbe vert clair} & (ec)f(fc)^{-1}\\ \mbox{courbe bleu foncé} & ce(fc)^{-1}\\ \mbox{courbe jaune} & (fe^{-1})ef^{-1}\\ \mbox{courbe bleu clair} & f(ec)e^{-1}\\ \mbox{courbe dorée} & cf(fe^{-1})^{-1}\\ \mbox{courbe orange} & (ec)(fe^{-1})c^{-1} \end{array}$$

qui correspondent au diagramme

$$ $$

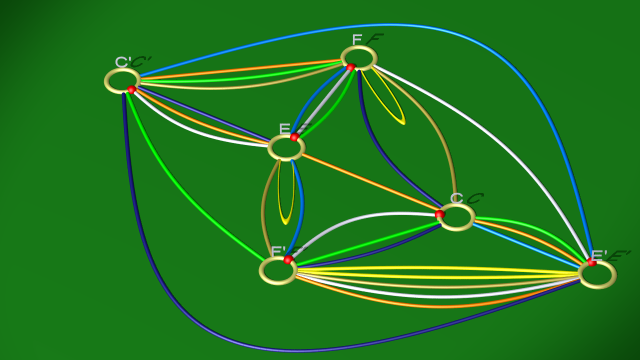
5. La relation $(fe^{-1})ef^{-1}$ est triviale ce qui correspond au fait que la courbe jaune est maintenant homotopiquement triviale dans le bord du corps en anses. On peut donc la supprimer. On aboutit aux relations

$$\begin{array}{ll} \mbox{courbe blanche} & e(fe^{-1})(fc)^{-1}\\ \mbox{courbe vert clair} & (ec)f(fc)^{-1}\\ \mbox{courbe bleu foncé} & ce(fc)^{-1}\\ \mbox{courbe bleu clair} & f(ec)e^{-1}\\ \mbox{courbe dorée} & cf(fe^{-1})^{-1}\\ \mbox{courbe orange} & (ec)(fe^{-1})c^{-1} \end{array}$$

et au diagramme

$$ $$

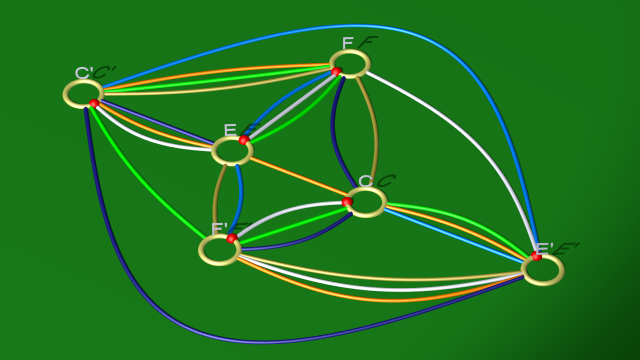
6. On explicite ensuite $e$ en utilisant la relation $cf(fe^{-1})^{-1}$ (ce qui correspond à éliminer la 1-anse $EE'$ avec la courbe dorée) pour aboutir aux relations suivantes :

$$\begin{array}{ll} \mbox{courbe blanche} & (f^{-1}c^{-1}f)(f(f^{-1}c^{-1}f)^{-1})(fc)^{-1}\\ \mbox{courbe vert clair} & ((f^{-1}c^{-1}f)c)f(fc)^{-1}\\ \mbox{courbe bleu foncé} & c(f^{-1}c^{-1}f)(fc)^{-1}\\ \mbox{courbe bleu clair} & f((f^{-1}c^{-1}f)c)(f^{-1}c^{-1}f)^{-1}\\ \mbox{courbe orange} & ((f^{-1}c^{-1}f)c)(f(f^{-1}c^{-1}f)^{-1})c^{-1} \end{array}$$

qui correspondent au diagramme

$$ $$

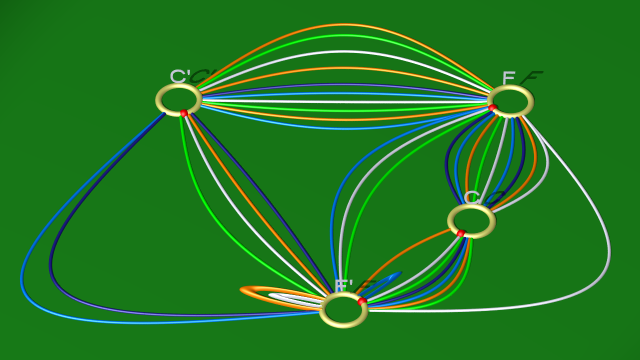
7. L’élimination des boucles blanche, bleu clair et orange correspond encore une fois à des simplifications des relations associées (respectivement la première, l’avant-dernière et la dernière relation ci-dessus). On aboutit aux relations :

$$\begin{array}{ll} \mbox{courbe blanche} & f^{-1}c^{-1}fcfc^{-1}f^{-1}\\ \mbox{courbe vert clair} & ((f^{-1}c^{-1}f)c)f(fc)^{-1}\\ \mbox{courbe bleu foncé} & c(f^{-1}c^{-1}f)(fc)^{-1}\\ \mbox{courbe bleu clair} & c^{-1}fcf^{-1}cf\\ \mbox{courbe orange} & f^{-1}c^{-1}fc^2fc^{-1} \end{array}$$

et au diagramme

$$ $$

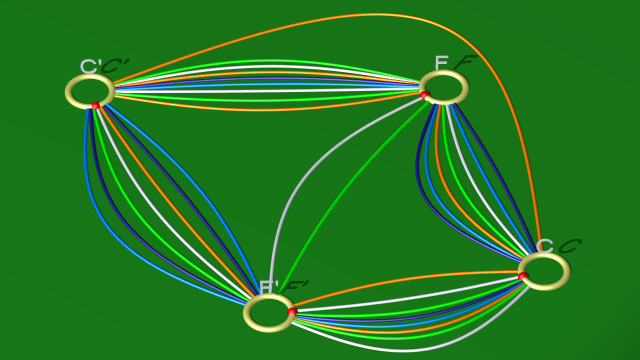
8. On remarque maintenant que la première et la deuxième, ainsi que la troisième et la quatrième sont équivalentes. Ceci correspond au fait que dans le diagramme les courbes blanche et vert clair, ainsi que les courbes bleu clair et bleu foncé, sont homotopes. On supprime donc les courbes vert clair et bleu clair, et les relations associées. Il nous reste donc les relations

$$\begin{array}{ll} \mbox{courbe blanche} & f^{-1}c^{-1}fcfc^{-1}f^{-1}\\ \mbox{courbe bleu foncé} & c(f^{-1}c^{-1}f)(fc)^{-1}\\ \mbox{courbe orange} & f^{-1}c^{-1}fc^2fc^{-1} \end{array}$$

et le diagramme

$$ $$

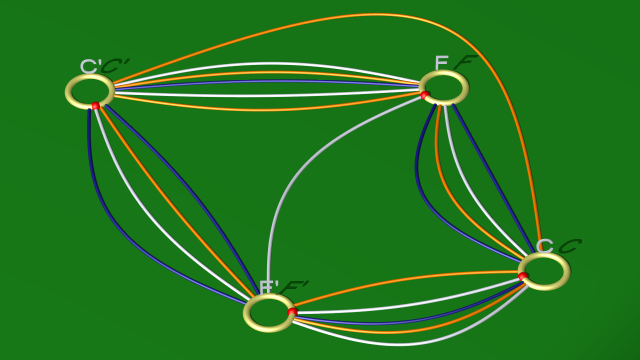
9. La dernière relation est, de son côté, conséquence des deux autres. On a en effet :

$$f^{-1}c^{-1}fc^2fc^{-1}=(f^{-1}c^{-1}fcfc^{-1}f^{-1}) \underbrace{(fcf^{-1}cfc^{-1})}_{(cf^{-1} c^{-1} fc^{-1} f^{-1} )^{-1}} .$$

Cela correspond au fait de compliquer dans un premier temps le diagramme pour faire suivre la courbe bleu foncé par la courbe orange pour obtenir une courbe parallèle à la blanche.

$$ $$

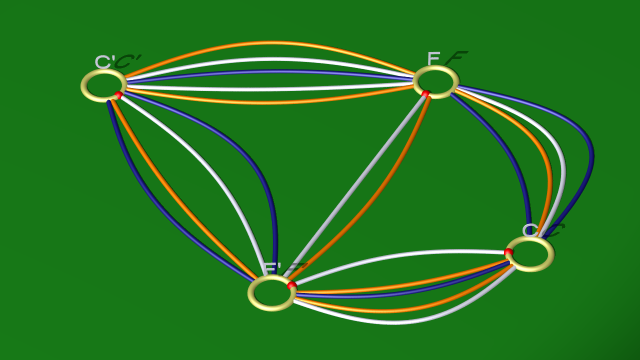
10. Les courbes blanche et orange sont maintenant homotopes ; on peut donc supprimer la courbe orange, et omettre la relation correspondante.
On aboutit alors au diagramme de Heegaard de genre 2 suivant :

$$ $$

et à la présentation suivante :

$$\langle c, f \mid f^{-1}c^{-1}fcfc^{-1}f^{-1}, \ cf^{-1}c^{-1}fc^{-1}f^{-1}\rangle$$

ou encore (en remplaçant la deuxième relation par son inverse et en conjuguant par $c$, ce qui revient simplement à parcourir la courbe bleu foncée dans l’autre sens)

$$\langle c, f \mid f^{-1}c^{-1}fcfc^{-1}f^{-1}, \ c^{-1}fcf^{-1}cf\rangle.$$

La présentation de Poincaré

On explique ici comment passer du scindement de Heegaard de genre 2 ci-dessus à celui donné par Poincaré.

La première étape consiste à faire un changement du choix du découpage du corps en anses. Plutôt que de lui enlever les 1-anses $CC'$ et $FF'$, on lui enlève deux 1-anses $CC'$ et $GG'$ comme indiqué plus bas. Le nouveau découpage correspond au diagramme suivant :

$$ $$

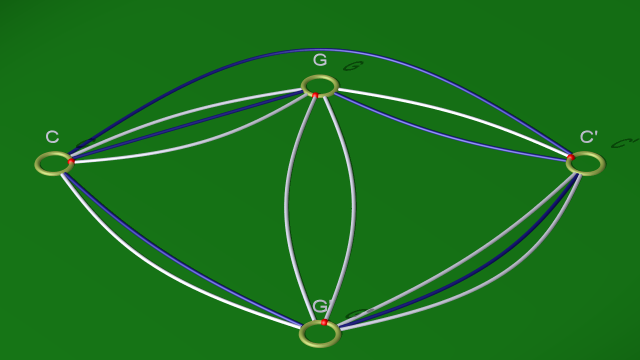
Du point de vue de la présentation du groupe fondamental, cela correspond à faire un changement de générateurs. Cela se voit mieux en raisonnant avec des lacets. Fixons donc un point base extérieur aux 1-anses $CC'$, $FF'$ et $GG'$ et identifions les générateurs correspondants $c$, $f$ et $g$ à des lacets comme sur les figures ci-dessous. [4] On passe des générateurs $f$ et $c$ aux nouveaux générateurs $g=f^{-1}$ et $\tilde c=f^{-1}c$. En effet, avant le changement de découpage le corps en anses et les lacets $c$ et $f$ étaient comme sur le dessin suivant :

$$ $$

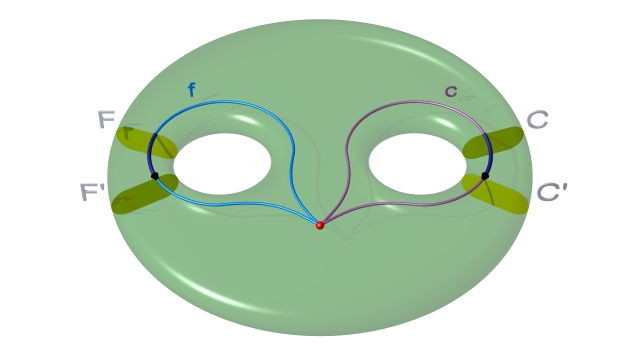
Et le changement de découpage aboutit au dessin suivant :

$$ $$

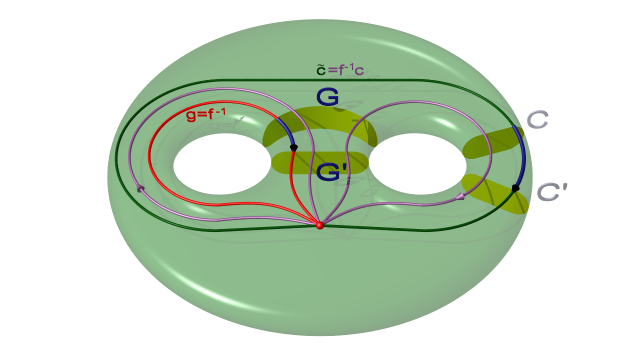
On obtient les relations $g\tilde c^{-1}g^{-1} \tilde cg^{-1}\tilde c^{-1}g^2$ et $\tilde c^{-1}g^{-1}\tilde c^2g^{-1}=\tilde c^{-1}g^{-1}\tilde c^3 \tilde c^{-1}g^{-1}$. Après conjugaison de la deuxième par $g \tilde c$ on obtient les relations :

$$\begin{array}{ll} \mbox{courbe blanche} & g\tilde c^{-1}g^{-1} \tilde cg^{-1}\tilde c^{-1}g^2 \\ \mbox{courbe bleu foncé} & \tilde c^3(g\tilde c)^{-2}. \end{array}$$

On peut ensuite utiliser la deuxième relation pour modifier la première. Cela correspond à compliquer le diagramme de manière à faire apparaître la courbe bleue comme « facteur » de la courbe blanche que l’on peut alors « simplifier » par ce facteur :

$$ \begin{split} g\tilde c^{-1}g^{-1} \tilde cg^{-1}\tilde c^{-1}g^2 & = g\tilde c^{-1}g^{-1} \tilde c g^{-1} (\tilde c^{-1} g^{-1} \tilde c \tilde c^{-1} g \tilde c ) \tilde c^{-1} g^2 \\ & = g\tilde c^{-1}g^{-1} \underbrace{\tilde c g^{-1} \tilde c^{-1} g^{-1} \tilde c}_{= 1} \tilde c^{-1} g \tilde c \tilde c^{-1} g^2 \end{split} $$

car la relation associée à la courbe bleu donne $\tilde cg^{-1}\tilde c^{-1}=\tilde c^{-1}g$. On peut donc remplacer la première relation par $g\tilde c^{-1}g^{-1}\tilde c^{-1}g^3$ qui, après conjugaison par $g^4$, est équivalente à $g^5(g\tilde c)^{-2}$. Dernière étape qui correspond à passer du diagramme :

$$ $$

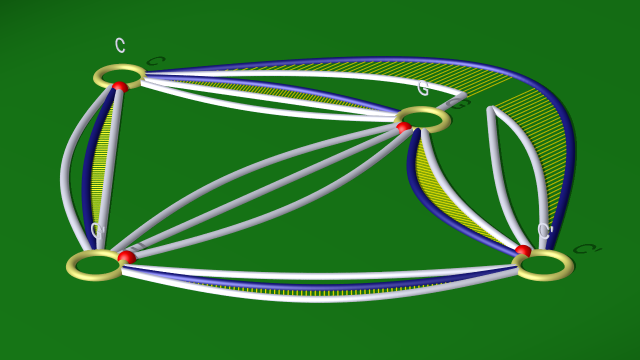
au diagramme

$$ $$

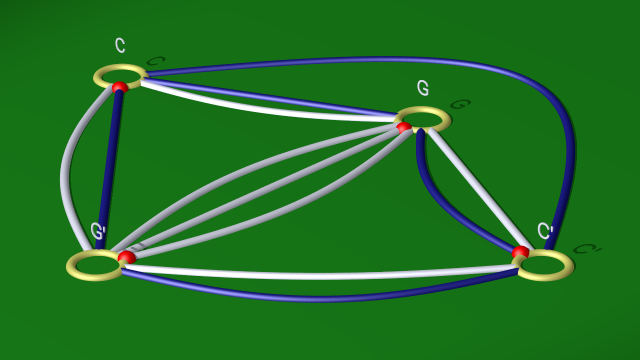
Il nous reste donc les relations

$$\begin{array}{ll} \mbox{courbe blanche} & g^5(g\tilde c)^{-2} \\ \mbox{courbe bleu foncé} & \tilde c^3(g\tilde c)^{-2}. \end{array}$$

Et la présentation du groupe $\pi_1(\Sigma)$ associée au scindement de Heegaard donné par Poincaré est donc

$$\langle \tilde c, g \mid g^5=\tilde c^3=(g\tilde c)^2 \rangle$$

Conséquences

Poincaré utilise cette présentation pour montrer que $\pi_1(\Sigma)$ n’est pas trivial. Pour vérifier cela on considère l’application $\phi$, de $\pi_1(\Sigma)$ vers le groupe alterné $A_5$ de degré $5$, définie sur les générateurs par

$$g\mapsto (1\,2\,3\,4\,5)\qquad \tilde c\mapsto (1\,4\,3).$$

Cette application définit un morphisme de groupes car $g\tilde c\mapsto(1\,2)(4\,5)$ [5]. Ce morphisme est surjectif : son image est un sous-groupe de $A_5$ engendré par un cycle d’ordre 5 et un cycle d’ordre 3. Son ordre est donc nécessairement égal à 15, 30 ou 60. Il ne peut pas être égal à 15 car les cycles $(1\,2\,3\,4\,5)$ et $(1\,4\,3)$ ne commutent pas. Et il ne peut pas être égal à non plus 30 car $A_5$, étant simple, ne peut avoir de sous-groupe d’ordre 30, i.e. d’indice 2, car un tel sous-groupe serait distingué. Le groupe $\pi_1(\Sigma)$ n’est donc pas trivial. C’est en outre un groupe parfait, c’est-à-dire qu’il coïncide avec son sous-groupe dérivé $[\pi_1 (\Sigma) , \pi_1(\Sigma )]$. En effet son abélianisé

$$\pi_1 (\Sigma ) / [\pi_1 (\Sigma) , \pi_1(\Sigma )]$$

est le groupe abélien engendré par deux éléments $a$ et $b$ soumis aux relations

$$5a = 3b = 2 a + 2b = 0.$$

D’où l’on tire facilement que $a=b=0$. Il découle alors du théorème de Hurewicz que $H_1 (\Sigma) = \{0\}$. Et la dualité de Poincaré implique que $\Sigma$ est une sphère d’homologie. Rappelons pour finir que l’on montre ici que le groupe $\pi_1(\Sigma)$ est fini d’ordre 120. En fait,

$$\langle a, b \; | \; a^5=b^3=(ab)^2 = 1 \rangle$$

est une présentation du groupe $A_5$. Pour le vérifier, une méthode consiste à écrire tous les mots possibles en $a$ et $b$ en tenant compte des relations, et de constater qu’on obtient 60 éléments différents. Une autre méthode consiste à voir $A_5$ comme le groupe maximal des isométries directes du dodécaèdre (ou de l’icosaèdre) régulier comme dans la première partie de ce cours filmé. Le noyau du morphisme $\phi$ est donc engendré par l’élément

$$g^5=\tilde c^3=(g\tilde c)^2$$

contenu dans le centre de $\pi_1 (\Sigma)$. Ce noyau est d’ordre 2 et $\pi_1(\Sigma)$ est donc isomorphe à un groupe d’ordre 120 extension centrale de $A_5$ par $\mathbb{Z} /2\mathbb{Z}$. [6]