Le diagramme de Heegaard de Poincaré

On a montré ici que la variété dodécaédrique de Poincaré (définie comme espace d’identification d’un dodécaèdre) possède un scindement de Heegaard de genre 2 décrit par le diagramme suivant.

$$ $$

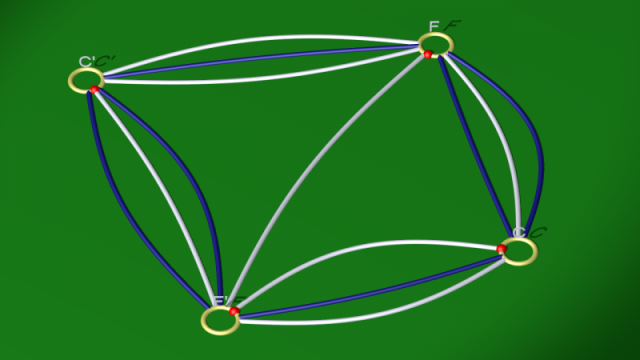
Ce diagramme n’est pas celui donné par Poincaré dans le cinquième complément, que voici [1] :

$$ $$

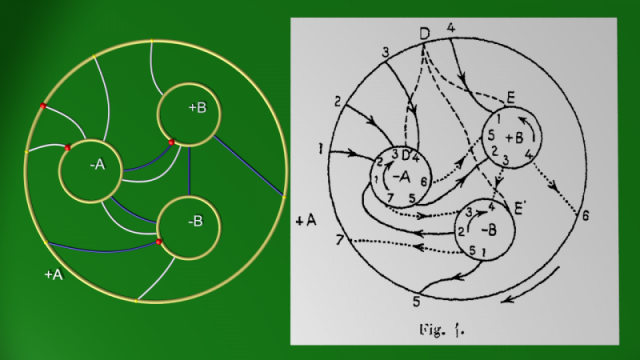
Le but de cet article est de démontrer qu’il lui est néanmoins équivalent, c’est-à-dire que la sphère d’homologie que construit Poincaré dans le cinquième complément et la variété dodécaédrique (construite à partir du dodécaèdre ou à partir du diagramme ci-dessus) sont une seule et même variété.

Pour démontrer cela, on part du premier diagramme de Heegaard ci-dessus et on fait subir à celui-ci une suite de manipulations élémentaires qui ne changent pas la topologie de la variété associée et qui aboutissent au diagramme de Poincaré, lui aussi de genre 2.

1. La première étape consiste à compliquer la décomposition en anses associée au diagramme ci-dessus en découpant la 0-anse en deux morceaux que l’on relie par une nouvelle 1-anse. On aboutit ainsi à une nouvelle décomposition en anses constituée de deux 0-anses, trois 1-anses et toujours deux 2-anses et une 3-anse.

$$ $$

On aboutit au diagramme « généralisé » suivant (où on spécifie encore l’identification des disques d’attachement à l’aide de marques rouges).

$$ $$

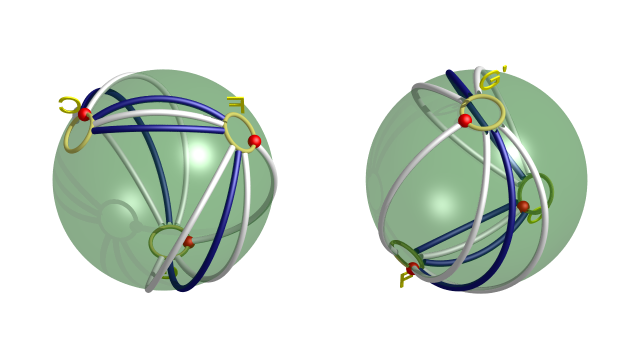
2. On revient à un diagramme de Heegaard « standard » en recollant les deux 0-anses selon les disques $F$ et $F'$ (en prenant garde à bien juxtaposer les courbes comme indiqué par les marques rouges sur les bords de ces deux disques).

$$ $$

On aboutit à la décomposition en anses suivante où la 0-anse a la forme de deux boules recollées selon un petit disque (ce qui donne bien un espace homéomorphe à une boule).

$$ $$

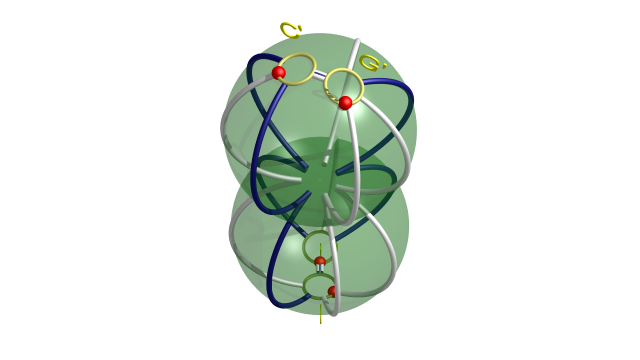
On peut déformer cette 0-anse pour lui donner la forme plus standard d’une boule.

$$ $$

On aboutit ainsi à la décomposition de Heegaard de genre 2 suivante :

$$ $$

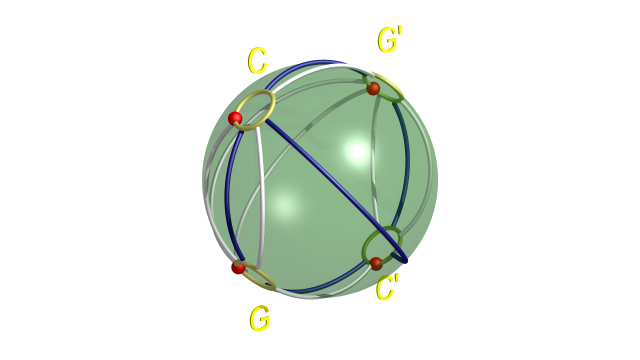
On revient à un diagramme plan dans la vidéo suivante.

$$ $$

Après ajout des marques rouges on aboutit finalement à un nouveau diagramme de Heegaard de genre 2 :

$$ $$

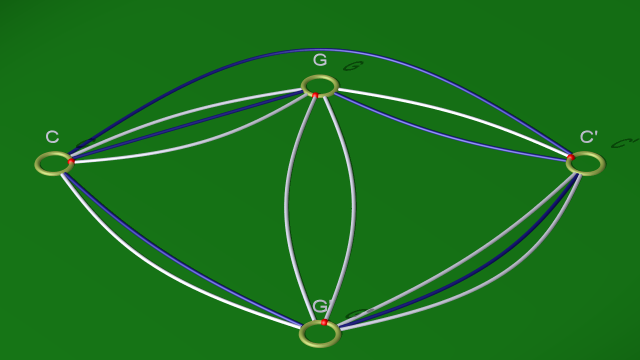
3. Maintenant, on complique dans un premier temps le diagramme ci-dessus pour faire apparaître la courbe bleue comme « facteur » de la courbe blanche que l’on peut alors « simplifier » par ce facteur.

$$ $$

Cette simplification consiste à passer du diagramme :

$$ $$

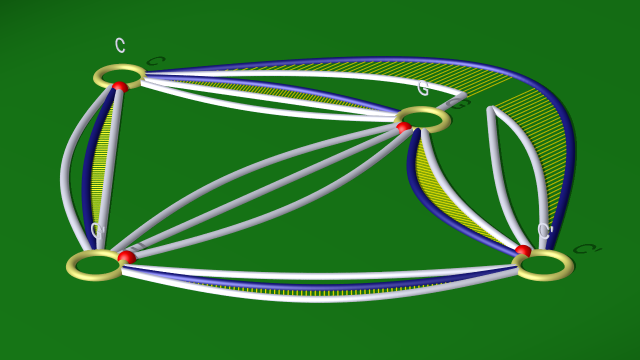
au diagramme

$$ $$

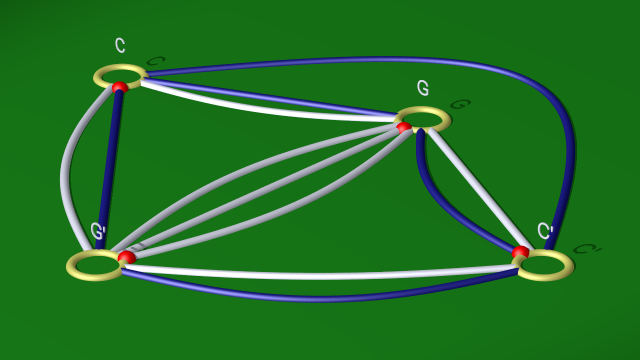
4. On change finalement le centre de la projection stéréographique [2] pour obtenir un nouveau diagramme :

$$ $$

Nouveau diagramme en lequel on reconnaît le diagramme de Poincaré :

$$ $$