
|
> Groupe fondamental > Groupe fondamental : exemples de calculs > Variétés sphériques Variétés sphériques |
On décrit ici les variétés de dimension $3$ qui sont des quotients de la sphère $\mathbb{S}^3$, et on explique que leur classification repose sur le théorème de géométrisation de Perelman.
Définition et caractérisation des variétés sphériques
Commençons par définir ce qu’on appelle variété sphérique.
Une variété compacte est dite sphérique si son revêtement universel est isomorphe à une sphère.
Les seules variétés sphériques de dimension $2$ sont la sphère et le plan projectif. Nous nous concentrons ici sur la dimension $3$.
Toute variété sphérique $M$ est de la forme $\Gamma \backslash \mathbb{S}^3$, où $\Gamma$ est un groupe d’homéomorphismes de $\mathbb{S}^3$ agissant proprement discontinûment sur $\mathbb{S}^3$. Comme la sphère de dimension $3$ est compacte, le groupe fondamental d’une variété sphérique est un groupe fini.

- Grigori Perelman en 1993
Réciproquement, si le groupe fondamental d’une variété compacte $M$ est fini, le revêtement universel de $M$ est une variété compacte simplement connexe. Peut-on en déduire que le revêtement universel de $M$ est une sphère ? C’est l’objet de la fameuse conjecture de Poincaré, qui a été démontrée en 2004 par Grigori Perelman.
En fait, Perelman a démontré un résultat plus fort : le théorème d’elliptisation. Ce théorème affirme qu’une variété compacte de dimension $3$ de groupe fondamental fini possède toujours une métrique sphérique et que par conséquent :
Toute variété sphérique de dimension $3$ est homéomorphe à un quotient de la sphère $\mathbb{S}^3$ par un groupe fini d’isométries.
Le groupe des isométries de $\mathbb{S}^3$ et ses sous-groupes finis
Pour classifier les variétés sphériques de dimension $3$, il reste donc à décrire les sous-groupes finis du groupes des isométries de $\mathbb{S}^3$ qui agissent librement sur $\mathbb{S}^3$. Pour simplifier les choses, restreignons-nous aux variétés orientables, et donc aux isométries de $\mathbb{S}^3$ qui préservent l’orientation, c’est-à-dire au groupe $\mathrm{SO}(4)$.
En utilisant les quaternions, on montre que $\mathbb{S}^3$ s’identifie au groupe $\mathrm{SU}(2)$, et que $\mathrm{SO}(4)$ s’identifie au groupe
$$\mathrm{SU}(2)\times \mathrm{SU}(2)/ \langle (- I_2 , -I_2) \rangle$$
dont l’action sur $\mathrm{SU}(2) \simeq \mathbb{S}^3$ est donnée par
$$(g,h) \cdot x = gxh^{-1}~.$$
Soit $\Gamma$ un sous-groupe fini de $\mathrm{SO}(4)$ agissant librement sur $\mathbb{S}^3$. Soit $\Gamma_0$ l’image réciproque de $\Gamma$ par le revêtement double de $\mathrm{SU}(2)\times \mathrm{SU}(2)$ sur $\mathrm{SO}(4)$, et notons $p_1$ et $p_2$ les restrictions à $\Gamma$ des projections de $\mathrm{SU}(2)\times \mathrm{SU}(2)$ sur le premier et second facteur.
Le noyau d’une des deux projections est cyclique.
Pour prouver cette proposition, nous admettrons le lemme suivant, qui découle de la classification des sous-groupes finis de $\mathrm{SU}(2)$ :
Tout sous-groupe fini non cyclique de $\mathrm{SU}(2)$ contient un élément d’ordre $4$.
Par l’absurde, supposons donc que les noyaux de $p_1$ et $p_2$ ne soient pas cycliques. Soit $(1,g_1)$ un élément du noyau de $p_1$ d’ordre $4$ et $(g_2, 1)$ un élément du noyau de $p_2$ d’ordre $4$. Les matrices $g_1$ et $g_2$ sont alors toutes deux conjuguées à la matrice
$$ \left(\begin{matrix} i & 0 \\ 0 & -i \end{matrix} \right)~.$$
Il existe donc $x \in \mathrm{SU}(2)$ tel que
$$g_2 = x\, g_1 x^{-1}~,$$
ce qui se réécrit
$$g_2 x g_1^{-1} = x~.$$
L’action de $(g_1,g_2) \in \Gamma_0$ sur $\mathrm{SU}(2) \simeq \mathbb{S}^3$ fixe donc le point $x$, ce qui contredit le fait que $\Gamma$ agit librement sur $\mathbb{S}^3$.
Il découle de cette proposition qu’il existe un morphisme $p$ de $\Gamma$ dans $\mathrm{SU}(2)/\langle -I_2\rangle \simeq \mathrm{SO}(3)$ dont le noyau est cyclique. La classification des variétés sphériques orientables de dimension $3$ se ramène donc essentiellement à classifier les sous-groupes finis de $\mathrm{SO}(3)$, ce qui permet de regrouper ces variétés en cinq catégories :
- Les variétés lenticulaires : ce sont les variétés dont le groupe fondamental est cyclique. On les décrit plus en détails ici.
Les variétés diédrales : ce sont celles dont le groupe fondamental est une extension cyclique d’un groupe diédral.
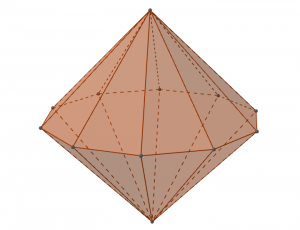
- Le groupe diédral $D_{10}$ est le groupe des isométries directes d’une double pyramide de base un décagone régulier.
- Les variétés tétraédriques : ce sont celles dont le groupe fondamental est une extension cyclique du groupe des isométries directes du tétraèdre régulier.
- Les variétés cubiques, dont le groupe fondamental est une extension cyclique du groupe des isométries directes du cube. Ce sont toutes des quotients de la variété hypercubique par un groupe cyclique.
- Les variétés dodécaédriques, dont le groupe fondamental est une extension cyclique du groupe des isométries directes du dodécaèdre. Ce sont toutes des quotients de la variété dodécaédrique de Poincaré par un groupe cyclique.
Notons pour finir que toutes ces variétés sont des fibrés de Seifert. Plus précisément, la variété $\Gamma \backslash \mathbb{S}^3$ est un fibré de Seifert au dessus de l’orbifold $p(\Gamma) \backslash \mathbb{S}^2$.
