Comme l’indice "1" le suggère, il existe des groupes $\pi_i(X)$ avec $i\geq 1$, mais Poincaré ne les connaissait pas !
On a expliqué ici comment définir le groupe fondamental $\pi_1(X,x_0)$ d’un espace topologique pointé $(X,x_0)$ comme l’ensemble des classes d’homotopies d’applications du cercle $\mathbb{S}^1$ dans $X$ basées en $x_0$. Cette définition peut se généraliser en considérant des classes d’homotopies d’applications continues des sphères $\mathbb{S}^2$, $\mathbb{S}^3$... dans $X$.
On commence par un court article général sur la notion d’homotopie :
Puis on définit les groupes d’homotopies :
Ces groupes d’homotopie complètent l’information donnée par le groupe fondamental. À titre d’exemple, si le groupe fondamental ne permet pas de distinguer topologiquement deux sphères ${\mathbb S}^i$ et ${\mathbb S}^j$ lorsque $2 \leq i < j$ (ce sont des espaces simplement connexes), les groupes d’homotopie supérieurs permettent eux de les distinguer.
Reste à comprendre comment calculer ces groupes d’homotopie supérieurs. C’est un problème difficile encore largement ouvert [1]. Un outil puissant est la Suite d’homotopie d’un espace fibré, qui relie les groupes d’homotopies de la base, de la fibre et de l’espace total d’une fibration. Cette suite exacte permet par exemple de montrer que le groupe $\pi_3({\mathbb S}^2)$ est isomorphe à ${\mathbb Z}$.
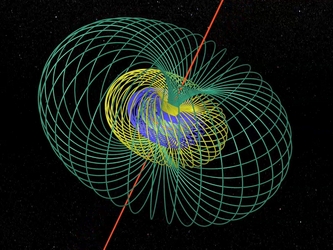
- La fibration de Hopf
Enfin, le théorème de Hurewicz établit (dans certains cas) un lien entre les groupes d’homologie et les groupes d’homotopie d’un espace topologique. En « degré » 1, le théorème était déjà bien connu de Poincaré ; il affirme que le premier groupe d’homologie d’un espace est l’abélianisé de son gorupe fondamental. Nous l’avons démontré ici. Nous présentons maintenant le cas général.
Signalons que nous avons choisi de présenter les éléments des groupes d’homotopies supérieurs d’un espace $X$ comme des classes d’homotopies d’applications des sphères $\mathbb{S}^2$, $\mathbb{S}^3$... dans $X$. On peut aussi les voir récursivement comme des lacets dans l’espace des lacets de $X$, puis des lacets dans l’espace des lacets de l’espace des lacets de $X$... C’est l’approche privilégiée par de nombreux livres modernes de topologie algébrique, avec laquelle le lecteur courageux devra se familiariser s’il ouvre par exemple le site internet Homotopy Type Theory.
[1] En général, on ne sait toujours pas calculer les groupes d’homotopie des sphères.