Le pinceau de cubiques de Hesse

Considérons dans $\mathbb{P}^2(\mathbb{C})$ les points suivants avec $j=e^{\frac{2i\pi}{3}}$ :

$$\begin{array}{ccc} p_0=[0,1,-1],& p_1=[0,1,-j],&p_2=[0,1,-j^2]\\ p_3=[1,0,-1],& p_4=[1,0,-j^2],&p_5=[1,0,-j]\\ p_6=[1,-1,0],& p_7=[1,-j,0],&p_8=[1,-j^2,0] \end{array}$$

Un peu d’algèbre linéaire montre que tout polynôme homogène d’ordre 3 dans les variables $x,y,z$ qui s’annule en chacun de ces points est nécessairement de la forme

$$Q_{a,b}=a(x^3+y^3+z^3)-3bxyz.$$

Faisant varier $[a,b]\in \mathbb{P}^1(\mathbb{C})$ le lieu $Q_{a,b}=0$ définit une famille de cubiques $C_{a,b}$ dans $\mathbb{P}^2(\mathbb{C})$ qui passent toutes par les points $p_0,\ldots,p_8$. On dit que cette famille est un « pinceau de cubiques ». Cette famille spécifique s’appelle le pinceau de Hesse, puisque c’est Otto Hesse qui en a étudié le premier les propriétés en 1844 [1].

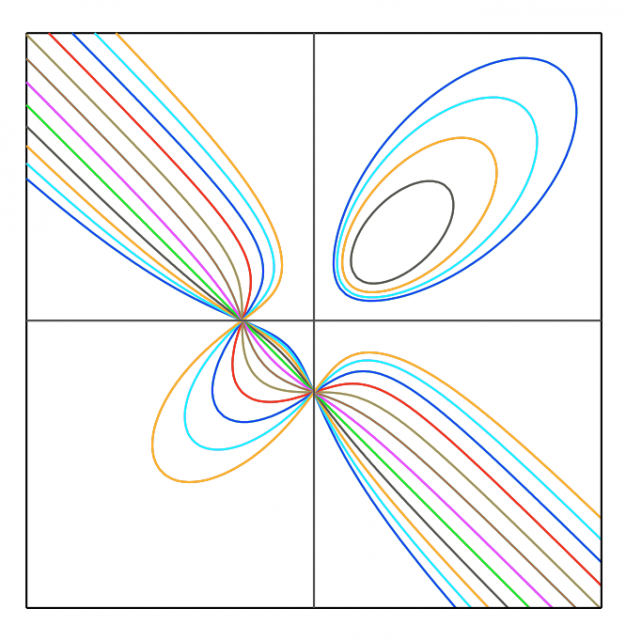
La partie réelle du pinceau de Hesse

L’application $p:\mathbb{P}^2(\mathbb{C})\to\mathbb{P}^1(\mathbb{C})$ définie par $p([x,y,z])=\frac{x^3+y^3+z^3}{3xyz}$ est indéterminée aux 9 points $p_0,\ldots,p_8$. Quitte à éclater $\mathbb{P}^2(\mathbb{C})$ en chacun de ces points, on obtient une nouvelle variété $\widetilde{\mathbb{P}}^2(\mathbb{C})$ et une application cette fois bien définie $p:\widetilde{\mathbb{P}}^2(\mathbb{C})\to\mathbb{P}^1(\mathbb{C})$. Il s’agit d’une fibration de Lefschetz : elle a quatre fibres singulières correspondant aux valeurs critiques de $p$ suivantes : $\infty,1,j,j^2$.

En effet, la résolution du système $Q_{a,b}=\partial_x Q_{a,b}=\partial_y Q_{a,b}=\partial_z Q_{a,b}=0$ donne $ax^2=byz,ay^2=bxz,az^2=bxy$. Si $a\ne 0$, en faisant le produit terme à terme, on a $a^3=b^3$ car $x,y,z$ ne peuvent pas s’annuler simultanément.

On se propose de trouver trois cycles évanescents correspondant aux trois valeurs critiques $1,j,j^2$ dans la fibre générique que l’on identifie à la cubique de Fermat

$$C_0=\{[x,y,z]\in\mathbb{P}^2(\mathbb{C}), x^3+y^3+z^3=0\}.$$

L’ensemble des solutions réelles de l’équation $x^3+y^3+z^3=0$ forme un cercle topologique. Pour s’en convaincre, on observe que si $z=0$ alors $x=-y$, ce qui correspond au point $[1,-1,0]$. Sinon, on se ramène à $z=1$ et on a alors $y=(-1-x^3)^{1/3}$.

Si on pose maintenant $p=\lambda\in [0,1]$ et $z=1$, on obtient $x^3+y^3+1-3\lambda xy =0$. Cette équation n’a qu’une solution réelle en $y$ ssi $-4\lambda^3x^3+(x^3+1)^2\ge0$ ce qui est bien le cas en distinguant les cas $x^3>0$ et $x^3<0$. On en déduit que le cercle initial se déforme continûment jusqu’aux points réels de l’équation

$$x^3+y^3+z^3-3xyz=0=(x+y+z)(x^2+y^2+z^2-xy-xz-yz)$$

Ce deuxième facteur ne s’annule pas sur $\mathbb{R}$ ainsi la partie réelle de la cubique dégénérée $p^{-1}(1)$ est une droite projective réelle d’équation $x+y+z=0$. Cette droite borde un disque dans la droite projective complexe associée. En résumé, la partie réelle de $C_0$ est un cycle qui s’évanouit en $\lambda=1$.

En remplaçant $z$ par $j^{\pm 1} z$ et $\lambda$ par $j^{\mp 1}\lambda$, on obtient la même équation et donc le même raisonnement s’applique. Cela nous dit que l’ensemble $\{[x,y,j^{\pm 1}z]\in C_0,(x,y,z)\in \mathbb{R}^3\}$ est un cycle évanescent correspondant aux valeurs critiques $j^{\pm 1}$. Notons $\gamma_{-1},\gamma_0,\gamma_1$ ces trois cycles dans $C_0$. On a :

$\gamma_0\cap\gamma_1=\gamma_0\cap\gamma_{-1}=\gamma_{-1}\cap\gamma_1=\{[x,y,0]\in C_0, (x,y)\in \mathbb{R}^2\}=[1,-1,0].$

Il s’agit donc des cycles $(t,0),(0,t)$ et $(t,t)$ dans $\mathbb{R}^2/\mathbb{Z}^2$ avec $t\in [0,1]$. En particulier, ils engendrent bien le groupe fondamental de $C_0$.

La description du groupe fondamental des fibrations de Lefschetz obtenue dans cet article montre ainsi que le groupe fondamental de $\tilde{\mathbb{P}}^2(\mathbb{C})$ est trivial. Ceci découle aussi de la construction de $\tilde{\mathbb{P}}^2(\mathbb{C})$ comme éclaté en 9 points de $\mathbb{P}^2(\mathbb{C})$ : en effet, $\mathbb{P}^2(\mathbb{C})$ est simplement connexe et l’éclatement ne modifie pas le groupe fondamental.

Le groupe des transformations projectives qui préservent le pinceau de Hesse est le groupe (d’ordre 216) des transformations affines de déterminant 1 du plan sur $\mathbb{F}_3$. Il a été découvert par Jordan en 1878 qui l’a appelé le groupe de Hesse. Pour plus d’information sur cette famille de cubiques, on renvoie à la référence suivante :

Michela Artebani and Igor Dolgachev, The Hesse pencil of plane cubic curves, Enseign. Math. (2) 55 (2009), no. 3-4, 235-273.