
|
> Homologie > Homologie singulière > Degré d’une application Degré d’une application |
Le but de cet article est de définir le degré d’une application continue d’une variété connexe fermée dans elle-même.
Si $X$ est une variété fermée (i.e. compacte sans bord) connexe orientable de dimension $n$, alors le groupe d’homologie singulière de degré maximal $H_n(X,\mathbb{Z})$ est isomorphe à $\mathbb{Z}$.
À vrai dire, nous n’avons pas encore les outils pour démonter ce fait. Cependant, nous avons en vu ici une preuve dans le cas particulier où $X$ est la sphère $\mathbb{S}^n$. Par ailleurs, le fait est facile à démontrer si on remplace l’homologie singulière par l’homologie simpliciale : la preuve donnée ici se généralise sans difficulté au cas d’une variété de dimension arbitraire.
Dès lors, nos lecteurs ont trois possibilités.
- Nous faire confiance (nous déconseillons formellement cette attitude !).
- Aller lire ici pourquoi les groupes d’homologie singulière sont isomorphe aux groupes d’homologie simpliciaux.
- Lire la suite de cet article en remplaçant partout $X$ par la sphère $\mathbb{S}^n$.
Soit $X$ une variété fermée connexe de dimension $n$, et $f:X\to X$ une application continue. D’après le fait ci-dessus, le groupe d’homologie $H_n(X)$ est isomorphe à $\mathbb{Z}$ ; notons $\tau$ l’un des deux générateurs de ce groupe [1]. On a alors $f_*(\tau)=\mathrm{deg}(f).\tau$ où $\mathrm{deg}(f)$ est un entier, qui ne dépend pas du choix de $\tau$. Cet entier s’appelle le degré de l’application $f$.
- Le degré d’une application ne dépend que sa classe d’homotopie.
- Le degré est multiplicatif :
$$\mathrm{deg}(g\circ f) = \mathrm{deg}(g)\cdot \mathrm{deg}(f)\mbox{ et }\mathrm{deg}(id)=1.$$
La première propriété est une conséquence de l’invariance de l’homologie par homotopie : deux applications homotopes induisent le même morphisme en homologie. La seconde découle directement de la définition du degré.
Exemple. On voit $\mathbb{S}^1$ comme le cercle unité de $\mathbb C$. Alors l’application $z\mapsto z^2$ est de degré $2$. En effet, considérons le simplexe $\sigma$ défini par $\sigma(t)=e^{2i\pi t}$.
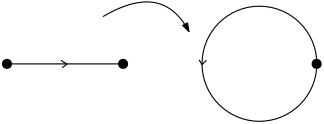
Alors $\sigma$ engendre $H_1(\mathbb{S}^1)$ et $f_*(\sigma)=2\sigma$ (attention, si on revient à la définition de l’homologie singulière, ce résultat est un peu moins évident qu’il n’y parait).
Voici un autre exemple sous forme d’exercice.
- On voit la sphère $\mathbb{S}^n$ comme la réunion de deux $n$-simplexes $\Delta_n$ et $\Delta_n '$ identifiés le long de leur bords de manière évidente et en préservant l’ordre des sommets. Montrer que $\Delta_n - \Delta_n '$ représente un générateur de $H_n (\mathbb{S}^n)$.
- Montrer que le degré $\mathrm{deg}(-\mathrm{id})$ de l’application antipodale $z\mapsto -z$ sur la sphère $\mathbb{S}^n$ est $(-1)^{n+1}$. En déduire que l’application antipodale n’est pas homotope à l’identité.
On peut calculer le degré d’une application différentiable sans passer par son action en homologie. L’exercice (pas facile) suivant explique comment.
Soit $X$ une variété fermée connexe orientée et $f:X\to X$ une application différentiable. Si $y$ est une valeur régulière de $f$, alors $f^{-1}(\{y\}$ est une variété compacte de dimension $0$ (voir ici, c’est-à-dire une collection finie de points $\{x_1,\dots,x_p\}$. À chaque $x_i$, on affecte le poids $\mathrm{deg}_{x_i}(f)=+1$ ou $-1$ selon que $Df(x_i)$ envoie une base directe de $T_{x_i}$ (pour l’orientation de $X$) sur un base directe de $Y$ ou pas.
- Montrer que l’entier $\sum_{x_i\in f^{-1}(y)} \mathrm{deg}_{x_i}(f)$ ne dépend pas de la valeur régulière $y$.
- Montrer que cet entier n’est autre que le degré de $f$.
Les lecteurs qui « sècheraient » sur cet exercice en trouveront une solution (rédigée dans le cas particulier où $X=\mathbb{S}^1$, mais que l’on peut généraliser à une variété quelconque) ici. On pourra par ailleurs consulter le chapitre 3 du livre de topologie différentielle de Guillemin et Pollack, où le degré d’une application est défini dans l’esprit de l’exercice ci-dessus.
V. Guillemin and A. Pollack. Differential Topology. AMS, 2010.
[1] On dit que $\tau$ est une classe fondamentale de $f$.
