Homologie des surfaces non-orientables

Dans cet article, on décrit le second groupe d’homologie des surfaces non-orientables. On observe que si $\Sigma$ est une surface fermée non-orientable, alors $H_2(\Sigma, \mathbb{Z}) = 0$ alors que $H_2(\Sigma,\mathbb{Z}/2\mathbb{Z}) \simeq \mathbb{Z}/2\mathbb{Z}$. Cela illustre un aspect non-trivial du théorème des coefficients universels.

Classe fondamentale des surfaces non-orientables

Soit $\Sigma$ une surface connexe fermée. Nous allons calculer le second groupe d’homologie simpliciale de $\Sigma$. Fixons donc une triangulation de $\Sigma$. Choisissons une orientation pour chaque face de la triangulation, et notons $(F_i)_{i\in I}$ les faces ainsi orientées. Notons également $(A_j)_{j\in J}$ les arêtes de cette triangulation.

Cherchons maintenant à construire un cycle de la forme $\sum_{i\in I} a_i F_i$, où $a_i\in \mathbb{Z}$. Quitte à changer l’orientation de certains de $F_i$, on peut supposer que les $a_i$ sont tous positifs. Ecrivons

$$ \partial \sum_{i\in I} a_i F_i = \sum_{j\in J} b_j A_j~.$$

Comme chaque arête $A_j$ borde exactement deux faces $F_{j_1}$ et $F_{j_2}$, on obtient que $b_j$ est nul si et seulement si $a_{j_1} = a_{j_2}$ et les orientations de $F_{j_1}$ et $F_{j_2}$ sont compatibles.

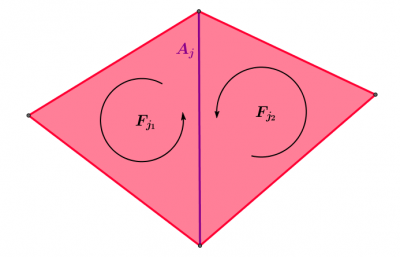
Pour que la contribution à $A_j$ dans $\partial \sum a_i F_i$ soit nulle, il faut que $a_{j_1}$ soit égal à $a_{j_2}$ et que les orientations de $F_{j_1}$ et $F_{j_2}$ soient compatibles.

Par conséquent, si $\sum_{i\in I} a_i F_i$ est un cycle, alors tous les $a_i$ sont égaux, et les orientations des $F_i$ fournissent une orientation globale de la surface $\Sigma$. Comme, par ailleurs, aucun $2$-cycle ne peut être le bord d’une $3$-chaîne (puisqu’il n’y a pas de $3$-chaîne), on peut conclure :

Lorsque $\Sigma$ est orientable, le choix d’un générateur de $H_2(\Sigma, \mathbb{Z})$ est équivalent au choix d’une orientation. Le générateur choisi est appelé classe fondamentale de la surface orientée.

Contrairement à l’homologie entière, l’homologie à coefficients dans $\mathbb{Z}/2\mathbb{Z}$ "oublie" l’orientation, puisque $-1 = 1$ modulo $2$. Par conséquent, que la surface $\Sigma$ soit orientable ou non, $\sum_{i\in I} F_i$ est un $2$-cycle modulo $2$. On en déduit :

On peut donc définir la classe fondamentale d’une surface non-orientable, si on se restreint à la cohomologie à coefficients dans $ \mathbb{Z}/2\mathbb{Z}$. Cela peut parfois être utile, par exemple pour prouver que les surfaces fermées plongées dans l’espace sont orientables.

Le théorème des coefficients universels

On constate donc que, pour une surface non-orientable, le second groupe d’homologie à coefficients dans $\mathbb{Z}/2\mathbb{Z}$ n’est pas simplement la réduction modulo $2$ du second groupe d’homologie à coefficients entiers. C’est en fait une conséquence du théorème des coefficients universels, qui permet de calculer l’homologie à coefficients dans un groupe abélien quelconque à partir de l’homologie à coefficients entiers.

Dans le cas qui nous intéresse, le théorème des coefficients universels affirme qu’on a la suite exacte suivante :

$$0 \to H_2(\Sigma,\mathbb{Z})\otimes \mathbb{Z}/2\mathbb{Z} \to H_2(\Sigma, \mathbb{Z}/2\mathbb{Z})\to \mathrm{Tor}\left(H_1(\Sigma), \mathbb{Z}/2\mathbb{Z}\right)~,$$

où $\mathrm{Tor}\left(H_1(\Sigma), \mathbb{Z}/2\mathbb{Z}\right)$ désigne la réduction modulo $2$ de la partie de torsion de $H_1(\Sigma, \mathbb{Z})$. Plus précisément, si

$$H_1(\Sigma, \mathbb{Z})\simeq \mathbb{Z}^k \oplus \bigoplus_{i=1}^l \mathbb{Z}/n_i \mathbb{Z}~,$$

alors

$$\mathrm{Tor}\left(H_1(\Sigma), \mathbb{Z}/2\mathbb{Z}\right) \simeq \bigoplus_{i \mid n_i \textrm{ pair}} \mathbb{Z}/2\mathbb{Z}~.$$

Soit $\Sigma$ une surface non-orientable. Supposons que $\mathrm{Tor}\left(H_1(\Sigma), \mathbb{Z}/2\mathbb{Z}\right)$ soit nul. Le théorème des coefficients universels donnerait alors

$$H_2(\Sigma,\mathbb{Z}/2\mathbb{Z}) \simeq H_2(\Sigma,\mathbb{Z}) \otimes \mathbb{Z}/2\mathbb{Z} = 0~.$$

Puisque $H_2(\Sigma,\mathbb{Z}) = 0$, on a, d’après le théorème des coefficients universels :

$$\mathrm{Tor}\left(H_1(\Sigma), \mathbb{Z}/2\mathbb{Z}\right) \simeq H_2(\Sigma,\mathbb{Z}/2\mathbb{Z}) \simeq \mathbb{Z}/2\mathbb{Z}~.$$

Autrement dit, $H_1(\Sigma,\mathbb{Z})$ doit contenir un facteur $\mathbb{Z}/n \mathbb{Z}$ avec $n$ pair. On peut le vérifier : on a vu par exemple dans l’introduction à l’homologie polyédrale que

$$H_1(\textrm{plan projectif},\mathbb{Z}) \simeq \mathbb{Z}/2\mathbb{Z}$$

et que

$$H_1(\textrm{bouteille de Klein},\mathbb{Z}) \simeq \mathbb{Z} \oplus \mathbb{Z}/2\mathbb{Z}~.$$