Les premières surfaces : la sphère, le cylindre, le tore

La sphère

La sphère unité.

La sphère unité $\mathbb{S}^2$ est une surface bien connue : c’est l’ensemble des points de $\mathbb{R}^3$ à distance $1$ de l’origine. Autrement dit, c’est la surface algébrique d’équation

$$x^2+y^2 +z^2 = 1~.$$

Toutefois, la topologie ne s’intéresse qu’aux propriétés qui sont invariantes par homéomorphisme. On appelle donc sphère toute surface qui est homéomorphe à la sphère unité $\mathbb{S}^2$. De ce point de vue, un ballon de rugby est une sphère, même s’il n’a pas la même forme géométrique qu’un ballon de foot.

Un ballon de football et un ballon de rugby sont tous deux des sphères topologiques.

De même, la surface d’un cube est homéomorphe à une sphère, comme on le voit dans la vidéo qui suit. Cette vidéo présente également trois autres façons de construire la sphère : en recollant deux disques le long de leur bord, en repliant sur eux-mêmes les côtés d’un carré, ou encore en compactifiant le plan en ajoutant un "point à l’infini".

Le cylindre

Voilà un cylindre.

Voici une autre surface assez simple : le cylindre. On peut également le "mettre en équations" et le présenter comme l’ensemble des points de $\mathbb{R}^3$ qui satisfont

$$x^2+y^2 = 1$$

et

$$-1 \leq z\leq 1~.$$

C’est une surface à bord dont le bord est formé de deux cercles.

Insistons encore une fois sur le fait que la topologie s’intéresse à des objets définis "à déformation près". On appelle donc cylindre n’importe quelle surface homéomorphe au cylindre dont les équations sont données ci-dessus. Ainsi, le tuyau d’un cor ou la cheminée d’une centrale électrique (les experts reconnaîtront peut-être un hyperboloïde à une nappe) sont des cylindres topologiques.

Un cor ou une cheminée de centrale électrique sont homéomorphes à des cylindres.

Pour fabriquer un cylindre, il suffit de rouler une feuille de papier. Inversement, on peut imaginer dérouler un cylindre en une bande de papier infinie (mais infiniment fine), comme expliqué sur la vidéo qui suit. Le cylindre peut alors être décrit comme le quotient de cette bande infinie par une translation.

Le tore

Lorsqu’on tord un cylindre pour recoller ensemble ses deux bords, on obtient un tore.

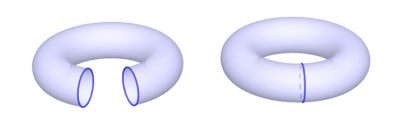
En recollant les deux bords d’un cylindre, on obtient un tore.

Si on recolle les côtés de ce carré en suivant les flèches, on obtient un tore.

On peut aussi présenter le tore comme le carré dessiné ci-contre, dont on a recollé le côté gauche sur le côté droit, et le côté bas sur le côté haut. Par exemple, dans le jeu vidéo Pacman, lorsque le personnage sort de l’écran par la droite il réapparaît à gauche, et lorsqu’il sort par le haut il réapparaît en bas. Pacman vit donc sur un tore !

Enfin, on peut identifier le tore au quotient du plan $\mathbb{R}^2$ par l’action de $\mathbb{Z}^2$ par translation. La vidéo qui suit illustre le lien entre ces différents points de vue.