Quelques surfaces non-orientables

Orientabilité d’une surface

Une surface plongée dans l’espace est orientable si on peut définir les deux "côtés" de la surface. Elle est non-orientable si elle n’a qu’un seul côté. Poincaré parle d’ailleurs de surface bilatère ou unilatère (du latin latus, lateris qui signifie "côté").

Le premier exemple de surface non-orientable (la "variété unilatère que tout le monde connaît" d’après Poincaré), c’est le célèbre ruban de Möbius, dont Escher a réalisé quelques belles gravures.

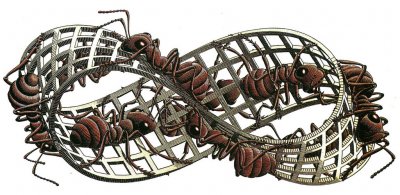
Des Fourmis sur un ruban de Möbius (dessin d’Escher).

On voit sur ce dessin qu’une fourmi qui se promène d’un côté du ruban finit par se retrouver de l’autre côté sans s’en rendre compte. C’est d’ailleurs à cause de cette propriété que le ruban de Möbius a donné son nom à un sympathique film d’espionnage (voir la bande annonce à la minute 01:50).

Cette définition de l’orientabilité n’est cependant pas tout-à-fait satisfaisante, puisqu’elle suppose que la surface est plongée dans l’espace. On peut donner une définition plus intrinsèque : Considérons une petite flèche qui se déplace sur une surface $S$. On dit que $S$ est orientable si on peut définir de façon consistante la gauche et la droite de la flèche. On trouvera une définition rigoureuse (mais beaucoup plus formelle) dans le cours moderne.

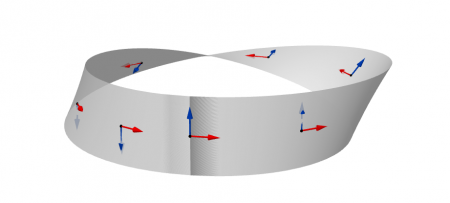
Lorsque la flèche rouge se déplace le long du ruban, la flèche bleue, qui initialement pointait vers la gauche, revient en pointant vers la droite. Le ruban de Möbius n’est donc pas orientable.

Le ruban de Möbius n’est pas la seule surface non-orientable. Nous présentons dans cet article deux autres surfaces non-orientables : le plan projectif et la bouteille de Klein.

Le plan projectif

Le plan projectif $\mathbb{R}\mathrm{P}^2$, bien connu des mathématiciens depuis le XVIIe siècle et les travaux de Desargues, est l’ensemble droites de $\mathbb{R}^3$ passant par l’origine.

Comme chacune de ces droites intersecte la sphère

$$\mathbb{S}^2 = \{(x,y,z)\in\mathbb{R}^3 \mid x^2+y^2+z^2=1\}$$

en deux points symétriques par rapport à l’origine, le plan projectif peut être vu comme le quotient de $\mathbb{S}^2$ par l’involution

$$(x,y,z) \mapsto (-x,-y,-z)~.$$

Comme cette involution renverse l’orientation de la sphère, le plan projectif n’est pas orientable. C’est le premier exemple de surface fermée (i.e. compacte sans bord) non-orientable.

La vidéo qui suit illustre cette définition et explique que, lorsqu’on perce un trou dans le plan projectif, on obtient un ruban de Möbius.

On peut essayer de représenter le plan projectif comme une surface dans l’espace, mais il y a un prix à payer : il faut autoriser la surface à s’auto-intersecter. En effet, il est impossible de plonger une surface compacte sans bord non-orientable dans l’espace.

Pourquoi ?

Intuitivement, on a envie de dire que toute surface fermée plongée dans l’espace a un intérieur et un extérieur, et qu’on peut donc définir les deux côtés de la surface. Mais ce fait n’a rien d’évident. Nous en donnons une preuve dans l’article intitulé "Les Surfaces plongées dans l’espace sont orientables".

En revanche, on peut construire des immersions du plan projectif dans l’espace. La vidéo suivante présente une première immersion, qui donne une surface (singulière) appelée cross-cap :

La vidéo suivante présente une autre immersion du plan projectif appelée surface de Boy :

On peut voir une autre construction de la surface de Boy dans cette vidéo de Dusan Zivaljevic.

$$ $$

La bouteille de Klein

Le bord d’un ruban de Möbius est un cercle. Si l’on prend deux rubans de Möbius et qu’on les recolle le long de leur bord, on voit apparaître une nouvelle surface fermée non-orientable : la bouteille de Klein.

La vidéo suivante illustre cette construction. Comme le plan projectif, la bouteille de Klein ne peut pas être plongée dans l’espace, puisqu’elle n’est pas orientable. En revanche, on obtient une jolie immersion qui ressemble à une bouteille étrange, dont le goulot pénètre à l’intérieur du corps de la bouteille.

Il existe de nombreux autres points de vue sur la bouteille de Klein. On peut par exemple la présenter comme le quotient du plan $\mathbb{R}^2$ par le groupe engendré par les deux transformations affines suivantes :

$$(x,y) \mapsto (x+1,-y)~,$$

$$(x,y) \mapsto (x,y+1)~.$$

On peut aussi la décrire comme le carré dessiné ci-dessous, où on a recollé les côtés jaunes ensemble et les côtés verts ensemble en suivant le sens indiqué par les flèches.

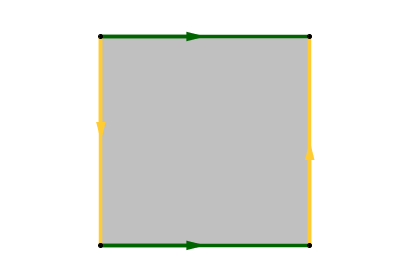
Si on recolle les bords de se carré en suivant les flèches, on obtient une bouteille de Klein.

La vidéo qui suit illustre ces deux points de vue et aboutit à une nouvelle immersion de la bouteille de Klein dans l’espace.

Revêtement d’orientation

De même que le plan projectif est un quotient de la sphère, la bouteille de Klein est le quotient du tore par une involution qui renverse l’orientation. Plus précisément, notons $\mathbb{U}^1$ le cercle unité dans $\mathbb{C}$ et identifions le tore $\mathbb{T}^2$ à $\mathbb{U}^1 \times \mathbb{U}^1$. Alors le quotient de $\mathbb{T}^2$ par l’involution

$$i: \left(e^{i\theta}, e^{i\phi}\right) \mapsto \left(e^{-i\theta}, -e^{i\phi}\right)$$

est homéomorphe à la bouteille de Klein.

Plus généralement, toute surface non-orientable $\Sigma$ est le quotient d’une surface orientable $\hat{\Sigma}$, appelée revêtement d’orientation de $\Sigma$, par une involution $i:\hat{\Sigma} \to \hat{\Sigma}$ qui renverse l’orientation. La construction générale du revêtement d’orientation d’une variété est présentée dans le cours moderne.

Il n’est pas rare que, pour prouver un résultat général sur des variétés, on commence par se ramener au cas des variétés orientables en "passant au revêtement d’orientation". En effet, il est parfois plus facile de travailler avec des variétés orientables. Par exemple, le théorème de dualité de Poincaré n’est vrai que pour des variétés compactes orientables.