
|
> Homologie > Homologie singulière > Homologie relative Homologie relative |
De nombreux espaces topologiques sont obtenus en recollant selon des sous-espaces des espaces topologiques « plus simples ». Il est alors naturel de considérer l’homologie d’un espace relativement à un sous-espace. Les cycles (qui généralisent les « sous-variétés fermées ») sont remplacés par les chaînes dont le bord est contenu dans le sous-espace. On peut ici se placer au choix dans la catégorie des complexes simpliciaux/polyèdraux ou des espaces topologiques. Selon les cas la théorie homologique considérée est donc l’homologie polyédrale/simpliciale ou l’homologie singulière. L’homologie relative est utilisée ici pour faire de premiers calculs non triviaux en homologie singulière.
Chaînes relatives et leurs homologies
Une paire est un couple $(X,A)$ où $A$ est un sous-espace de $X$. On a alors des inclusions $C_i (A) \subset C_i (X)$ et on pose :
$$C_i (X,A) = C_i (X) / C_i (A).$$
Les $C_i (X,A)$ forment encore un complexe de chaîne, appelé complexe de chaînes relatives de $(X,A)$. En effet, pour définir l’application bord on remarque que si $\alpha \in C_i (X)$ alors l’image de $\partial \alpha$ dans le quotient $C_{i-1} (X ) / C_{i-1} (A)$ ne dépend que de la classe de $\alpha$ modulo $C_i (A)$.
Les groupes d’homologie relative d’une paire $(X,A)$ sont les groupes d’homologie du complexe de chaînes relatives $C_{\bullet} (X,A)$ ; on les note $H_i (X,A)$.
Voici deux représentants d’une même chaîne dans $C_1(X,A)$
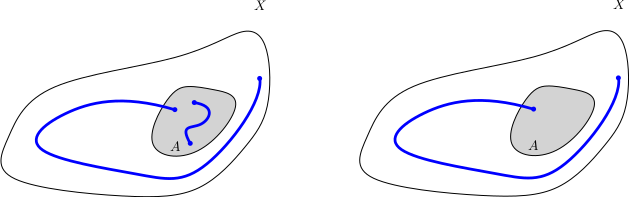
et un cycle de $C_1(X,A)$.
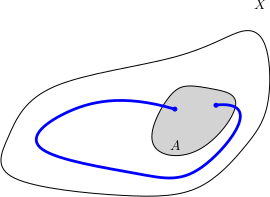
Dans le cas de l’homologie relative singulière, il n’est pas dur de vérifier qu’une application continue $f:(X,A)\to (Y,B)$ entre paires induit aussi un morphisme de complexe de chaînes $f_*:C_\bullet(X,A)\to C_{\bullet}(Y,B)$ (par simple passage au quotient) et donc un morphisme --- encore et toujours noté $f_*$ --- entre les groupes d’homologie relative.
On obtient trois complexes :
$$\begin{CD} @>>> C_i (A) @>>> C_{i-1} (A) @>>> \\ @. @VVV @VVV \\ @>>> C_i (X) @>>> C_{i-1} (X) @>>> \\ @. @VVV @VVV \\ @>>> C_i (X,A) @>>> C_{i-1} (X,A) @>>> \end{CD} $$
où l’application $C_i (A) \to C_i (X)$ est induite par l’inclusion et l’application $ C_i (X) \to C_i (X,A)$ est induite par la projection. Chaque suite verticale
$$C_i (A) \to C_i (X) \to C_i (X,A)$$
forme alors une suite exacte courte, c’est-à-dire qu’elle s’étend en une suite exacte
$$0 \to C_i (A) \to C_i (X) \to C_i (X,A) \to 0.$$
Pour toute paire $(X,A)$, il existe pour tout $i$ dans $\mathbb{Z}$ un morphisme
$$\delta : H_i (X,A) \to H_{i-1} (A)$$
tels que la suite infinie
$$ \ldots \to H_i (A) \to H_i (X) \to H_i (X,A) \stackrel{\delta}{\to} H_{i-1} (A) \to \ldots \to H_0 (X) \to H_0 (X,A) \to 0 $$
soit exacte.
Les applications $H_i (A) \to H_i (X)$ et $H_i (X) \to H_i (X,A)$ sont les applications naturelles, induites par les morphismes de complexes $C_i (A) \to C_i (X)$ et $C_i (X) \to C_i (X,A)$ [1].
Soit $x$ un point de $X$. La suite exacte longue précédente permet de prouver que les groupes $H_i (X, \{x \})$ et $H_i (X)$ sont isomorphes pour tout $i>0$. En degré $0$, si $(X_\alpha)$ est la famille des composantes connexes par arcs de $X$, on a
$$H_0 (X) = \bigoplus_{\alpha}\mathbb{Z} \text{ et } H_0 (X , \{x\}) = \bigoplus_{\alpha\neq\alpha_0}\mathbb{Z}$$
où $x\in X_{\alpha_0}$. En effet, pour $i>2$, on obtient
$$0\to H_i(X)\to H_i(X,\{x\})\to 0$$
et le résultat est immédiat. En outre, l’application $H_0(\{x\})\to H_0(X)$ est injective, il vient donc
$$0\to H_1(X)\to H_1(X,\{x\})\stackrel{0}{\to} \mathbb Z \to H_0(X) \to H_0(X,\{x\}) \to 0$$
ce qui permet de conclure.
Les groupes $H_i (X , \{x\})$ sont appelés groupes d’homologie réduite ; on les note $\widetilde{H}_i (X)$.
Décrivons comment construire le morphisme « de bord » $\delta$ dans la suite exacte longue d’homologie relative. Un cycle dans $C_i (X,A)$ peut être représenté par une chaîne $\alpha \in C_i (X)$ dont le bord $\partial \alpha$ est contenu dans $C_{i-1} (A)$. La classe de $\partial \alpha$ dans $H_{i-1} (A)$ ne dépend que de la classe de $\alpha$ modulo $C_i (A)$. On définit donc $\delta$ comme étant le morphisme qui associe à chaque cycle dans $C_i (X,A)$ la classe d’homologie de son bord dans $C_{i-i} (A)$.
La démonstration du théorème est en fait purement algébrique ; elle résulte de la proposition suivante qui signe l’acte de naissance de l’algèbre homologique et qui est démontrée ici.
Si $C \to C' \to C''$ est une suite exacte courte de complexes, il existe une suite exacte longue
$$ \ldots \to H_i (C) \to H_i (C') \to H_i (C'') \to H_{i-1} (C) \to \ldots \to H_0 (C' )\to H_0(C'') \to 0. $$
des groupes d’homologie de ces complexes.
En outre, si $(X,A)$ et $(Y,B)$ sont deux paires telles qu’il existe un diagramme commutatif
$$ \xymatrix{ C(A) \ar@{^{(}->}[r] \ar[d]^{\alpha} & C(X) \ar@{->>}[r] \ar[d]^{\beta} & C(X,A) \ar[d]^{\gamma} \\ C(B) \ar@{^{(}->}[r] & C(Y) \ar@{->>}[r] & C(Y,B)} $$
induit, par exemple, par une application $f : (X,A)\to(Y,B)$ alors le diagramme de la suite exacte longue induit en homologie est lui aussi commutatif.
$$ \begin{CD} \dots H_{i} (A) @>>> H_i (X) @>>> H_i (X,A) @>>> H_{i-1} (A) \ldots \\ @VVV @VVV @VVV @VVV \\ \dots H_{i} (B) @>>> H_i (Y) @>>> H_i (Y,B ) @>>> H_{i-1} (B) \ldots \end{CD} $$
Là encore, le résultat découle d’une propriété purement algébrique.
Soit
$$ \xymatrix{ C \ar@{^{(}->}[r] \ar[d]^{\alpha} & C' \ar@{->>}[r] \ar[d]^{\beta} & C'' \ar[d]^{\gamma} \\ D \ar@{^{(}->}[r] & D' \ar@{->>}[r] & D''} $$
un diagramme commutatif de complexes de chaînes dont les lignes sont des suites exactes (courtes). Alors, le diagramme de suites exactes longues induit en homologie
$$ \begin{CD} \dots H_{i} (C) @>>> H_i (C') @>>> H_i (C'') @>>> H_{i-1} (C) \ldots \\ @VVV @VVV @VVV @VVV \\ \dots H_{i} (D) @>>> H_i (D') @>>> H_i (D'' ) @>>> H_{i-1} (D) \ldots \end{CD} $$
est commutatif.
[1] On prendra toutefois garde au fait qu’une inclusion de complexes n’induit pas nécessairement une application injective en homologie : l’image d’un cycle non homologue à $0$ dans le petit complexe peut être homologue à $0$ dans le grand.
