Commentaires sur le §10 de l’Analysis Situs (Représentation géométrique)

En généralisant une pratique bien acceptée — et largement utilisée par Klein et Poincaré — dans le cas des surfaces, Poincaré propose (sans démonstration :-)) une méthode générale de construction de variétés.

Poincaré fait par ailleurs remarquer que la variété obtenue par recollement des faces de $P$ ne dépend, à homéomorphisme près, que de la combinatoire du recollement. Cela peut se déduire de lemmes de recollements.

Commentaires sur la démonstration de la proposition.

La proposition ci-dessus implique, et est impliquée par, le fait que la variété $M$ possède une cellulation — et même une triangulation — lisse. On note $P/ \iota$ la décomposition cellulaire de $M$ associée à la donnée $(P, \iota)$.

$$ $$

Commentaires sur le lien entre la proposition et la classification des surfaces.

La proposition ci-dessus — ou la triangulabilité des surfaces — permet de classifier toutes les surfaces compactes à homéomorphisme près, voir [1]. Poincaré a sûrement dû espérer pouvoir classifier de la même manière les variétés de dimension $3$. Ce problème est toutefois bien plus subtil. La notion de hiérarchie est un développement de ces idées ; elle joue encore aujourd’hui un rôle fondamental en topologie de la dimension $3$. [2]

$$ $$

Poincaré donne un critère pour que la variété soit orientable : toute identification entre deux faces $F$ et $F'$ de codimension $1$ dans $P$ doit renverser l’orientation de $F$ et $F' \subset \partial P$ induite par un choix d’orientation de $P$. [3]

Poincaré donne comme premier exemple celui d’un carré $ABCD$, comme sur la figure suivante, où l’on identifie les côtés opposés, à savoir $AB$ avec $DC$ et $AD$ avec $BC$.

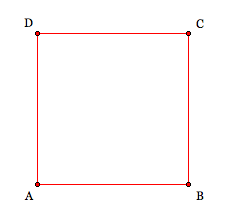
On obtient ainsi le tore. Cette identification est d’ailleurs la seule manière d’identifier les côtés opposés d’un quadrilatère tout en vérifiant le critère d’orientabilité de Poincaré. Les deux autres identifications possibles, à savoir

$$AD \equiv CB, \ AB \equiv DC$$

et

$$AD \equiv CB, \ AB \equiv CD,$$

donnent des surfaces non-orientables, respectivement la bouteille de Klein et le plan projectif réel.

La situation est plus riche en dimension $3$. Poincaré considère ainsi l’exemple du cube $P=ABCDA'B'C'D'$ auquel on consacre également tout une rubrique, avec beaucoup d’images, dans le parcours par les exemples.

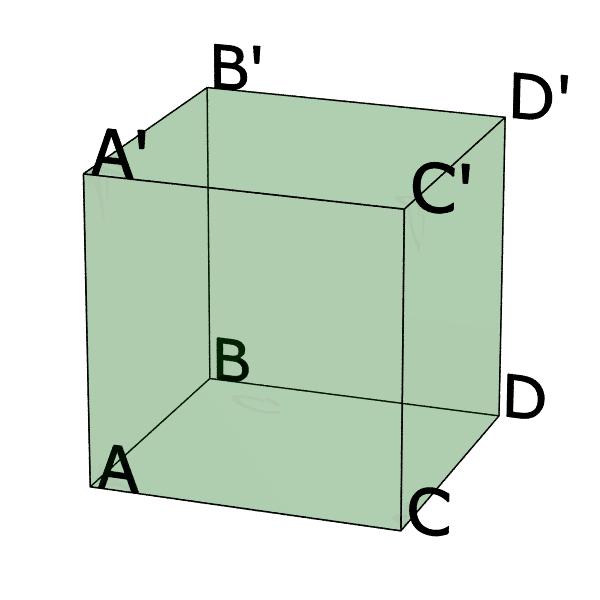
Étant donné que l’on peut maintenant faire tourner les faces, il y a beaucoup plus de manières d’identifier les faces opposées d’un cube sans violer le critère d’orientabilité. Poincaré ne considère pas toutes les possibilités mais seulement cinq :

$$ \begin{array}{|c|c|c|c|c|c|} \hline \mathrm{faces} & \mathrm{Exemple} \ 1 & \mathrm{Exemple} \ 2 & \mathrm{Exemple} \ 3 & \mathrm{Exemple} \ 4 & \mathrm{Exemple} \ 5 \\ \hline ABDC \equiv & A'B'D'C' & B'D'C'A' & B' D' C' A' & B' D' C' A' & D' C' A' B' \\ \hline ACC'A' \equiv & BDD'B' & DD'B'B & DD'B'B & BDD'B' & D'B'BD \\ \hline ABB'A' \equiv & CDD'C' & DD'C'C & C'CDD' & CDD'C' & D'C'CD \\ \hline \end{array} $$

L’exemple 1 est celui du quotient de $\mathbb{R}^3$ par le réseau $\mathbb{Z}^3$, autrement dit celui du tore tridimensionnel. L’exemple 5 est celui de l’espace projectif réel de dimension 3. Noter d’ailleurs que, de manière plutôt surprenante [4], Poincaré ne présente pas l’exemple 5 comme suggéré ci-dessus mais en donne une description équivalente par identification des points antipodaux du bord d’un octaèdre — le polyèdre régulier dual du cube.

Commentaires sur les variétés « platoniques ».

Il n’y a que $5$ polyèdres réguliers en dimension $3$ — ou polyèdres de Platon — à savoir : le tétraèdre, le cube, l’octaèdre, l’icosaèdre et le dodécaèdre. Le fait qu’il n’y en ait pas plus peut se déduire de la formule d’Euler selon laquelle pour toute cellulation de la sphère de dimension $2$ , on a

où $s$, $a$ et $f$ sont respectivement le nombre de sommets, d’arêtes et de faces de la cellulation. Si la cellulation est régulière, alors un même nombre $r$, resp. $t$, d’arêtes sont incidents à chaque face, resp. sommet, de la cellulation. Une arête étant incidente à exactement deux faces et deux sommets, on a donc :

$$rf = 2a = ts.$$

En multipliant la formule d’Euler par $rt$, on obtient donc :

$$a(2r - rt +2t) = 2rt.$$

En particulier $2r-rt+2t$ est strictement positif et, en utilisant le fait que les entiers $r$ et $t$ sont supérieurs ou égaux à $3$, on obtient que

$$\{ r,t \} = \{ 3 \}, \ \{3,4 \} \mbox{ ou } \{ 3,5 \}.$$

Bien sûr, ce n’est pas la preuve que l’on trouve dans les Éléments d’Euclide. Le point de départ est plutôt le fait que la somme des angles des faces en un sommet d’un polyèdre convexe est strictement inférieur à quatre angles droits... On recommande au lecteur qui n’a jamais vu cette preuve de la reconstruire à partir de ce point de départ.

Poincaré ne considère que certaines identifications des faces du cube et de l’octaèdre régulier. Un exemple particulièrement riche est pourtant obtenu en considérant le dodécaèdre régulier, dont on identifie chaque paire de faces opposées par une translation suivie d’une rotation d’un dixième de tour --- autrement dit, d’angle $\pi/5$. Dans le cinquième complément Poincaré décrira par une autre méthode la variété que l’on obtient ainsi et que l’on appelle de nos jours variété dodécaédrique de Poincaré. Nous verrons que Poincaré montre — toujours dans le cinquième complément — que la variété dodécaédrique de Poincaré est une sphère d’homologie mais n’est pas difféomorphe à la sphère $\mathbb{S}^{3}$.

$$ $$

Les quotients du cube considérés par Poincaré ne sont pas nécessairement des variétés. Poincaré se propose donc ensuite de donner un critère simple pour que l’espace obtenu en identifiant deux à deux les faces d’un polyèdre $P$ de dimension $3$ soit effectivement une variété.

Dans un complexe cellulaire, l’étoile d’une cellule (ouverte) $\sigma$ est constituée de toutes les cellules dont $\sigma$ est une face. Les intersections de ces cellules avec le bord d’une petite boule centrée en un point de $\sigma$ et transverse à cette cellule, constitue le link de $\sigma$. Pour cette dernière construction, on considère que, localement au voisinage de ce point, le complexe est plongé de manière différentiable dans un espace $\mathbb{R}^n$, et que la boule est prise dans un sous-espace affine transverse à l’espace tangent à la cellule $\sigma$ au point considéré.

On peut montrer que dans une cellulation lisse d’une variété, le link d’un sommet de cette cellulation est toujours une sphère. Il n’est par ailleurs pas difficile de vérifier que si $\sigma$ est une cellule de codimension $\leq 2$ dans un quotient $P /\iota$, alors son link est une sphère. Mais en général il peut y avoir des singularités en codimension $\geq 3$.

Poincaré vérifie ainsi que des cinq exemples du tableau ci-dessus, seul l’exemple 2 n’est pas une variété. Ce dernier présente deux singularités dont les links sont des tores (de dimension $2$). Les autres exemples sont donc tous des variétés orientables de dimension $3$ dont nous verrons plus loin qu’elles sont toutes distinctes (à difféomorphisme près).

$$ $$

Démonstration de la proposition. L’absence de singularités de codimension $\leq 2$ implique que les links des singularités possibles du quotient, c’est-à-dire les links des sommets de $P/\iota$, sont des surfaces. Mais une surface est difféomorphe à la sphère $\mathbb{S}^{2}$ si et seulement si sa caractéristique d’Euler est égale à $2$.

C.Q.F.D.

$$ $$

Étant donné un sommet $\alpha$ de $P/\iota$, on note respectivement $s_\alpha$, $a_\alpha$ et $f_\alpha$ le nombre de sommets, arêtes et faces dans le link de $\alpha$. Le nombre $f_\alpha$ est aussi le nombre de sommets de $P$ dans la classe du sommet $\alpha$ de $P/\iota$. Le nombre $a_\alpha$ est aussi la moitié de la somme du nombre de faces de codimension $1$ de $P$ incidentes à un sommet de la classe de $\alpha$. Et $s_\alpha$ est égale au nombre de classes d’arêtes incidentes à un sommet de la classe de $\alpha$ (en faisant bien attention de compter deux fois une classe d’arêtes dont les deux extrémités sont dans la classe de $\alpha$).

Un critère équivalent.

Le critère de Poincaré consiste à vérifier que pour tout $\alpha$, on a $s_\alpha - a_\alpha + f_\alpha =2$. Puisque l’on a toujours $s_\alpha - a_\alpha + f_\alpha \leq 2$, ce critère peut être reformulé plus simplement en demandant que

$$\tag{1} \sum_\alpha s_\alpha - a_\alpha + f_\alpha =2 c_0,$$

où $c_0$ désigne le nombre de sommets dans le quotient $P/\iota$. Maintenant, en notant plus généralement $c_i$ le nombre de cellules de dimension $i$ dans le quotient $P/\iota$, on a

$$\sum_\alpha s_\alpha = 2 c_1 \mbox{ et } c_3 = 1$$

alors que $c_2$ est égal à la moitié du nombre $F$ de faces de $P$. Ensuite $\sum_\alpha f_\alpha$ est égal au nombre $S$ de sommets de $P$ et $\sum_\alpha a_\alpha$ est égal au nombre $A$ d’arêtes de $P$. On conclut donc que l’équation (1) est équivalente à

$$2c_0 - 2c_1 = S - A (= 2-F \mbox{ d'après la formule d'Euler})$$

soit

$$2(c_0 - c_1 + c_2 -c_3) = 0.$$

On obtient ainsi un critère équivalent — un peu plus simple à énoncer — que l’on trouve par exemple dans le livre de Seifert et Threlfall [5], voir aussi ici.

$$ $$

Un calcul simple permet de vérifier que $s_\alpha - a_\alpha + f_\alpha$ est bien égal à $2$ dans chacun des exemples de Poincaré, à l’exception de l’exemple 2. Dans ce dernier on dénombre deux classes de six arêtes et deux classes de quatre sommets, comme représenté dans la figure ci-contre.

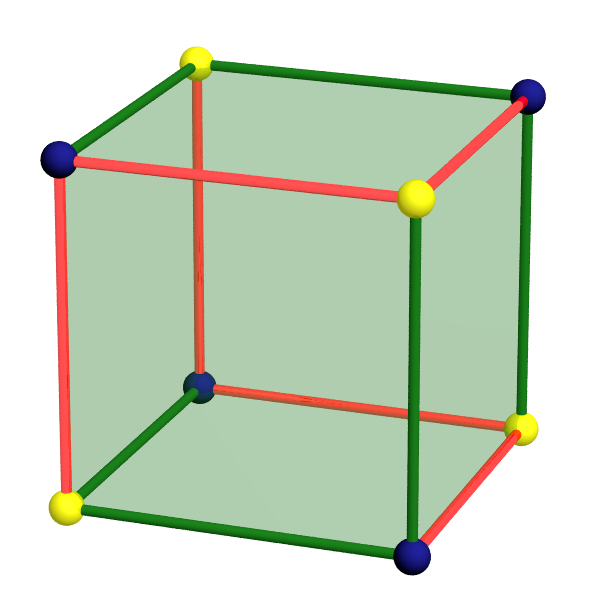
La caractéristique d’Euler du quotient est donc $2-2 +3 -1 = 2 \neq 0$. Il ne s’agit donc pas d’une variété. Afin de mieux comprendre cet espace, décrivons le link $L_p$ de l’un quelconque de ses points $p$. Le nombre $f_p$ de faces du link $L_p$ de $p$ dans $V$ est $4$, nombre de sommets du cube ayant $p$ pour image dans $V$. Chacun de ces sommets est de valence $3$ dans le cube, donc le nombre $a_p$ d’arêtes de $L_p$ est $\tfrac12 \sum_{j=1}^4 3=6$. Enfin, le nombre $s_p$ de sommets de $L_p$ est le nombre de classes d’arêtes contenant l’un des antécédents de $p$ (comptées une seule fois car chacune ne contient qu’un de ces antécédents), soit $2$. Ainsi, $\chi(L_p)=4-6+2=0$, donc $L_p$ est un tore, puisque c’est une surface fermée orientable.

Exemple 2 et suspensions.

Nous venons de voir que l’exemple 2 n’est pas une variété, ceci est illustré ici. Les deux sommets ont pour voisinage le cône sur un tore. Ces singularités interviennent naturellement lorsque l’on prend la suspension d’une variété.

Étant donné une variété lisse $X$, on appelle suspension de $X$ l’espace, que l’on note $S(X)$ obtenu en recollant deux copies du cône $C(X)$ le long de leurs bases $X$.

La suspension du tore $S(\mathbb{T}^2 )$ est une variété de dimension $3$ avec deux points singuliers dont les deux sommets ont pour voisinage le cône sur un tore. Toutefois, le calcul de son groupe fondamental montre que l’espace topologique obtenu par le recollement du cube de l’exemple 2 n’est pas homéomorphe à la suspension du tore de dimension $2$.

Intuitivement on s’attend à ce que la suspension $S(X)$ sur une variété soit encore une variété topologique de dimension $n+1$ si et seulement si $X$ est difféomorphe à la sphère $\mathbb{S}^{n}$ (auquel cas $S(X)$ est bien sûr homéomorphe à la sphère de dimension $n+1$). C’est effectivement vrai. Mais ce résultat est subtil : Cannon et Edwards [6] montrent en effet que la double suspension $S(S(X))$ d’une sphère d’homologie $X$ de dimension $n$ est homéomorphe à la sphère de dimension $n+2$. Noter que si l’on prend par exemple pour espace $X$ la sphère d’homologie de Poincaré, on obtient une cellulation topologique de la sphère de dimension $5$ dont un link est la suspension $S(X)$ qui n’est même pas une variété topologique !

Remarquons enfin qu’une variété topologique compacte (avec ou sans bord) n’est pas nécessairement triangulable [7].

On peut démontrer que la sphère d’homologie de Poincaré peut être plongée topologiquement dans $\mathbb{R}^4$ [8], mais pas différentiablement [9].