Le but de ce cinquième complément, comme annoncé dans le §1, est de construire une sphère d’homologie, c’est-à-dire une variété fermée connexe de dimension 3 dont les groupes d’homologie sont triviaux, mais qui n’est pas homéomorphe à la sphère $\mathbb{S}^3$ (puisque son groupe fondamental n’est pas trivial). Cette variété sera obtenue par recollement de deux corps en anses de genre 2 le long de leurs bords. Nos commentaires sur ce premier paragraphe se trouvent ici :
Mais les cinq premiers paragraphes sont remplis de résultats qui ne sont pas strictement nécessaires à cette construction, non plus qu’à la vérification que la variété obtenue possède bien les propriétés désirées. On peut penser que Poincaré cherche à mettre en place une théorie générale des variétés de dimension 3, en livrant en particulier sa vision de la théorie des diagrammes de Heegaard [1] [2]. Dans les premiers paragraphes de son mémoire, Poincaré semble en effet nous expliquer avec quels outils il a pu répondre à des questions comme :
- une famille de courbes fermées tracées sur le bord d’un corps en anses forment-elles une famille maximale de courbes de compression ?
- quel est le groupe fondamental d’une variété obtenue par recollement de deux corps en anses ?
- quel est le premier groupe d’homologie d’une telle variété ?
Détaillons un peu :
Avec les scindements de Heegaard en tête, Poincaré commence par développer tout un embryon de « théorie de Morse » dans le §2. Il pense en effet sa variété et ses corps en anses comme des « empilements de niveaux de fonctions ». Il se servira cependant à peine de cet embryon de théorie, si ce n’est pour retrouver la classification des surfaces. Nos commentaires sur le deuxième paragraphe se trouvent ici :
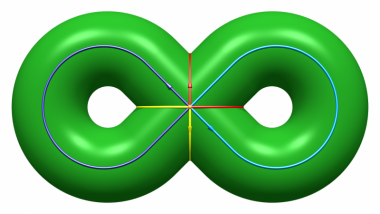
Considérons une 3-variété fermée $V$ obtenue par recollement de deux corps en anses de genre deux le long de leurs bords. La figure ci-dessous représente l’un de ces deux corps en anses, noté $V'$. Comme Poincaré l’explique dans le §6, s’appuyant sur le §5, pour déterminer le groupe fondamental et le premier groupe d’homologie de $V$, il lui suffit de connaître les images $C_1'$ et $C_3'$ des courbes $C_1$ (rouge) et $C_3$ (jaune) sur la figure ci-dessous par l’homéomorphisme de recollement [3].
En effet, on vérifiera que le groupe d’homologie $H_1(V)$ (resp. le groupe fondamental $\pi_1(V)$) est le quotient de $H_1(V')$ (resp. $\pi_1(V')$), par le sous-groupe engendré par les classes des courbes $C'_1$ et $C'_3$. Il est engendré par les classes des $C_2$ (bleu clair) et $C_4$ (bleu foncé).
L’exercice auquel se soumet Poincaré est donc de trouver deux lacets $C'_1$ et $C'_3$ sur le bord du second corps en anse :
- qui soient images de $C_1$ et $C_3$ par un homéomorphisme,
- qui engendrent le premier groupe d’homologie du corps en anses,
- qui n’engendrent pas son groupe fondamental.
Poincaré se ramène à un problème combinatoire en cherchant les solutions (à homotopie près) sous forme de combinaisons des « lacets fondamentaux » $C_1,C_2,C_3,C_4$, ce qui nécessite de traduire les propriétés ci-dessus en ces termes.
Le §3 et le §4 traitent du premier point. Deux mots arbitraires en les lacets fondamentaux ne correspondent pas forcément à deux lacets images de $C_1$ et $C_3$ par un homéomorphisme (deux tels lacets images devant notamment être simples et disjoints). Il s’agit de déterminer quels sont les paires de mots « admissibles ». Nos commmentaires sur ses deux paragraphes sont accessibles dans les deux rubriques suivantes :
Le deuxième point est étudié dans le §6, à la suite de quoi Poincaré fournit finalement « sa » solution, dont il vérifie, toujours dans le §6, qu’elle satisfait bien aussi le troisième point. [4]
Mais, comme nous l’avons dit, Poincaré ne se contente pas de résoudre ces questions précises. Il développe à chaque étape des notions et arguments beaucoup plus généraux, dont nous rendrons compte dans les commentaires détaillés de chaque partie. Au final ce cinquième complément est tout simplement, avec le mémoire de Heegaard, l’acte de naissance de la topologie de dimension 3. Le lecteur pourra trouver nos commentaires sur les paragraphes 5 et 6 dans les rubriques :
[1] sans d’ailleurs faire la moindre allusion à ce dernier, dont il a pourtant dû lire en partie les travaux suite à ses objections concernant le premier complément...
[2] On rappelle qu’une scindement de Heegaard d’une 3-variété fermée $V$ est une décomposition de $V$ comme union de deux corps en anses d’intérieurs disjoints. Un diagramme de Heegaard est un moyen combinatoire de coder la manière dont on recolle deux corps en anses le long de leur bords. Voir le ici pour plus de détails.
[3] Ou plutôt par l’application induite en homologie et en homotopie.
[4] L’impression finale est que, ayant suffisamment réduit l’ensemble des combinaisons possibles grâce aux points 1 et 2, Poincaré s’est mis à tester des combinaisons jusqu’à en trouver une qui marche.