§2 du cinquième complément

Je considère une variété $V$ à $m$ dimensions située dans l’espace à $k$ dimensions [1]. Soit ensuite

$$ \varphi (x_1 , x_2 , \ldots , x_k ) =t $$

l’équation d’une surface à $k-1$ dimensions située dans ce même espace et que j’appellerai la surface $\varphi (t)$ ; dans cette équation $x_1 , x_2 , \ldots , x_k$ sont les coordonnées d’un point dans l’espace à $k$ dimensions et $t$ un paramètre arbitraire tel que la surface $\varphi (t)$ se déforme d’une manière continue quand $t$ varie d’une manière continue [2]. Je supposerai que la fonction $\varphi$ est uniforme de telle façon que par un point quelconque passe une surface $\varphi (t)$ et une seule.

La surface $\varphi (t)$ coupera $V$ suivant un certain nombre de variétés [3] à $m-1$ dimensions

$$ w_1 (t) , w_2 (t) , \ldots , w_p (t) $$

dont l’ensemble formera le système $W (t)$.

Quand $t$ variera d’une manière continue de $-\infty$ à $+\infty$, le système $W(t)$ variera d’une manière continue et engendrera la variété $V$. Si la variété $V$ est fermée, les variétés $w(t)$ le seront également.

Cela posé, je vais définir ce que j’appellerai le squelette de la variété $V$. À chacune des variétés partielles $w_1 (t) , w_2 (t) , \ldots , w_p (t)$ je ferai correspondre un point dans l’espace ordinaire. L’une des coordonnées de ce point, $x$ par exemple, sera égale au paramètre $t$, les deux autres seront choisies arbitrairement, en s’assujettissant seulement aux conditions suivantes :

1. Si deux variétés $w_i (t)$, $w_i (t+ \epsilon )$ sont très peu différentes l’une de l’autre, les deux points correspondants devront être très voisins l’un de l’autre.

2. Il peut arriver que pour certaines valeurs de $t$, pour $t=t_0$ par exemple, une des variétés $w(t)$ se décompose en deux autres ; dans ce cas, par exemple, la variété $w_1 (t_0 - \epsilon )$ différera très peu de l’ensemble des deux variétés $w_1 (t_0 + \epsilon ) + w_2 (t_0 + \epsilon )$. Dans ce cas, on doit s’arranger de façon que les deux points qui représentent les deux variétés $w_1 (t_0 + \epsilon )$ et $w_2 (t_0 + \epsilon )$ qui résultent du dédoublement de $w_1 (t_0 - \epsilon )$, que ces deux points, dis-je diffèrent très peu l’un de l’autre et très peu du point représentatif de $w_1 (t_0 - \epsilon )$.

Dans ces conditions, quand $t$ variera d’une manière continue, les points représentatifs des $p$ variétés

$$ w_1 (t) , w_2 (t) , \ldots , w_p (t) $$

engendreront $p$ lignes continues

$$ L_1 , L_2 , \ldots , L_p, $$

du moins tant que le nombre $p$ ne varie pas. Mais ce nombre peut varier pour $t = t_0$, si l’une des variétés se décompose en deux, ou si, au contraire, deux variétés se réunissent en une seule. Dans le premier cas, l’une des lignes $L$ se bifurque, dans le second deux des lignes $L$ se réunissent en une seule.

On obtient ainsi une sorte de réseau de lignes, et c’est ce réseau que j’appelle le squelette de $V$. J’ai tracé ce réseau dans l’espace à trois dimensions et non dans le plan, parce qu’on peut ainsi toujours éviter que deux lignes se coupent en d’autres points que les points de bifurcation.

Si nous suivons l’une de ces lignes, $L_1$ par exemple, décrite par le point représentatif de $w_1 (t)$, nous voyons que cette variété $w_1 (t)$ reste constamment homéomorphe à elle-même [et cela de telle façon que sur les deux variétés très voisines $w_1 (t)$ et $w_1 (t+\epsilon )$, deux points correspondants diffèrent très peu l’un de l’autre] tant que l’on ne passe pas par une valeur de $t$ telle que $w_1 (t)$ ait un point singulier.

Nous devons donc marquer sur les lignes de notre réseau les points qui correspondent aux variétés $w(t)$ qui ont des points singuliers. Ce seront des points de division qui partageront nos lignes en tronçons, mais tant qu’on suivra l’un de ces tronçons, la variété $w(t)$ correspondante restera homéomorphe à elle-même.

Remarquons que si l’on considère une des valeurs $t_0$ qui correspondent aux points de bifurcation, et pour lesquelles une des variétés $w_i$ se dédouble, la variété $w_i (t_0)$ admet également un point singulier. Cela va donc nous obliger, à étudier ces points singuliers.

Mais avant de procéder à cette étude, je dois faire encore quelques remarques. Si je veux que la variété $V$ soit fermée, il faut d’abord que les variété [4] $w(t)$ soient fermées elles-mêmes. La seconde condition c’est que, si l’une de mes lignes $L$ aboutit à un cul-de-sac, de telle façon qu’elle s’arrête pour $t=t_1$ par exemple, la variété correspondante tende à se réduire à un point quand $t$ tend vers $t_1$, c’est-à-dire quand on se rapproche du cul-de-sac.

En second lieu, j’ai dit que je choisissais la fonction $\varphi$ uniforme, de telle façon que par un point de l’espace passe une surface $\varphi = t$ et une seule. Dans ces conditions, le système $W(t)$ n’est pas quelconque. Cette restriction ne m’a pas empêché de montrer que toute variété $V$ est susceptible de ce mode de génération, mais on peut s’en affranchir et considérer un système quelconque $W(t)$ de variétés fermées

$$ w_1 (t) , w_2 (t) , \ldots , w_p (t) $$

pourvu que ces variétés varient d’une manière continue avec $t$, en supposant bien entendu que pour certaines valeurs de $t$, une de ces variétés puisse se réduire à un point, ou se décomposer en deux autres.

Dans ces conditions, le système $W(t)$ engendrera encore une variété $V$ et l’on pourra en définir le squelette d’après les mêmes principes auxquels il n’y aura rien à changer.

Il y a cependant un cas où l’on pourra avec avantage y faire un léger changement. J’imagine que pour deux valeurs de $t$, par exemple pour $t=0$ et pour $t=2\pi$, le système $W(t)$ soit le même, ou mieux, j’imagine que les deux systèmes $W(t)$ et $W(t + 2\pi )$ soient identiques. Il suffit alors de faire varier $t$ de $0$ à $2\pi$, et il convient, par conséquent, de choisir le point représentatif de la variété $w(t)$, non plus de telle façon que l’on ait $x=t$, mais de telle façon que $\mathrm{arc \ tg} \frac{y}{x} = t$, c’est-à-dire que les points représentatifs de $w(t)$ et $w(t+2\pi )$ puissent être identiques.

Si nous supposons, par exemple, que $W(t)$ se réduise à une seule variété $w(t)$, le squelette de $V$ se réduira dans ces conditions à une courbe fermée.

Pour prendre un exemple tout à fait simple, considérons un tore qui sera notre variété $V$ et regardons-le comme engendré par son cercle méridien qui sera notre variété $w(t)$, identique à $w(t+2\pi )$. Avec nos nouvelles conventions, le squelette de ce tore se réduit à une courbe fermée.

Abordons maintenant l’étude des points singuliers des variétés $w(t)$. La portion d’une de ces variétés voisine du point singulier pourra être représentée par les équations suivantes :

$$ \begin{split} & x_i = \psi_i (y_1 , y_2 , \ldots , y_q ) \quad (i=1 , 2 , \ldots , k), \\ & \varphi_h (y_1 , y_2 , \ldots , y_q ) = 0 \quad (h=1 , 2 , \ldots , q-m ) \end{split} $$

auxquelles il conviendrait d’adjoindre certaines inégalités dont nous n’avons pas à nous occuper.

Dans la région envisagée, les fonctions $\varphi$ et $\psi$ sont holomorphes. Nous pouvons toujours supposer que le point singulier correspond à

$$ y_1 = y_2 = \ldots = y_q = 0 $$

et que pour cette valeur les dérivées partielles du premier ordre des fonctions $\varphi$ ne sont pas toutes nulles, sauf pour l’une d’entre elles $\varphi_1$.

Alors, des équations

$$ \varphi_2 = \varphi_3 = \ldots = \varphi_{q-m} = 0 $$

nous pourrons tirer tous les $y$ en fonction de $m+1$ d’entre eux, lesquelles fonctions resteront holomorphes dans le voisinage du point singulier. Je remplacerai donc les $y$ par les expressions ainsi trouvées, de sorte que tout se trouvera exprimé en fonction de $m+1$ des quantités $y$, par exemple de $y_1 , y_2 , \ldots , y_{m+1}$ et que nos équations prendront la forme

$$ \begin{split} & x_i = \psi_i (y_1 , \ldots , y_{m+1}),\\ & \varphi_1 (y_1 , \ldots , y_{m+1}) = 0. \end{split} $$

La fonction $\varphi_1$ est développable suivant les puissances des $y$ et ce développement commence par des termes du second degré dont l’ensemble constitue une forme quadratique $f (y_1 , \ldots , y_{m+1})$.

Il est inutile d’envisager les points singuliers des autres types, car s’il y en avait, il suffirait pour les faire disparaître de changer très peu la fonction $\varphi (x_1 , \ldots , x_k )$ qui définit les surfaces $\varphi (t)$, du moins si l’on suppose que la variété $V$ est elle-même dépourvue de point singulier. Nous sommes ainsi amené à étudier le cône du second degré

$$ f (y_1 , \ldots , y_{m+1})=0 $$

dans l’espace à $m+1$ dimensions des $y$, et son intersection avec l’hypersphère

$$ y_1^2 + y_2^2 + \ldots + y_{m+1}^2 = 1. $$

Soit $C$ cette intersection. Tout dépendra du nombre des dimensions et du nombre des carrés positifs et négatifs dans la décomposition de la forme $f$ en une somme de carrés.

Nous pouvons toujours par un changement de coordonnées ramener $f$ à la forme

$$ f= \sum A_i y_i^2 - \sum B_k y_k^2 , $$

les coefficients $A$ et $B$ étant positifs, de façon qu’il y ait $q$ carrés positifs et $m+1-q$ carrés négatifs et que l’indice $i$ varie de $1$ à $q$ et l’indice $k$ de $q+1$ à $m+1$.

Je puis écrire alors

$$ \sum A_i y_i^2 = \sum B_k y_k^2 = \lambda^2 ; $$

d’où

$$ y_i = \eta_i \lambda , \quad y_k = \eta_k \lambda, $$

les $\eta$ étant des solutions quelconques des équations

$$ \tag{1} \sum A_i \eta_i^2 = 1, \quad \sum B_k \eta_k^2 = 1. $$

On en déduit

$$ \lambda^2 ( \sum \eta_i^2 + \sum \eta_k^2 ) = 1. $$

En tenant compte des équations (1), on verra que les limites supérieure et inférieure de $\sum \eta_i^2$ sont les inverses du plus petit et du plus grand des coefficients $A$. On trouvera, de même, une limite supérieure et inférieure de $\sum \eta_k^2$. On en conclura que $\lambda$ est une fonction continue des $\eta$ [supposés liés par les équations (1)] et que cette fonction ne peut ni s’annuler ni devenir infinie. Nous pouvons donc supposer que $\lambda$ reste toujours positif ; et alors $\lambda$ sera une fonction continue et parfaitement déterminée des $\eta$ ; il en sera donc de même des $y$.

Plusieurs cas peuvent se présenter :

1. Si $q$ est nul ou égal à $m+1$ de façon que tous les carrés soient de même signe, il est clair que le cône se réduit à un point et que $C$ n’existe pas.

2. Si $q$ n’est pas égal à $1$, on pourra passer d’une façon continue d’une solution quelconque de l’équation $\sum A_i \eta_i^2 = 1$ à une autre solution quelconque ; si, au contraire, $q=1$, cette équation ne comportera que deux solutions : $\eta_i = \pm \frac{1}{\sqrt{A_i}}$ et l’on ne pourra passer de l’une à l’autre d’une manière continue.

De même si $q$ n’est pas égal à $m$, on pourra passer d’une façon continue d’une solution quelconque de l’équation $\sum B_k \eta_k^2 = 1$ à une autre solution quelconque ; si, au contraire, $q=m$, l’équation n’aura que deux solutions et le passage sera impossible.

Outre le cas examiné plus haut, il y en a donc trois.

Si $1 < q < m$, $C$ est d’un seul tenant.

Si $1=q < m$, ou si $1 < q=m$, $C$ se compose de deux morceaux.

Si $1=q=m$, $C$ se compose de quatre morceaux, ou mieux se réduit à quatre points discrets.

Dans ce dernier cas, on a $m=1$, et la variété $V$ n’a que deux dimensions ; cela nous avertit que nous allons rencontrer une différence entre les variétés de deux ou de plus de deux dimensions.

Supposons d’abord que $V$ ait deux dimensions ($m=1$) ; nous pouvons avoir alors :

1. $q=0$ ou $q = 2$. Dans ce cas $C$ n’existe pas ; quand $t$ passe par la valeur qui correspond à un pareil point singulier, nous voyons une nouvelle variété $w(t)$ apparaître (ou disparaître) : elle se réduit d’abord à un point, puis à une petite courbe fermée. Ce point singulier correspond donc à un cul-de-sac du squelette.

2. $q=1$. Dans ce cas, $C$ se réduit à quatre points que je puis numéroter $1,2,3,4$. La variété $w(t)$ se réduit à une courbe qui admet, comme point singulier, un point double ordinaire où se croisent deux branches de courbe qui sont les branches $1.3$ et $2.4$. Je suppose que le point singulier se présente pour $t=0$ ; j’appellerai $1', 2', 3', 4'$ les points de la variété $w(t)$ qui, pour des valeurs de $t$ très petites, sont respectivement très voisins des points $1, 2, 3, 4$ de la variété $w(0)$.

Je commence par observer que la branche de courbe qui, partie du point double va au point $1$, doit revenir au point double, puisque toutes nos courbes sont fermées ; il peut y revenir par un des trois autres points $2, 3, 4$. Il en résulte que nos points $1, 2, 3, 4$ sont associés à deux, par exemple $1$ avec $2$, et $3$ avec $4$, de telle façon que l’on puisse aller de $1$ à $2$ et de $3$ à $4$ en suivant la courbe $w(0)$ et sans passer dans le voisinage du point double. De même, on pourra aller de $1'$ à $2'$ et de $3'$ à $4'$ en suivant la courbe $w(t)$ et sans passer dans le voisinage du point double, et cela pour toutes les petites valeurs de $t$, qu’elles soient positives ou négatives.

Maintenant, si nous considérons le voisinage du point double, nous voyons que pour $t<0$, par exemple, on peut passer de $1'$ à $2'$ et de $3'$ à $4'$ en suivant $w(t)$ et en passant près du point double, tandis qu’on ne peut pas passer de la sorte de $1'$ à $4'$ et de $2'$ à $3'$. Au contraire, pour $t>0$, on peut passer de $1'$ à $4'$ et de $2'$ à $3'$, mais pas de $1'$ à $2'$ et de $3'$ à $4'$.

Il en résulte que pour $t<0$, les branches envisagées de $w(t)$ forment deux courbes fermées distinctes tandis que pour $t>0$, elles n’en forment plus qu’une.

Notre point singulier correspond donc à une bifurcation du squelette.

Il en est de même si $1$ est associé avec $4$, et $2$ avec $3$.

Mais supposons maintenant que $1$ soit associé avec $3$, et $2$ avec $4$. Nous voyons alors que pour $t<0$, comme pour $t>0$, notre variété $w(t)$ se réduit à une seule courbe fermée ; seulement pour $t<0$ cette courbe passe successivement par les points $1'3'4'2'1'$, et pour $t>0$ par les points $1'3'2'4'1'$. Notre point singulier ne correspond plus alors à une bifurcation.

Mais je dis que, dans ce cas, la variété $V$ est unilatère.

Pour nous en rendre compte, prenons une surface fermée quelconque à deux dimensions (bilatère ou unilatère), décomposons-la (en la laissant d’un seul morceau) de façon à pouvoir la développer sur un plan ; nous obtiendrons ainsi un polygone, analogue aux polygones fuchsiens, dont les côtés seront conjugués deux à deux, deux côtés conjugués correspondant aux deux lèvres d’une même coupure.

Soient $AB$ et $A'B'$ deux côtés conjugués, de telle façon que le sommet $A$ soit conjugué de $A'$ et le sommet $B$ de $B'$. Si en allant de $A$ en $B$ on a l’intérieur du polygone, à sa gauche par exemple, et si en allant de $A'$ en $B'$ on a l’intérieur à sa droite, nous dirons que la conjugaison est directe.

Si, au contraire, en allant de $A$ en $B$ on a l’intérieur à sa gauche, et si en allant de $A'$ en $B'$ on a l’intérieur également à sa gauche, nous dirons que la conjugaison est inverse. (Cette convention surprendra d’abord mais elle se justifie avec un peu de réflexion). Cela posé, si toutes les paires de côtés sont conjugués directement (ainsi qu’il arrive pour les polygones fuchsiens), c’est que la surface d’où l’on était parti était bilatère. Si pour une paire de côtés, la conjugaison est inverse, c’est que cette surface était unilatère.

Supposons, par exemple que notre polygone soit un rectangle dont les sommets se succèdent dans l’ordre circulaire $ABCD$ et dont les côtés opposés soient conjugués. Si $AB$ est conjugué de $DC$, et $AD$ de $BC$, la conjugaison est directe, et le polygone peut être regardé comme provenant du développement d’un tore, surface bilatère. Si $AB$ est conjugué de $CD$, et $AD$ de $BC$, la conjugaison est inverse pour l’une des paires et directe pour l’autre, et le polygone provient du développement d’une surface unilatère analogue à celle de Môbius. Si $AB$ est conjugué de $CD$, et $AD$ de $CB$, la conjugaison est inverse pour les deux paires et le polygone provient du développement du « plan projectif » qui est une [5] surface unilatère.

Cela posé, appliquons ces règles à notre variété $V$, découpons-la et appliquons-la sur un plan de façon à obtenir notre polygone. Je ne représente sur la figure que la partie du polygone qui nous intéresse.

Nous avons en $O$ le point singulier ; les lignes $CHD$, $AEB$, $C'H'D'$, $A'E'B'$ représentent une portion du contour du polygone. Les deux lignes $E 1 O 3 E'$ et $H 2 O 4 H'$ qui se croisent en $O$ sont le développement de la courbe $w(0)$. Les lignes $B 1' 2' C$, $B' 3' 4' C'$ sont le développement de la courbe $w(t)$ pour $t<0$. Les lignes $D 2' 3' A'$ et $D' 4' 1' A$ sont le développement de la courbe $w(t)$ pour $t >0$. Par hypothèse, cette courbe $w(t)$ se ferme sur elle-même de façon que la branche $1'$ se raccorde à la branche $3'$ et la branche $2'$ à la branche $4'$.

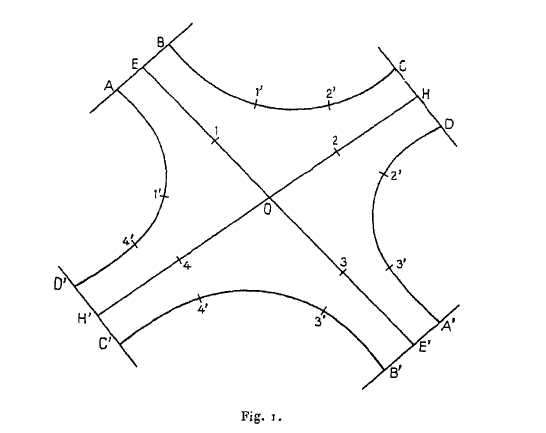
Donc $A$ doit venir se recoller à $A'$, c’est-à-dire que $A$ est conjugué de $A'$ et, de même, $B$ de $B'$, $C$ de $C'$, $D$ de $D'$. Ainsi, sur notre polygone, $AB$ est conjugué de $A'B'$, et $CD$ de $C'D'$ ; la conjugaison est inverse. Donc notre surface est unilatère.

C.Q.F.D.

Si donc $V$ a deux dimensions et est bilatère, son squelette n’aura d’autre point singulier que les culs-de-sac et les bifurcations. C’est là le secret de la simplicité relative de l’Analysis situs des surfaces ordinaires.

[<-dim3]
J’arrive aux variétés $V$ à trois dimensions ($m = 3$) auxquelles je me bornerai pour le moment. Nous avons encore à distinguer deux cas :

1. $q=0$ ou $q=3$ ; alors $C$ n’existe pas, et le point singulier correspond à un cul-de-sac du squelette.

2. $q=1$ ou $q=2$ ; alors $C$ se compose de deux morceaux ; la variété $w(0)$ présente un point conique ordinaire (si le point singulier correspond à $t=0$) ; les parties de cette variété voisines du point singulier sont assimilables à un cône du second degré ordinaire. Donnons maintenant à $t$ des valeurs très petites. Les parties de $w(t)$ voisines du point singulier seront assimilables, par exemple, à un hyperboloïde à une nappe pour $t<0$ et à un hyperboloïde à deux nappes pour $t > 0$.

Considérons l’ellipse de gorge $E$ de l’hyperboloïde à une nappe ; cette ellipse pour $t=-\epsilon$ (ou [6] $\epsilon$ est positif et très petit) est un cycle fermé très petit tracé sur $w(t)$ ; pour $t=0$, elle se réduit à un point et, pour $t=+\epsilon$, elle disparaît.

Ce que nous avons appelé $C$ (intersection du cône et de l’hypersphère) se compose ici de deux courbes fermées (on est dans le cas de $q=1$, ou $q = m$), et nous devons distinguer deux cas : ou bien on ne peut pas passer d’une de ces deux courbes fermées à l’autre en restant sur $w(t)$ et sans passer dans le voisinage du point singulier, ou bien ce passage est possible.

Dans le premier cas, l’ellipse $E$ partage la variété $w(-\epsilon )$ en deux parties, car on ne peut pas passer du voisinage de l’une des courbes $C$ au voisinage de l’autre courbe $C$ sans passer dans le voisinage du point singulier, c’est-à-dire sans couper l’ellipse de gorge $E$. On aura donc sur $w(-\epsilon )$

$$ E \sim 0. $$

Dans le second cas, au contraire, $E$ ne divisera pas $w(-\epsilon )$.

Dans le premier cas, les nappes de $w(t)$ qui vont passer dans le voiginage [7] du point singulier forment une seule surface fermée pour $t = -\epsilon$ puisqu’on peut toujours passer d’un point à l’autre d’une de ces nappes et, en particulier, du voisinage de l’une des courbes $C$ à celui de l’autre en traversant l’ellipse $E$. Au contraire, pour $t=+\epsilon$, elles formeront deux surfaces fermées, puisqu’on ne peut plus passer d’une des courbes $C$ à l’autre.

Dans ce premier cas, notre point singulier correspond donc à une bifurcation du squelette.

Dans le second cas, au contraire, ces nappes de $w(t)$ forment toujours une seule surface fermée, aussi bien pour $t=-\epsilon$ que pour $t=+\epsilon$, puisqu’on peut toujours passer d’une courbe $C$ à l’autre sans passer près du point singulier.

Dans ce second cas, notre point singulier ne correspond pas à une bifurcation.

Ce second cas se subdivise lui-même. Considérons un chemin permettant de passer d’une courbe $C$ à l’autre sans passer près du point singulier. Quand on suivra ce chemin, si l’on veut conserver la forme des équations, il faudra de temps en temps changer de variables et remplacer les variables $y$ par d’autres variables $y'$, puis les $y'$ par de nouvelles variables $y''$, etc. Nous supposerons toujours que ces changements de variables aient été faits de telle sorte que le déterminant fonctionnel des nouvelles variables par rapport aux anciennes soit positif. Soient $z_1, z_2 , \ldots , z_{m+1}$ les variables finales quand on reviendra dans le voisinage du point singulier. Nous aurons donc les $x$ en fonction des $z$ mais comme dans le voisinage du point singulier, nos équations qui donnent les $x$ en fonction des $y$ redeviennent valables, les séries redevenant convergentes, nous aurons les $z$ en fonction des $y$ ; deux cas peuvent donc se présenter selon que le déterminant fonctionnel des $z$ par rapport aux $y$ est positif ou négatif. Dans le premier cas le chemin est bilatère, dans le second cas unilatère. C’est ce que j’ai expliqué dans l’Analysis situs, en définissant les variétés unilatères.

Alors s’il existe des chemins qui permettent de passer d’une courbe $C$ à l’autre sans passer dans le voisinage du point singulier : ou bien tous ces chemins seront bilatères, ou bien les uns seront bilatères et les autres unilatères, ou bien enfin ils seront tous unilatères.

Pour le moment nous nous bornerons au cas où toutes les surfaces $w(t)$ seront bilatères. Tous nos chemins, s’ils existent, seront donc bilatères.

Nous savons que pour une surface bilatère, le nombre de Betti est toujours impair. Si donc une surface bilatère est $2p + 1$ fois connexe, elle admettra $2p$ cycles distincts, c’est-à-dire dont aucune combinaison linéaire n’est holomogue [8] à zéro. Envisageons donc les $2p$ cycles de la surface $w(-\epsilon )$, nous ferons d’abord entre eux une distinction, ceux qui rencontrent l’ellipse de gorge $E$ et ceux qui ne la rencontrent pas. Si un cycle $K$ rencontre $E$, nous devrons distinguer les points de rencontre en deux catégories suivant le signe d’un certain déterminant, ainsi que je l’ai expliqué dans l’Analysis situs, page 219. Nous définirons ainsi le nombre $N(K, E)$ (cf. Analysis situs p. 220), qui sera la différence des nombres des points d’intersection des deux catégories. Si le nombre $N$ relatif au cycle $K$ est nul, le cycle $K$ sera homologue à un cycle qui ne rencontre $E$ pas. Si, au contraire, ce nombre $N$ n’est pas nul, tous les cycles homologues à $K$ rencontreront $E$.

Qu’arrive-t-il alors, quand $t$ variant d’une façon continue passe de la valeur $-\epsilon$ à la valeur $\epsilon$ ? On pourra trouver sur $w(+\epsilon)$ une ligne $K'$ infiniment peu différente du cycle $K$ tracé sur $w(-\epsilon)$ ; seulement si $K$ ne rencontre pas $E$, la ligne $K'$ est fermée et constitue un nouveau cycle sur $w(\epsilon)$ ; si, au contraire, $K$ rencontre $E$, la ligne $K'$ ne peut être fermée. Donc, pour qu’il y ait sur $w(\epsilon)$ des cycles infiniment peu différents d’un cycle homologue à $K$, il faut et il suffit que le nombre $N(K, E)$ soit nul.

En d’autres termes tous les cycles pour lesquels ce nombre n’est pas nul, disparaîtront quand $t$ passera de $-\epsilon$ à $+\epsilon$, tous les autres subsisteront.

Soit $K$ un cycle de $w(-\epsilon)$ qui subsiste et $K'$ le cycle correspondant de $w(\epsilon )$.

Dans quels cas aura-t-on $K' \sim 0$ ?

Si l’on a $K' \sim 0$, il existera sur $w(\epsilon )$ une aire $A'$ limitée par $K'$ ; on pourra trouver sur $w(-\epsilon)$ une aire $A$ infiniment peu différente de $A'$, et cette aire sera limitée par $K$ seulement on par $K$ et par l’ellipse de gorge $E$, de sorte qu’on aura

$$ K \sim 0 \quad \text{ou} \quad K \sim E. $$

J’ajoute que si nous traçons sur $w(\epsilon)$ un cycle quelconque $K'$ nous pourrons toujours trouver sur $w(-\epsilon )$ un cycle $K$ qui en diffère très peu, et que l’on ne peut avoir $K \sim 0$ sans avoir $K' \sim 0$ ; car s’il existe sur $w( -\epsilon)$ une aire $A$ limitée par $K$, il existera sur $w(\epsilon )$ une aire $A'$ limitée par $K'$ et très peu différente de $A$.

Donc, quand $t$ passe de $-\epsilon$ à $+\epsilon$, certains cycles peuvent disparaître, mais des cycles nouveaux ne peuvent pas apparaître ; certains cycles peuvent devenir homologues à zéro, mais aucun cycle ne peut cesser de l’être de sorte que le nombre de Betti $2p + 1$ peut décroître, mais ne peut pas croître.

Il résulte de là que deux cas seulement peuvent se présenter :

1. Ou bien $E \sim 0$ sur $w(-\epsilon)$ ; dans ce cas, nous avons vu que quand $t$ passe de $-\epsilon$ à $+\epsilon$, la variété $w(t)$ se décompose en deux autres.

Les cycles de $w(-\epsilon)$ ne peuvent pas disparaître ; en effet comme on a $E \sim 0$, on aura $N(K, E) = 0$ pour tous les cycles $K$. De plus, aucun de ces cycles $K$ ne peut devenir homologue à zéro. Nous avons vu, en effet, quelles étaient les nouvelles homologies qui pouvaient s’introduire entre les cycles $K$, par suite du passage de $t$ de $-\epsilon$ à $+\epsilon$ ; on peut toutes les déduire de l’homologie nouvelle $E \sim 0$ ; et, en effet, nous avons dit que pour que l’on ait $K' \sim 0$ sans avoir $K \sim 0$, il faut que l’on ait $K \sim E$. Or, dans le cas qui nous occupe, nous avons $E \sim 0$, aussi bien sur $w(-\epsilon)$ que sur $w(\epsilon)$. Il ne s’introduit donc pas d’homologie nouvelle.

Le nombre total des cycles distincts demeure donc le même ; si $w (-\epsilon)$ est $2p+1$ fois connexe, $w(\epsilon )$ se décomposera en deux surfaces qui seront respectivement $2p'+1$ fois et $2p''+1$ fois connexes, où $p' + p'' = p$.

2. Dans le second cas, on n’a pas $E \sim 0$ sur $w (-\epsilon)$, nous avons vu que, dans ce cas, $w(t)$ ne se décompose pas ; nous supposons que $w( -\epsilon )$ est $2p+1$ fois connexe et possède $2p$ cycles distincts. Au moment où $t$ devient positif, certains cycles $K$ disparaissent ; ce sont ceux qui sont tels que $N(K, E)$ ne soit pas nul. Mais si l’on a deux cycles $K_1$ et $K_2$ tels que

$$ N(K_1 , E) = m_1 , \quad N(K_2 , E) = m_2, $$

alors on aura

$$ N(m_2 K_1 - m_1K_2, E) = 0, $$

de sorte que le cycle $m_2 K_1 - m_1K_2$ ne disparaît pas. Il résulte de là que tous les cycles qui disparaissent sont toujours une combinaison linéaire de l’un d’entre eux et des cycles qui ne disparaissent pas. Le nombre des cycles distincts diminue donc de ce fait d’une unité, et d’une seule.

D’autre part, entre les cycles subsistants, s’introduit une homologie nouvelle, et une seule,

$$ E \sim 0, $$

de sorte que le nombre des cycles diminue encore d’une unité.

En résumé, le nombre total des cycles distincts diminue en tout de deux unités, de sorte que $w(\epsilon)$ est $2p -1$ fois connexe.