§4 du cinquième complément

Nous avons vu au paragraphe précédent qu’il est relativement aisé de reconnaître si un cycle donné est homologue à un cycle non bouclé, ou si deux cycles donnés sont respectivement homologues à deux cycles qui ne se coupent pas. Nous allons dans le présent paragraphe examiner une question analogue :

Comment reconnaître si un cycle donné est équivalent à un cycle non bouclé, ou si deux cycles donnés sont équivalents à deux cycles qui ne se coupent pas ?

Mais avant d’aborder cette question, revenons sur la définition de l’équivalence.

Jusqu’ici nous avons toujours entendu cette équivalence de la façon suivante :

Quand nous écrivons

$$C\equiv C',$$

nous entendons que le point initial et final du cycle fermé $C$ est le même que le point initial et final de $C'$, et qu’il existe entre $C$ et $C'$ une aire simplement connexe dont la frontière complète est formée par $C$ et $C'$. Ou, en d’autres termes, que l’on peut passer de $C$ à $C'$ en faisant varier $C$ d’une manière continue et de façon que le cycle reste constamment formé d’une seule courbe fermée et que le point initial et final demeure invariable. C’est ce qu’on peut appeler l’équivalence propre.

Nous pouvons avoir avantage à écrire

$$C\equiv C' \quad \textrm{(impr.)}$$

quand on peut passer de $C$ à $C'$ en faisant varier $C$ d’une manière continue de façon que le cycle reste constamment formé d’une seule courbe fermée, mais en faisant varier le point initial et final. C’est ce qu’on peut appeler l’équivalence impropre. En d’autres termes, on aura l’équivalence impropre

$$C\equiv C' \quad \textrm{(impr.)}$$

quand on aura l’équivalence propre

$$C\equiv -\alpha + C' + \alpha,$$

$\alpha$ étant un arc quelconque, allant du point initial et final de $C'$ au point initial et final de $C$.

Nous aurons donc quatre sortes de relations : les équivalences propres, où l’on n’a pas le droit d’intervertir l’ordre des termes ; les équivalences impropres, où l’on peut changer l’ordre des termes, mais à condition d’en respecter l’ordre circulaire ; les homologies sans division où l’on peut intervertir cet ordre d’une manière quelconque et qu’on peut additionner, soustraire et multiplier ; enfin les homologies par division qu’on peut, en outre, diviser.

Quand il n’y aura pas d’avis contraire, et que nous parlerons d’une équivalence, il s’agira toujours d’une équivalence propre.

On peut se placer, dans l’étude de la question qui nous occupe, à plusieurs points de vue différents. Représentons d’abord notre surface par un polygone fuchsien $R_0$ de la première famille, construisons les différents transformés de ce polygone par les transformations du groupe fuchsien correspondant $G$ ; ces transformés rempliront le cercle fondamental. Un cycle quelconque $C$ sera alors représenté par un arc de courbe $MM'$, allant d’un point $M$ à un de ses transformés $M'$. Deux cycles proprement équivalents seront représentés par deux arcs de courbes $MPM'$ et $MQM'$ ayant mêmes extrémités et réciproquement deux arcs ayant mêmes extrémités représenteront deux cycles équivalents. Un arc $M_1 Q M_1'$ représentera un cycle improprement équivalent au cycle représenté par l’arc $MM'$, si la même substitution du groupe $G$ qui change $M$ en $M'$ change également $M_1$ en $M_1'$.

Soit un arc $MPM'$ représentant un cycle $C$ ; considérons les divers transformés de cet arc par les substitutions du groupe $G$ ; tous ces transformés représenteront également le cycle $C$. La condition pour que le cycle $C$ ne soit pas bouclé, c’est que l’arc $MPM'$ ne coupe aucun de ces transformés.

De même, soient $MPM'$, $M_1QM_1'$ deux arcs représentant deux cycles $C$ et $C'$ ; la condition pour que les deux cycles $C$ et $C'$ ne se coupent pas, c’est que l’arc $MPM'$ ne coupe ni l’arc $M_1QM_1'$ ni aucun de ses transformés.

Cela posé, cherchons si parmi les cycles improprement équivalents à $C$ il y en a qui ne soient pas bouclés ; reprenons l’arc $MPM'$ et la substitution $S$ du groupe $G$ qui change $M$ en $M'$. Cette substitution est hyperbolique ; en effet, dans le cas qui nous occupe, qui est celui d’un polygone $R_0$ de la première famille dont les sommets forment un cycle unique et dont la somme des angles est $4 \pi$ [1], toutes les substitutions de $G$ sont hyperboliques.

La substitution $S$ a donc deux points doubles $\alpha$ et $\beta$ sur le cercle fondamental.

Joignons ces deux points par une droite non euclidienne, c’est-à-dire, d’après la terminologie adoptée dans la théorie des fonctions fuchsiennes, par un cercle coupant orthogonalement le cercle fondamental. Soit $M_1$ un point quelconque de cette droite non euclidienne $\alpha \beta$, son transformé $M_1'$ par la substitution $S$ sera également sur cette droite $\alpha \beta$. Soit $M_1QM_1'$ l’arc de la droite non-euclidienne compris entre $M_1$ et $M_1'$. Il représentera un cycle improprement équivalent au cycle $MPM'$.

Considérons maintenant les transformés de $M_1QM_1'$ par les diverses transformations de $G$, ce seront aussi des arcs de droite non euclidienne. Les transformés par la substitution $S$ et ses multiples nous donneront la droite $\alpha \beta$ tout entière ; les autres transformés nous donneront d’autres droites non euclidienne [2], à savoir les droites $\alpha' \beta'$ qui joignent les deux points doubles $\alpha'$ et $\beta'$ [3] des diverses substitutions transformées de $S$ par les substitutions de $G$, c’est-à-dire des diverses substitutions hyperboliques $T^{-1} S T$, $T$ étant une transformation de $G$.

Le cycle $M_1 Q M_1'$ ne sera donc pas bouclé si ces diverses droites non euclidiennes ne se coupent pas ; et pour qu’elles ne se coupent pas, il faut et il suffit que pour aucune des substitutions $T^{-1} ST$, les deux points doubles $\alpha'$ et $\beta'$ ne se croisent sur le cercle fondamental avec les deux points doubles $\alpha$ et $\beta$, c’est-à-dire ne se présentent dans l’ordre circulaire $\alpha \alpha' \beta \beta'$ ou dans l’ordre inverse.

Réciproquement, je suppose que deux de nos droites non euclidiennes se coupent ; je dis que tous les cycles improprement équivalents à $MPM'$ seront bouclés. Si elles se coupent, en effet, c’est que les points doubles $\alpha, \beta$ et $\alpha', \beta'$ de $S$ et de $T^{-1} S T$ se croisent. Considérons un arc quelconque $M_2 M_2'$ improprement équivalent à $MPM'$ ; alors $M_2'$ est le transformé de $M_2$ par $S$ ; considérons d’abord les transformés de l’arc $M_2 M_2'$ par la substitution $S$ et ses multiples ; ils joindront entre eux les transformés successifs de $M_2$ par les multiples de $S$ ; ils formeront donc un trait continu qui ira de $\alpha$ en $\beta$.

Pour la même raison, les transformés de l’arc $M_2 M_2'$ par les substitutions $S^m T$ (où $m$ est un entier positif ou négatif), formeront un trait continu qui ira de $\alpha'$ en $\beta'$ ; comme les points $\alpha, \beta, \alpha', \beta'$ sont croisés, il faut que ces deux traits continues se coupent ; c’est-à-dire que deux des transformés de l’arc $M_2 M_2'$ se coupent, c’est-à-dire que le cycle $M_2 M_2'$ soit bouclé.

C.Q.F.D.

De même, soient $MPM'$ et $NQN'$ deux arcs représentant deux cycles fermés.

Parmi les cycles improprement équivalents à $MPM'$ et $NQN'$, y en a-t-il qui ne se coupent pas ? Soient $S$ et $S_1$ les substitutions qui changent $M$ en $M'$, et $N$ en $N'$. Soient $\alpha$ et $\beta$ les points doubles de $S$ ; $\alpha_1$ et $\beta_1$ les points doubles de $S_1$. Traçons les deux droites non euclidiennes $\alpha \beta$ et $\alpha_1 \beta_1$, prenons sur ces deux droites deux points quelconques $M_1$ et $N_1$ ; soit $M_1'$ le transformé de $M_1$ par $S$, et $N_1'$ celui de $N_1$ par $S_1$ ; le point $M_1'$ sera sur la droite $\alpha \beta$ et le point $N_1'$ sur la droite $\alpha_1 \beta_1$.

Considérons les arcs de droite non euclidienne, $M_1M_1'$ et $N_1 N_1'$ ; ils représenteront deux cycles improprement équivalents à $MPM'$ et à $NQN'$.

Par un raisonnement tout pareil à celui qui précède, on verrait que si les points doubles $\alpha$ et $\beta$ de $S$ ne se croisent pas avec les points doubles $\alpha_1$ et $\beta_1$ de $S_1$, ni avec les points doubles des diverses transformées $T^{-1} S_1 T$ de $S_1$, les cycles $M_1 M_1'$ et $N_1 N_1'$ ne se coupent pas ; et que si, au contraire, $\alpha$ et $\beta$ se croisent, soit avec $\alpha_1$ et $\beta_1$, soit avec les points doubles de l’une des transformées $T^{-1} S_1 T$, non seulement les cycles $M_1 M_1'$ et $N_1 N_1'$ se coupent, mais qu’il en est de même de deux cycles quelconques improprement équivalents à $MPM'$ et $NQN'$.

On peut encore présenter la chose sous une autre forme. Supposons que le cycle $M_1 M_1'$ ne soit pas bouclé ; alors la droite non euclidienne $\alpha \beta$ et ses diverses transformées ne se coupent pas ; ces droites non euclidiennes partageront alors la surface du cercle fondamental en une infinité de régions. Si le point $N$ appartient à l’une de ces régions et si le point $N'$ transformé de $N$ par $S_1$ appartient à une autre région, les cycles $M_1 M_1'$ et $NN'$ se couperont, ainsi que les cycles improprement équivalents ; si les deux points $N$ et $N'$ appartiennent à la même région, ces cycles ne se couperont pas.

Plaçons-nous maintenant à un autre point de vue. Envisageons un cycle $C$ représenté par un arc $MPM'$ et tous les transformés de cet arc. Le cycle sera bouclé si deux de ces transformés se coupent ; mais s’il existe une intersection de deux transformés, il y en aura une infinité qui se déduiront les unes des autres par les substitutions de $G$ et, en particulier, il y en aura une à l’intérieur de $R_0$.

Il suffira donc d’envisager les portions de l’arc $MPM'$ et de ses transformés qui sont à l’intérieur de $R_0$. Notre cycle sera alors représenté par un certain nombre d’arcs $A_i B_i$ qui iront d’un point du périmètre de $R_0$ à un autre point de ce périmètre.

Quand un point décrira sur la surface fermée $S$ le cycle fermé $C$ tout entier, le point correspondant sur $R_0$ décrira successivement les arcs

$$ A_1 B_1, A_2 B_2, \dotsc , A_n B_n .$$

Les points $A$ et $B$ appartiendront au périmètre de $R_0$, on sait que ce périmètre se compose d’un certain nombre de côtés conjugués deux à deux ; il est clair que les points $B_1$ et $A_2$, $B_2$ et $A_3, \dotsc, B_{n-1}$ et $A_n$, $B_n$ et $A_1$ doivent être conjugués.

Si les arcs $A_i B_i$ ne se coupent pas entre eux, le cycle n’est pas bouclé.

De même, si au lieu d’un cycle, nous en considérons deux ou plusieurs, et si les arcs représentatifs de ces divers cycles ne se coupent pas entre eux, ces divers cycles ne se couperont pas entre eux.

Supposons, pour fixer les idées, $p=2$. Alors le polygone $R_0$ est un octogone dont les côtés consécutifs représentent respectivement les cycles

$$ + C_1, + C_2, - C_1, - C_2, + C_3, + C_4, - C_3, - C_4, $$

ce qui montre d’abord que l’on a entre les quatre cycles fondamentaux l’équivalence

$$ \tag{26} C_1 + C_2 - C_1 - C_2 + C_3 + C_4 - C_3 - C_4 \equiv 0,$$

 [4] puisque le polygone $R_0$ est une aire simplement connexe.

Soit $M$ un point intérieur à $R_0$, $N$ un point situé sur un des côtés de $R_0$, et $N'$ le point correspondant sur le côté conjugué. Nous voyons tout de suite que le cycle $MN' + NM$ est improprement équivalent

$$ \tag{27} \left\{ \begin{array}{ccccc} \text{à} & + C_2 & \text{ si le point } N \text{ est sur le côté} & + C_1 \ ; \\ & - C_1 & \text{»} \quad \quad \quad \text{»} & + C_2 \ ; \\ & - C_2 & \text{»} \quad \quad \quad \text{»} & - C_1 \ ; \\ & + C_1 & \text{»} \quad \quad \quad \text{»} & - C_2 \ ; \\ & + C_4 & \text{»} \quad \quad \quad \text{»} & + C_3 \ ; \\ & - C_3 & \text{»} \quad \quad \quad \text{»} & + C_4 \ ; \\ & - C_4 & \text{»} \quad \quad \quad \text{»} & - C_3 \ ; \\ & + C_3 & \text{»} \quad \quad \quad \text{»} & - C_4. \\ \end{array} \right.$$

Cela posé, nous verrons que l’arc $A_i B_i$ est équivalent à l’arc $A_i M B_i$ ; par conséquent, notre cycle

$$C = A_1 B_1 + A_2 B_2 + \dotsc + A_n B_n$$

est équivalent à

$$ A_1 MB_1 + A_2 M B_2 + \dotsc + A_n M B_n$$

et, par conséquent, improprement équivalent à

$$ (MB_n + A_1 M) + (MB_1 + A_2 M) + \dotsc + (MB_{n-1} + A_n M).$$

Or l’une quelconque des expressions entre parenthèses, par exemple $MB_1 + A_2 M$, est analogue au cycle $MN' + NM$ dont nous venons de parler. Elle sera donc équivalente à l’un des cycles fondamentaux $\pm C_1, \pm C_2, \pm C_3, \pm C_4$ et pour savoir auquel de ces cycles, il suffira d’examiner sur quel côté de $R_0$ se trouve le point $A_i$ et de se reporter au tableau (27).

Nous voyons ainsi que notre cycle $C$ est improprement équivalent à une combinaison des cycles fondamentaux et nous avons le moyen de déterminer cette combinaison. La combinaison ainsi trouvée n’est pas la seule à laquelle $C$ soit équivalent, car nous pouvons transformer l’équivalence ainsi obtenue en nous servant de l’équivalence (26) qui est la seule qui ait lieu entre les cycles fondamentaux.

Inversement, étant donnée une combinaison $K$ quelconque des cycles fondamentaux, nous avons le moyen de former un cycle équivalent représenté par une série d’arcs $A_1 B_1, A_2 B_2, \dotsc, A_n B_n$.

Écrivons notre combinaison $K$, par exemple, sous la forme

$$ K = + C_1 + C_1 + C_2 - C_3 + C_4 + C_4 - C_1 - C_2 -C_2$$

ou sous une forme analogue ; chacun des termes de la combinaison sera un des cycles fondamentaux $C_i$ affecté du coefficient $+ 1$ ou $-1$. L’ensemble de deux termes consécutifs s’appellera une séquence et j’appellerai aussi séquence l’ensemble du dernier et du premier terme, de sorte qu’il y aura dans notre combinaison autant de séquences que de termes.

A chaque séquence correspondra un arc $A_i B_i$ ; le point $A_i$ se trouvera sur le côté

$$ + C_1, + C_2 , -C_1, -C_2 , + C_3 , + C_4, - C_3, - C_4$$

si le premier terme de la séquence est respectivement

$$ + C_2, -C_1, -C_2, +C_1, + C_4, - C_3, - C_4, + C_3, $$

et le point $B_i$ se trouvera sur le côté

$$ - C_1, - C_2, + C_1, + C_2, - C_3, -C_4, + C_3, + C_4$$

si le second terme de la séquence est respectivement

$$ + C_2, -C_1, -C_2, +C_1, + C_4, - C_3, - C_4, + C_3. $$

Deux arcs $A_i B_i$ et $A_k B_k$ se couperont forcément si les points $A_i B_i$ se croisent avec les points $A_k B_k$ sur le périmètre de $R_0$. Nous dirons alors que les deux séquences correspondantes sont incompatibles. Si, au contraire, ces quatre points ne se croisent pas, nous pourrons tracer les deux arcs de façon qu’ils ne se rencontrent pas.

Comment reconnaîtrons-nous si deux séquences sont incompatibles ; cela ne présentera aucune difficulté si les quatre points $A_i B_i A_k B_k$ sont sur quatre côtés différents ; l’ordre circulaire de ces quatre points sera celui des quatre côtés qui est connu.

Mais si, par exemple, $A_i$ et $A_k$ sont sur un même côté, il faut envisager deux séquences consécutives $A_{i-1}B_{i-1} + A_i B_i$ et $A_{k-1} B_{k-1} + A_k B_k$. Nous voulons que les points $A_{i-1} B_{i-1}$ et $A_{k-1} B_{k-1}$, d’une part ne se croisent pas et que les points $A_iB_i$ et $A_kB_k$ d’autre part ne se croisent pas non plus. Pour désigner un côté sur lequel se trouve un des points $A_i, \dotsc,$ nous emploierons cette même lettre $A_i$.

Par hypothèse, les points $A_i$ et $A_k$ se trouveront sur un même côté $A_i A_k$, et il en résulte que les points $B_{i-1}$ et $B_{k-1}$ se trouvent également sur un même côté $B_{i-1} B_{k-1}$ conjugué de $A_i A_k$.

Cela posé, parcourons le périmètre de $R_0$ de façon à rencontrer successivement les côtés $A_{i-1}, B_{i-1} B_{k-1}, A_{k-1}$ ; les points $A_{i-1} B_{i-1}$ et $A_{k-1} B_{k-1}$ ne devant pas être croisés, nous rencontrerons $B_{i-1}$ avant $B_{k-1}$.

Parcourons maintenant le périmètre de $R_0$ en sens contraire, [5] quand nous parcourrons le côté conjugué $A_i A_k$, nous devrons rencontrer $A_i$ avant $A_k$, puisque $A_i$ est conjugué de $B_{i-1}$, et $A_k$ de $B_{k-1}$ ; et comme les points $A_i B_i$ et $A_k B_k$ ne doivent pas être croisés, nous rencontrerons les côtés $B_i, A_iA_k$ et $B_k$ dans l’ordre que je viens d’indiquer.

Donc pour que les séquences soient compatibles, il faut que pour rencontrer successivement les côtés $A_{i-1}, B_{i-1} B_{k-1}, A_{k-1}$ ou bien pour rencontrer successivement les côtés $B_i, A_i A_k, B_k$ on doive parcourir $R_0$ dans deux sens opposés.

Les autres cas douteux se ramèneraient au précédent en renversant l’un des deux arcs $A_i B_i$ ou $A_k B_k$.

Cela posé, un cycle dont toutes les séquences sont compatibles sera équivalent à un cycle non bouclé ; un cycle qui aura des séquences incompatibles ne sera pas équivalent à un cycle non bouclé, à moins qu’on ne puisse faire disparaître ces séquences par le moyen de l’équivalence (26). On reconnaîtrait de la même manière si deux ou plusieurs cycles sont équivalents à des cycles qui ne se coupent pas.

L’application de ces règles nous apprend, par exemple, que de toutes les combinaisons des cycles impairs $C_1$ et $C_3$, les seules qui soient équivalentes à des cycles non bouclés sont les suivantes :

$$C_1, C_3, C_1 + C_3, C_3 + C_1.$$

Mais pour ce qui va suivre, j’ai besoin de me placer encore à un autre point de vue.

Représentons notre surface par un polygone fuchsien $R_0'$ de la troisième famille qui, pour $p=2$, sera limité extérieurement par un cercle et intérieurement par trois autres cercles. Construisons les divers transformés de $R_0'$ par les substitutions du groupe correspondant $G'$ ; ils rempliront cette fois le plan tout entier, sauf une infinité de points singuliers répartis sur la circonférence du cercle fondamental.

Un cycle sera encore représenté par un arc $MM'$ allant d’un point $M$ à l’un de ses
transformés $M'$.

Mais deux arcs ayant mêmes extrémités ne représenteront pas toujours deux cycles équivalents ; il faut, en outre, que dans l’aire comprise entre ces deux arcs, il n’y ait pas de point singulier. A part cela, ce que nous avons dit pour les polygones fuchsiens de la première famille subsiste.

Construisons les divers transformés de l’arc $MM'$ par les substitutions de $G'$ ; conservons ensuite les portions de ces transformés qui sont à l’intérieur de $R_0'$ ; notre cycle se trouvera alors représenté par une série d’arcs

$$A_1 B_1, A_2 B_2, \dotsc, A_n B_n$$

allant d’un point du périmètre de $R_0'$ à un autre point de ce périmètre, et tels que les points $B_{i-1}$ et $A_i, B_n$ et $A_1$ soient conjugués.

Pour qu’un cycle ne soit pas bouclé, ou pour que les deux cycles ne se coupent pas, la condition c’est que les arcs $A_i B_i$ qui représentent ce ou ces cycles ne se coupent pas ; et on le reconnaîtra par des moyens analogues à ceux que nous venons d’exposer.

Mais il nous reste une question à traiter. Étant donné un cycle représenté par un certain nombre d’arcs $A_i B_i$, à quelle combinaison des cycles fondamentaux est-il équivalent ?

Pour résoudre cette question, cherchons à revenir au cas du polygone de la première famille $R_0$.

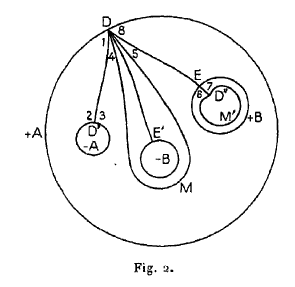
Notre polygone $R_0'$ est limité extérieurement par le cercle $+ A$ et intérieurement par le cercle $-A$ conjugué de $+ A$ et par les cercles $+ B$ et $- B$ conjugués l’un de l’autre. Je vais chercher à modifier $R_0'$ de façon à le transformer en un polygone $R_0''$ homéomorphe de $R_0$.

Soient $D$ et $D'$ deux points conjugués sur $+A$ et $-A$ ; soient $E$ et $E'$ deux points conjugués sur $+ B$ et $-B$. Joignons $DD', DE, DE'$ par des arcs de courbe qui seront regardés comme des coupures. Enveloppons la coupure $DE$ et le cercle $-B$ par une courbe fermée $DMD$ qui en reste très peu distante. Considérons la figure $DE'M$ comprise entre cette courbe fermée et $-B$ et sa transformée $D''EM'$ par la substitution de $G'$ qui change $-B$ en $+ B$. Retranchons du polygone $R_0'$ la figure $DE'M$ et annexons-lui, en revanche, la figure $D''EM'$, nous obtiendrons un nouveau polygone $R_0''$ qui représentera la surface fermée au même titre que $R_0'$ ; ce polygone sera limité extérieurement par le cercle $+ A$ et intérieurement par le cercle $-A$ et les courbes fermées $DMD$ et $D''M'D''$ ; mais ce polygone $R_0''$, grâce aux coupures $DD', DE, DE', D''E$ sera devenu simplement connexe ; les numéros $1, 2, ...$, à $8$ marqués sur la figure indiquent l’ordre dans lequel on rencontrera les sommets de ce polygone simplement connexe quand on en parcourra le périmètre. On voit, par l’ordre de conjugaison des côtés, que ce polygone est homéomorphe à $R_0$ et de telle façon qu’aux côtés de $R_0''$ [6]

$$ 81, \ 12, \ 23, \ 34, \ 45, \ 56, \ 67, \ 78$$

correspondent les côtés de $R_0$

$$+ C_1, + C_2, - C_1, - C_2, + C_3, + C_4, - C_3, -C_4.$$

Étant ainsi ramené au cas de $R_0$ il nous est aisé d’énoncer la règle.

A chacun des arcs $A_iB_i$ qui traversent $R_0'$ pourront correspondre plusieurs arcs analogues traversant $R_0''$, parce que l’arc primitif peut être partagé en plusieurs tronçons par les coupures. A chacun des arcs partiels traversant $R_0''$ correspondra, d’après la règle démontrée dans le cas de $R_0$, un terme et un seul dans la combinaison de cycles fondamentaux cherchée. A chacun de nos arcs primitifs $A_iB_i$ correspondra donc un ou plusieurs termes de cette combinaison.

Le premier de ces termes dépend de la position du point initial $A_i$ ; si ce point est sur les cercles

$$ + A, - A, + B, -B, $$

ce premier terme sera respectivement

$$ +C_2, - C_2, -C_4, + C_4.$$

Les termes suivants dépendent des coupures $DD', DE, DE'$ successivement rencontrées par l’arc $A_iB_i$ ; si cet arc rencontre en allant de gauche à droite

$$DD' \text{ ou } DE \text{ ou } DE',$$

les termes correspondants seront respectivement

$$ + C_1, + C_3, -C_4 - C_3 + C_4$$

et si ces coupures sont rencontrées de droite à gauche, ils seront

$$ -C_1, - C_3, -C_4 + C_3 + C_4.$$

Il est donc aisé, d’après cette règle, de former la combinaison cherchée.

Dans tout ce chapitre, je me suis placé au point de vue de l’équivalence impropre ; si l’on voulait déduire de là des théorèmes analogues pour l’équivalence propre, il suffirait d’observer que toute surface fermée est homéomorphe à elle-même de telle façon qu’un point quelconque $A$ de cette surface corresponde à un autre point quelconque de cette même surface.