§5 du cinquième complément

Envisageons, en particulier, une variété $V$ à trois dimensions définie comme au paragraphe 2 ; son squelette se réduira à un simple segment de droite le long duquel la variable que nous avons appelée $t$ variera de $0$ à $1$. Le système $W(t)$ se composera d’une variété unique ; cette variété sera une surface fermée ordinaire que nous supposerons bilatère, qui se réduira à un point pour $t=0$ et dont l’ordre de connexion ira sans cesse en croissant quand $t$ croîtra de $0$ à $1$ et sera égal à $2p+1$ pour $t=1$.

Il résulte de cette définition que la variété $V$ n’est pas fermée.

D’après ce que nous avons vu au paragraphe 2, la droite qui forme le squelette de $V$ sera subdivisée en tronçons par certaines valeurs remarquables de $t$.

Soient

$$t_1, t_2, \dotsc, t_p$$

ces valeurs remarquables ; ce seront celles pour lesquelles la surface $W(t)$ a un point singulier et, d’après nos hypothèses, celles pour lesquelles l’ordre de connexion de cette surface augmente de deux unités.

Ainsi $W$ sera $1$ fois connexe pour $t$ compris entre $0$ et $t_1$, $3$ fois pour $t$ compris entre $t_1$ et $t_2, \dotsc, 2q+1$ fois entre $t_q$ et $t_{q+1}, \dotsc,$ et enfin $2p+1$ fois entre $t_p$ et $1$.

La surface $W$ reste homéomorphe à elle-même tant que la variable $t$ reste sur un même tronçon.

Supposons que nous faisions décroître $t$ et que $t$ passe par une des valeurs remarquables ; il arrive alors comme nous l’avons vu au paragraphe 2 qu’un des cycles $C$ de la surface $S$ se réduit à un point ; que tous les cycles équivalents à $C$ deviennent équivalents à zéro et, d’autre part que tous les cycles qui rencontraient $C$ cessent d’exister.

C’est ainsi que le nombre des cycles réellement distincts, et par conséquent, l’ordre de connexion se trouve diminué de deux unités.

Nous allons maintenant définir le cycle $K_q$. Pour $t= t_q + \varepsilon$, il existe sur $W(t_q + \varepsilon)$ un cycle infiniment petit qui se réduit à un point pour $t=t_q$.

C’est ce cycle que j’appelle $K_q$. La surface $W(t)$ reste homéomorphe à elle-même quand $t$ varie de $t_q$ à $t_{q+1}$ ; [et l’on peut supposer que l’homéomorphisme est tel que pour deux valeurs infiniment voisines $t$ et $t'$, les deux points correspondants sur $W(t)$ et $W(t')$ soient infiniment peu différents l’un de l’autre]. La surface $W(t)$ reste donc homéomorphe à $W(t_q + \varepsilon)$ et au cycle $K_q$ correspondra sur $W(t)$ un cycle que j’appellerai encore $K_q$. Pour définir $K_q$ sur la surface $W(t_{q+1} + \varepsilon)$, il suffit de dire que ce cycle doit différer très peu du même cycle sur la surface $W(t_{q+1} - \varepsilon)$ ; comme $W(t)$ reste homéomorphe à elle-même pour toutes les valeurs de $t$ comprises entre $t_{q+1}$ et $t_{q+2}$, on peut définir comme plus haut le cycle $K_q$ pour ces valeurs de $t$, et ainsi de suite.

Le cycle $K_q$ étant ainsi défini, j’arrive à la propriété essentielle, à savoir que deux cycles $K_{\alpha}$ et $K_{\beta}$ ne se coupent pas. Soient $\beta > \alpha$, et soit d’abord $t = t_{\beta} + \varepsilon$ ; alors $K_{\beta}$ est très petit et je dis que $K_{\alpha}$ ne coupe pas $K_{\beta}$. En effet, d’après sa définition, le cycle $K_{\alpha}$ existe encore pour $t < t_{\beta}$, or j’ai dit que les cycles qui coupent le cycle très petit $K_{\beta}$ disparaissent quand $t$ devient $< t_{\beta}$. Faisons varier $t$ de $t_{\beta}$ à $t_{\beta + 1}$. Entre ces limites, toutes les surfaces $W(t)$ sont homéomorphes entre elles et comme sur l’une d’elles les cycles $K_{\alpha}$ et $K_{\beta}$ ne se coupent pas, les cycles correspondants $K_{\alpha}$ et $K_{\beta}$ ne se couperont sur aucune d’elles. Comme $K_{\alpha}$ et $K_{\beta}$ ne se coupent pas sur $W(t_{\beta +1} - \varepsilon)$, on conclura que sur la surface infiniment voisine $W(t_{\beta + 1} + \varepsilon)$, les deux cycles $K_{\alpha}$ et $K_{\beta}$ ne se couperont pas non plus ; pour $t_{\beta + 1} < t < t_{\beta + 2}$, toutes les surfaces $W(t)$ sont homéomorphes et comme sur l’une d’elles les cycles $K_{\alpha}$ et $K_{\beta}$ ne se coupent pas, ils ne se couperont sur aucune d’elles ; et ainsi de suite.

Donc les cycles $K_{\alpha}$ et $K_{\beta}$ ne se coupent pas.

C.Q.F.D.

J’ajoute que le cycle $K_q$ n’est pas bouclé ; il ne l’est pas pour $t = t_q + \varepsilon$ puisqu’il se réduit à une courbe fermée très petite ; donc à cause de l’homéomorphisme il ne l’est pas pour $t_q < t < t_{q+1}$ ; il ne l’est pas pour $t = t_{q+1} + \varepsilon$, parce qu’alors il diffère très peu de ce qu’il est pour $t = t_{q+1} - \varepsilon$ ; et ainsi de suite.

Faisons varier $t$ depuis $t_q$ jusqu’à $1$, le cycle $K_q$ variera d’une façon continue ; pour $t = t_q$ il se réduit à un point et pour $t > t_q$ à une courbe fermée unique. Il engendrera donc une aire simplement connexe que j’appelle $A_q$.

Deux aires $A_{\alpha}$ et $A_{\beta}$ n’ont aucun point commun ; et, en effet, s’ils [1] en avaient un, ce point appartiendrait à une surface $W(t)$ et sur cette surface aux deux cycles $K_{\alpha}$ et $K_{\beta}$ ; or nous venons de voir que ces deux cycles ne se coupent pas.

Désignons encore par $B_q$ l’aire partielle engendrée par $K_q$ quand $t$ varie depuis $t_q$ jusqu’à $t \ (t < 1)$ et qui, comme $A_q$, est simplement connexe. Nous allons traiter $K_q, A_q$ et $B_q$ comme des coupures ; à cet effet, considérons deux cycles $K_q'$ et $K_q''$ infiniment peu différents de $K_q$ ; nous pouvons supposer que ces deux cycles ne se coupent pas. La portion très petite de la surface $W(t)$ comprise entre ces deux cycles s’appellera $S_q(t)$. Les deux cycles $K_q'$ et $K_q''$ engendreront deux aires $A_q'$ et $A_q''$ quand $t$ variera de $t_q$ à $1$ et deux aires $B_q'$ et $B_q''$ quand $t$ variera de $t_q$ à $t$.

Cela posé, retranchons de la surface fermée $W(t)$ les aires très petites

$$S_1(t), S_2(t), \dotsc, S_p(t).$$

Après cette opération, la surface restante $W - \Sigma S_q$ ne sera plus une surface fermée, elle admettra pour frontière les $2p$ courbes fermées $K_q'$ et $K_q''$.

Ajoutons ensuite à cette surface les aires $B_q'$ et $B_q''$ ; le résultat de cette addition sera une surface

$$W_1(t) = W - \Sigma S_q + \Sigma B_q' + \Sigma B_q''$$

qui sera fermée puisque $B_q'$ admet $K_q'$ comme frontière complète et que $B_q''$ admet $K_q''$.

Je dis que la surface $W_1(t)$ ainsi obtenue est simplement connexe et sans singularité. Elle n’a pas de singularité, parce que ses différentes parties ne se coupent pas et n’ont d’autres points communs que ceux des courbes $K_q'$ et $K_q''$ qui leur servent de frontières. Et, en effet, $W(t)$ ne peut avoir aucun point commun avec $B_q'$ ou $B_q''$, en dehors de $K_q'$ et $K_q''$ ; et, d’autre part, comme les aires $B_{\alpha}$ et $B_{\beta}$ ne se coupent pas, les aires $B_q', B_q'', B_{\alpha}', B_{\alpha}'', \dotsc$, n’auront non plus aucun point commun.

D’autre part, la surface non fermée $W - \Sigma S_q$ est homéomorphe à une aire plane limitée extérieurement par une courbe fermée et intérieurement par $2p -1$ autres courbes fermées (cela n’est pas autre chose que la représentation de la surface $W$ par un polygone fuchsien de la troisième famille dont il a été question plus haut au paragraphe 3) ou, ce qui revient au même, à une aire sphérique, comprenant [2] ce qui reste d’une sphère quand on en a retranché $2p$ petites aires $\alpha$ simplement connexes et extérieures les unes aux autres.

D’un autre côté, les $2p$ aires $B'$ et $B''$ peuvent être considérées comme homéomorphes aux $2p$ aires $\alpha$ ; on verra ainsi, en faisant attention à la façon dont se fait le raccordement, que la surface totale

$$W_1 = W - \Sigma S + \Sigma B' + \Sigma B''$$

est homéomorphe à la sphère entière, c’est-à-dire simplement connexe.

C.Q.F.D.

Faisons varier maintenant $t$ depuis $0$ jusqu’à $1$, et en même temps imaginons que les cycles $K_q'$ et $K_q''$ se rapprochent de $K_q$ de façon à se confondre avec $K_q$ pour $t=1$.

Je suppose que les positions successives de $K_q'$ et de $K_q''$ n’aient aucun point commun, pas plus par conséquent que les positions successives des aires $A_q'$ et $A_q''$, $B_q'$ ou $B_q''$. Dans ces conditions, tout point intérieur à $V$ (les points des aires $A_q$ exceptés) appartiendra à l’une des surfaces $W_1$ et à une seule. Les points de la surface limite $W(1)$ appartiendront à $W_1(1)$. Pour $t=1$, les aires $B_q'$ et $B_q''$ se réduiront à $A_q'$ et $A_q''$, et celles-ci elles-mêmes se réduiront aux aires $A_q$ puisque pour $t=1$ les cycles $K_q'$ et $K_q''$ se réduisent à $K_q$.

Si nous considérons donc un point de $A_q$, ce point se trouvera encore sur $W_1(1)$ mais à ce point de $A_q$ correspondront deux points de $W_1(1)$, l’un de ces points devant être considéré comme appartenant à $B_q' = A_q'$ et l’autre à $B_q'' = A_q''$.

Les surfaces simplement connexes $W_1(t)$ s’emboîtant mutuellement engendreront (cf. §1) une variété simplement connexe.

On peut donc dire qu’en pratiquant dans $V$ les $p$ coupures $A_q$ on rend cette variété simplement connexe. Pratiquons ces $p$ coupures, et déformons notre variété de façon à écarter les deux lèvres de ces coupures ; la variété nouvelle $U$ ainsi obtenue sera simplement connexe, limitée par une surface simplement connexe $H$ homéomorphe à une sphère. Sur cette surface simplement connexe nous distinguerons $2p$ aires simplement connexes qui seront les deux lèvres des $p$ coupures, et que j’appellerai les cicatrices ; ces cicatrices seront conjuguées deux à deux.

A chaque point de $U$ correspondra un point de $V$ et un seul ; de même à chaque point de $V$ correspondra un point de $U$ et un seul, sauf pour les points des aires $A_q$ à chacun desquels correspondront deux points de $U$ situés sur deux cicatrices conjuguées.

Considérons deux variétés analogues à $U$ ; chacune d’elles sera simplement connexe, chacune d’elles sera limitée par une surface simplement connexe portant $2p$ cicatrices simplement connexes conjuguées deux à deux et extérieures les unes aux autres. Il est clair que les deux figures ainsi formées seront homéomorphes entre elles et homéomorphes à la figure formée par une sphère dont la surface porte $2p$ cicatrices constituées par des petits cercles extérieurs les uns aux autres.

D’où cette conséquence importante ; toutes les variétés engendrées comme $V$ et pour lesquelles le nombre entier appelé plus haut $p$ est le même sont homéomorphes entre elles.

Supposons que dans l’espace ordinaire on construise une surface fermée $2p + 1$ fois connexe et sans singularité. Cette surface partagera l’espace en deux régions, l’une intérieure et l’autre extérieure. Soit $R$ la région intérieure. C’est une variété non
fermée à trois dimensions susceptible de la même génération que $V$. Donc $V$ est homéomorphe à $R$ pourvu que le nombre $p$ soit le même.

Donc, si j’appelle développables les variétés non fermées qui sont homéomorphes à une portion de l’espace plan, toutes les variétés engendrées comme $V$ sont développables.

On peut en tirer en passant une conséquence ; considérons dans l’espace ordinaire deux surfaces fermées $S$ et $S'$, l’une et l’autre $2p + 1$ fois connexes.

Soit $R$ le volume intérieur à $S$, et $R'$ le volume intérieur à $S'$. On sait que les deux surfaces $S$ et $S'$ sont homéomorphes ; mais l’on pourrait se demander s’il en est de même des deux volumes $R$ et $R'$ et au premier abord on pourrait être tenté de répondre négativement à cette question. On pourrait se représenter les diverses nappes de la surface $S'$ s’enchevêtrant les unes dans les autres d’une façon compliquée et formant des nœuds qu’il serait impossible de dénouer sans sortir de l’espace à trois dimensions. Loin de là, nous sommes maintenant en état de conclure que les deux volumes $R$ et $R'$ sont toujours homéomorphes, puisque ces deux volumes peuvent être engendrés comme $V$, et deux variétés engendrées comme $V$ sont toujours homéomorphes.

J’arrive maintenant à une question importante pour ce qui va suivre. Je reprends la variété $V$ limitée par la surface $W(1)$, et engendrée par la surface $W(t)$.

La même variété pourrait-elle être engendrée par une autre surface $W(t)$, qui comme $W(t)$ se réduirait à un point pour $t=0$, aurait un ordre de connexion constamment croissant et finalement se réduirait à $W(1)$ pour $t=1$ ? Il est évident que $V$ est susceptible d’une infinité de manières d’une pareille génération.

Je désignerai par $K_1', \dotsc, K_p'$ les $p$ cycles qui jouent dans la nouvelle génération le même rôle que les cycles $K_1, \dotsc, K_p$ dans l’ancienne.

Quelle relation y a-t-il entre les cycles $K$ et $K'$ ? Peut-on choisir arbitrairement les cycles $K'$, et quelles conditions doivent remplir $p$ cycles de la surface $W(t)$ pour pouvoir être choisis pour jouer le rôle des cycles $K'$ ?

1° Ces cycles ne doivent pas être bouclés ; 2° Ils ne doivent pas se couper.

Mais ce n’est pas tout. Le cycle $K_q$, par rapport à la variété $V$, est équivalent à zéro, puisqu’il forme la frontière complète de l’aire $A_q$ qui fait partie de $V$. Nous aurons donc les équivalences

$$\tag{1} K_1 \equiv K_2 \equiv \dotsc \equiv K_q \equiv 0 \quad(\textrm{mod}\, V)$$

et toutes celles qui s’en déduisent. Je dis que nous n’en aurons pas d’autres.

Je veux dire par là que si nous avons par rapport à $V$ une équivalence de la forme suivante :

$$ \tag{2} C \equiv 0 \quad(\textrm{mod}\, V),$$

$C$ étant un cycle de la surface frontière $W(1)$, que j’appellerai pour abréger $W$, nous aurons, par rapport à cette surface frontière $W$ une équivalence de la forme

$$ \tag{3} C \equiv - \alpha_1 + \beta_1 + \alpha_1 - \alpha_2 + \beta_2 + \alpha_2 - \dotsc - \alpha_n + \beta_n + \alpha_n \quad(\textrm{mod}\, V), $$

où les $\alpha_i$ sont des cycles quelconques de $W$ et où les $\beta_i$ sont des cycles de cette surface tels que

$$ \beta_i \equiv m K \quad(\textrm{mod}\, V)$$

$m$ étant un entier positif ou négatif et $K$ l’un des cycles $K_1, K_2, \dotsc, K_q$ ; et, en effet, si l’équivalence (3) a lieu, on aura a fortiori

$$ C \equiv \Sigma( - \alpha + \beta + \alpha)\quad(\textrm{mod}\, V)$$

ou, à cause des équivalences (1) qui entraînent $\beta \equiv 0$

$$C \equiv \Sigma(- \alpha + \alpha) \equiv 0 \quad(\textrm{mod}\, V).$$

L’équivalence (2) est donc une conséquence des équivalences (1).

Pour établir la proposition énoncée, je suppose que l’équivalence (2) ait lieu ; elle signifie que le cycle $C$ est la frontière complète d’une certaine aire simplement connexe $D$ située dans $V$.

Cette aire pourra couper l’aire $A_q$ suivant une ligne $L_q$ qui ira d’un point de $C$ à un autre point de $C$, puisque les extrémités de $L_q$ ne peuvent se trouver que sur la frontière de $A_q$ c’est-à-dire sur $W$, ou puisqu’elles sont sur $D$, sur l’intersection de $W$ et de $D$, c’est-à-dire sur $C$. L’aire $D$ pourra aussi ne pas couper $A_q$, ou la couper suivant plusieurs lignes distinctes $L_q$. Dans tous les cas les différentes lignes $L$ ne se couperont pas puisque les diverses aires $A$ ne se coupent pas et puisqu’on peut toujours supposer que les aires $A$ et $D$ n’ont pas de singularité et déformer au besoin un peu $D$ de façon que les surfaces $D$ et $A$ ne se touchent pas.

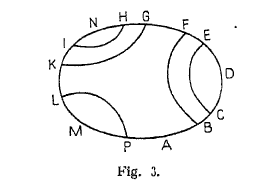
Chacune des lignes $L$ partage l’aire $D$ en deux parties puisque cette aire est simplement connexe. Cette aire $D$ sera donc divisée par les diverses lignes $L$ en un certain nombre d’aires partielles $\Delta_1, \Delta_2, \dotsc$. On peut parcourir successivement les contours des diverses aires partielles $\Delta$ de la façon suivante que je ferai mieux comprendre par un exemple que par des explications.

Sur la figure le cycle $ABCDEFGHNIKLMPA$ est le cycle $C$ ; les lignes $CE, BF, GK, HI, LP$ sont les lignes $L$.

Il est clair que le cycle total peut être remplacé par la somme des arcs suivants :

$$ \tag{4} \Sigma = \left\{ \begin{array}{l} (ABCDE + ECBA) + (ABCE + EF + FBA) \\ \ + (ABF + FGH + HNI + IHGFBA) \\ \ + (ABFGHI + IK + KGFBA) \\ \ + (ABFGK + KL + LPA) + (APL + LMP + PA). \end{array} \right. $$

On voit, en effet, que le dernier terme de chaque parenthèse est détruit par le premier terme de la parenthèse suivante et qu’en supprimant les termes ainsi détruits on retrouve le cycle total $C$.

Prenons maintenant l’une de ces parenthèses, la troisième par exemple ; elle peut s’écrire

$$ ABFGH + HNIH + HGFBA.$$

On voit que le premier et le dernier terme représentent un même arc $ABFGH$ parcouru une fois dans le sens direct, une fois dans le sens inverse, et que le second terme représente le contour de l’une des aires partielles $\Delta$, à savoir de l’aire $HIN$ ; il en est de même pour les autres parenthèses de l’expression [3] $\Sigma$ qui peut s’écrire

$$ \tag{5} \Sigma = \left\{ \begin{array}{l} (ABC + CDEC - CBA) + (AB + BCEFB + BA) \\ \ + (ABFGH + HNIH + HGFBA) \\ \ + (ABFG + GHIKG + GFBA) + (ABFGKLPA) + (AP + PLMP + PA). \end{array} \right. $$

Je vais encore modifier le chemin $\Sigma$. Ce chemin se compose d’arcs faisant partie du contour primitif $C$ et d’arcs formés par les lignes $L_q$. Ces derniers arcs se détruisent comme on l’a vu parce que dans l’expression (4) le dernier terme de chaque parenthèse est détruit par le premier terme de la suivante. Nous pouvons transformer ces derniers arcs ; nous remplacerons la ligne $L_q$ par un arc appartenant au cycle $K_q$ et ayant mêmes extrémités. Cela est possible parce que les deux extrémités de la ligne $L_q$ sont sur le cycle $K_q$ ; cela est permis d’ailleurs parce que ces nouveaux arcs, mis à la place des anciens, se détruiront, comme se détruisaient les anciens. Et si j’appelle $\Sigma'$ ce que devient le chemin $\Sigma$ après cette transformation, le cycle primitif $C$ peut donc aussi bien être considéré comme identique au chemin $\Sigma'$ qu’au chemin $\Sigma$.

Ce chemin $\Sigma'$ pourra être mis comme $\Sigma$ sous la forme (5) ; il suffit simplement d’admettre que, dans le second membre de (5), $CE$ par exemple représente, non la ligne $L_q$ qui a pour extrémités $C$ et $E$, mais l’arc du cycle $K_q$ qui va de $C$ en $E$.

L’avantage de cette transformation c’est que tous les points du chemin $\Sigma$ sont sur la surface limite $W$, tandis qu’il n’en aurait pas été de même de tous les points du chemin $\Sigma$.

Revenons à la variété simplement connexe $U$ définie plus haut.

Cette variété a pour frontière une surface simplement connexe que nous avons appelée $H$ et qui porte $2p$ cicatrices. Les parties de $H$ extérieures aux cicatrices correspondent alors à la surface $W$ et les cicatrices, comme nous l’avons vu, aux aires $A_q$.

Un contour fermé quelconque $Q$ tracé sur cette surface $K$ et restant en dehors des cicatrices sera équivalent à zéro par rapport à la variété $V$, en vertu des équivalences (1). En effet, ce contour enveloppera un certain nombre de cicatrices ; supposons pour fixer les idées qu’elle enveloppe deux cicatrices $A_1$ et $A_2$. Soit $M$ le point initial et final du contour fermé $Q$ ; soient, de même $M_1$ et $M_2$ les points initiaux et finaux des deux contours fermés $K_1$ et $K_2$ qui servent respectivement de périmètre aux deux cicatrices $A_1$ et $A_2$.

Joignons $M$ à $M_1$ et à $M_2$ par deux arcs $MM_1$ et $MM_2$ ; on aura

$$Q \equiv MM_1+K_1+M_1M+MM_2+K_2+M_2M \quad(\textrm{mod}\,W)$$

puisque la partie de la surface $H$ comprise entre les contours $Q,K_1$ et $K_2$ appartient à cette région de $H$ qui correspond à $W$.

Mais en vertu des équivalences (1)

$$K_1 \equiv K_2 \equiv 0 \quad(\textrm{mod}\, V):$$

donc

$$Q \equiv MM_1+M_1M + MM_2 + M_2M \equiv 0 \quad(\textrm{mod}\, V)$$

et cela a lieu comme je l’avais annoncé en vertu des équivalences (1).

Or, si nous envisageons le second terme de chaque parenthèse dans l’expression (5) du chemin $\Sigma'$, ce second terme représente sur $W$ un contour fermé ; il représentera également sur $H$ un contour fermé ; cela n’est pas évident et cela ne serait pas vrai pour un contour fermé de $W$ qui rencontrerait l’un des cycles $K_q$ ; à chaque point de $K_q$ correspond sur $U$ deux points distincts, de telle façon que quand un chemin continu sur $W$ rencontre $K_q$, le chemin correspondant sur $U$ saute brusquement d’un de ces deux points à l’autre et devient discontinu. Mais ici cette circonstance ne peut se présenter puisque le contour fermé que nous envisageons ne franchit jamais $K_q$ et se borne à le longer.

Le second terme de chaque parenthèse est donc équivalent à zéro en vertu des équivalences (1).

C.Q.F.D.

Nous pouvons donc ajouter une troisième condition à celles qui, nous l’avons vu, sont nécessaires pour que $p$ cycles de $W$ puissent être choisis pour jouer le rôle des cycles $K'$.

Le système des équivalences

$$K'_1\equiv K'_2 \equiv \ldots \equiv K'_p \equiv 0$$

ne doit pas différer du système des équivalences

$$K_1\equiv K_2 \equiv \ldots \equiv K_p \equiv 0,$$

de sorte que chacun de ces systèmes doit être une conséquence de l’autre.

Ces trois conditions sont-elles suffisantes ?

Soient $K'_1, K'_2, \ldots, K'_p,$ $p$ cycles non bouclés, ne se coupant pas mutuellement et tels que l’on ait

$$K'_1\equiv K'_2 \equiv \ldots \equiv K'_p \equiv 0 \quad(\textrm{mod}\, V).$$

L’équivalence $K'_q \equiv 0$ nous montre qu’il existe une aire $A'_q$ simplement connexe et dont la frontière complète est $K'_q$. Je dis que l’on peut toujours supposer que les diverses aires $A'_q$ n’ont aucun point commun.

Imaginons, en effet, que $A'_1, A'_2, \ldots, A'_{q-1}$ ne se coupent pas, mais qu’une ou plusieurs de ces $q-1$ aires soit coupée par $A'_q$. Soit $E_i$ l’intersection de l’aire $A'_q$ et de l’aire $A'_i$ ; cette intersection n’aura aucun point sur $K'_q$, puisque $K'_q$ ne pourrait rencontrer $A'_i$ que sur $W$ et, par conséquent, sur $K_i'$ et que $K_i'$ ne rencontre pas $K'_q$ par hypothèse. Cette intersection est donc tout entière à l’intérieur de $A'_q$ ; nous pouvons supposer que la surface $A'_i$ n’a pas de singularité et n’est pas tangente à la surface $A'_q$, sans quoi il suffirait de la déformer légèrement ; il en résulte que notre intersection est une courbe sans point double, elle doit donc se composer de plusieurs courbes fermées ne se coupant pas mutuellement.

De plus, l’intersection de $A'_i$ avec $A'_q$ ne coupera pas celle de $A'_k$ avec $A'_q$ (si $i$ et $k$ sont $

Les diverses intersections $E_i$ et $E_k$ se composeront donc d’un certain nombre de courbes fermées n’ayant aucun point commun. Si nous envisageons deux de ces courbes, ou bien elles seront extérieures l’une à l’autre, ou bien l’une d’elles sera intérieure à l’autre ; ces mots extérieur ou intérieur doivent s’entendre par rapport à l’aire simplement connexe $A'_q$. Parmi nos courbes fermées nous ne conserverons que celles qui ne sont intérieures à aucune autre ; elles seront alors toutes extérieures les unes aux autres. Soit $h_i$ l’une des courbes fermées conservées, appartenant à $E_i$. Cette courbe $h_i$ limitera une portion de l’aire simplement connexe $A'_q$ que j’appellerai $G_i$ et qui sera elle-même simplement connexe ; de même elle limitera une portion de l’aire simplement connexe $A'_i$ que j’appellerai $M_i$ et qui sera elle-même simplement connexe.

Nous pourrons tracer sur $A'_q$ une courbe fermée $h'_i$ à la quelle $h_i$ sera intérieure et qui différera très peu. Alors $h'_i$ limitera une portion de l’aire $A'_q$ que j’appellerai $G'_i$ et qui sera simplement connexe ; de même $h'_i$ limitera une aire simplement connexe $M'_i$ qui différera infiniment peu de $M_i$ et qui ne coupera pas l’aire $A'_i$.

Formons alors une aire $A''_q$ en enlevant de $A'_q$ toutes les aires $G'_i$ et en y ajoutant les aires $M_i'$

$$A''_q=A'_q + \sum M'_i - \sum G'_i.$$

On voit que $A''_q$ sera comme $A'_q$ une aire simplement connexe limitée par $K'_q$ puisqu’on remplace l’aire $G'_i$ par une autre aire simplement connexe limitée également par $h_i'$. Mais l’aire $A''_q$ ne coupera ni $A'_1$, ni $ A'_2$, \ldots, ni $A'_{q-1}$.

Nous pouvons donc supposer que les $q$ premières aires $A'_i$ ne se coupent pas, et en continuant de la sorte on verrait qu’on peut supposer que deux quelconques des $p$ aires $A'_i$ ne se coupent pas. C’est ce que nous ferons.

Un raisonnement analogue montrerait que les cycles $K'$ n’étant pas bouclés on peut toujours supposer que les aires $A'_i$ sont des surfaces sans courbe double.

Je me propose maintenant d’établir que les cycles $K'$ qui satisfont aux trois conditions énoncées peuvent jouer le rôle des cycles $K$, c’est-à-dire : 1° que $V$ peut être engendré par une surface $W'(t)$ qui se réduit à un point pour $t=0$ et à $W$ pour $t=1$, et qui pour $t_q < t < t_{q+1}$ est $2q+1$ fois connexe ; 2° que pour $t_q < t < t_{q+1}$, $W(t)$ coupe les aires $A'_1, A'_2, \ldots, A'_q$ suivant une seule courbe fermée et ne coupe pas les aires $A'_{q+1}, A'_{q+2}, \ldots, A'_p$ .

Je suppose que cela ait été démontré pour une variété développable, c’est-à-dire homéomorphe à une portion de l’espace plan ordinaire et limitée par une surface $2p-1$ fois connexe et je me propose de le démontrer pour une variété $V$ développable et limitée par une surface $W$ de connexion $2p+1$.

Pratiquons dans $V$ la coupure $A'_p$ et déformons légèrement cette variété après avoir séparé les deux lèvres de la coupure ; nous obtiendrons une nouvelle variété développable $V_1$ limitée par une surface $2p-1$ fois connexe ; cette surface $W_1$ se composera de deux parties, dont l’une correspond à la surface $W$ dans laquelle a été pratiquée la coupure $K'_p$, et l’autre est formée par deux cicatrices correspondant aux deux lèvres de la coupure.

Nous pouvons particulariser cette variété développable $V_1$ et cette surface $W_1$ de la façon suivante. Considérons un point intérieur à $V$ et soit $\delta$ la plus courte distance de ce point à la surface limite $W$ ou à la coupure $A'_p$. Les points tels que $\delta > \epsilon$ ($\epsilon$ petit) formeront le domaine $V_1$ ; les points tels que $\delta = \epsilon$ formeront la surface $W_1$ ; les points tels que $\delta < \epsilon$ formeront le domaine $V \setminus V_1$. On voit aisément que la surface $W_1$ est $2p-1$ fois connexe, et qu’elle est homéomorphe à la frontière du domaine obtenu en pratiquant dans $V$ la coupure $A'_p$.

La surface $W_1$ ne coupera pas l’aire $A'_p$, et coupera chacune des autres aires $A'_q$ suivant un cycle $K''_q$ peu différent de $K'_q$. Ces cycles $K''_q$ ne seront pas bouclés, ils ne se couperont pas mutuellement. De plus, le cycle $K''_q$ découpera dans l’aire simplement connexe $A'_q$ un domaine $A''_q$ simplement connexe dont il sera la frontière complète. Ce domaine $A''_q$ est la portion commune de $A'_q$ et de $V_1$ ; cela montre que $K''_q \equiv 0$ par rapport à $V_1$. Cela montre que les cycles $K''$ satisfont par rapport à $V_1$ aux conditions du théorème ; or le théorème est supposé démontré pour $V_1$.

Donc $V_1$ peut être engendré par une surface $W'(t)$ qui pour $t=0$ se réduit à un point, pour $t=u$ (où $t_{p-1}

Envisageons maintenant le domaine $V \setminus V_1$ limité extérieurement par la surface $W$ qui est $2p+1$ fois connexe et intérieurement par la surface $W_1$ qui est $2p-1$ fois connexe et qui ne coupe pas l’aire $A'_p$, laquelle se trouve tout entière à l’intérieur de $V \setminus V_1$. Il est clair que nous pourrons prendre sur $A'_p$ un point $M$ et construire une surface $W_2$ tout entière intérieure à $V \setminus V_1$, admettant ce point $M$ comme point conique et n’ayant aucun autre point commun avec $A'_p$, puis engendrer le domaine $V \setminus V_1$ par une surface $W'(t)$ qui pour $t=u$ se réduit à $W_1$ ; qui pour $u

Nous voyons que la variété $V$ pourra être engendrée par une surface $W'(t)$ satisfaisant à l’énoncé du théorème ; le théorème est donc démontré et les trois conditions énoncées sont non seulement nécessaires, mais suffisantes.

Il y a plus ; pour démontrer le dernier théorème, je me suis appuyé seulement sur ce fait que les équivalences $K' \equiv 0$ sont une conséquence des équivalences $K \equiv 0$ et je n’ai pas eu à m’appuyer sur le fait inverse, que les équivalences $K \equiv 0$ sont une conséquence des équivalences $K' \equiv 0$. Donc si les cycles $K'$ ne sont pas bouclés et ne se coupent pas mutuellement et si les équivalences $K \equiv 0$ entraînent les équivalences $K' \equiv 0$, inversement les équivalences $K' \equiv 0$ entraîneront les équivalences $K \equiv 0$. C’est ce qu’on pourrait vérifier directement.