Commentaires sur le §3 du cinquième complément

On peut découper ce §3 en quatre parties :

• de Avant d’aller plus loin à en polygones congruents : forme d’intersection, réduction dans une base adaptée construite à l’aide d’une fonction de Morse, assimilation de la surface à un polygone fuchsien (de deux types différents) ;
• de mais ici à homéomorphes l’une à l’autre : rappels sur l’homologie et l’homotopie sur les surfaces, dans différents modes de représentations (point de vue du revêtement universel et des lacets) ;
• de Mais on peut aller plus loin à relative aux cycles $C'$ : les automorphismes de $H_1(\Sigma_p,\mathbb{Z})$ qui sont induits par un homéomorphisme de la surface sont exactement ceux qui préservent la forme d’intersection, i.e. dont la matrice dans la base de réduction $([C_1],[C_3],...,[C_{2p-1}],[C_2],[C_4],...,[C_{2p}])$ appartient à $Sp(2p, \mathbb{Z})$ ;
• de Il est aisé de conclure à la fin : « corollaire » de ce qui précède : un élément du $H_1(\Sigma_p,\mathbb{Z})$ admet pour représentant une courbe fermée simple si et seulement si il est primitif, c’est-à-dire si et seulement s’il est combinaison des cycles fondamentaux avec des coefficients premiers entre eux.

Nos commentaires portent sur les premier, troisième et quatrième points du découpage ci-dessus.

Forme d’intersection et construction d’une base de réduction à l’aide d’une fonction de Morse

Poincaré commence par rappeler que pour une surface orientable de genre $p$, $\Sigma_p$, le nombre d’intersection définit une forme bilinéaire antisymétrique non dégénérée [1] $F$ sur $H_1(\Sigma_p,\mathbb{Z})$. Une telle forme possède toujours une base dans laquelle sa matrice est diagonale par blocs de la forme $\begin{pmatrix}0&1\\-1&0\end{pmatrix}$. Poincaré explique comment trouver concrètement une telle base dans le cas particulier de la forme d’intersection, à l’aide d’une fonction de Morse sur $\Sigma_p$ [2] (cf. nos commentaires du §2).

Formons le squelette de notre surface ; ce squelette sera un réseau où l’on pourra décrire $p$ chemins fermés distincts ; en choisissant convenablement $p$ points sur ce réseau, les $p$ chemins fermés seront coupés, le réseau restant néanmoins d’un seul tenant. Chacun de ces points représentera une courbe fermée qui sera la variété $w(t)$ du paragraphe précédent. Nous aurons donc $p$ courbes fermées qui n’auront aucun point commun et seront nos $p$ cycles

$$ C_1 , C_3 , \ldots , C_{2p-1} . $$

Découpons notre surface suivant ces $p$ courbes ; elle reste d’un seul tenant, mais elle peut maintenant être développée sur un plan et, après le développement elle se réduira à une aire plane limitée par $2p$ courbes fermées. Une de ces $2p$ courbes la limite extérieurement et les autres intérieurement. Ces $2p$ courbes sont conjuguées deux à deux, deux courbes conjuguées correspondant aux deux lèvres d’une même coupure.

Autrement dit, la fonction de Morse nous fournit $p$ courbes fermées simples $C_1,C_3,\dots,C_{2p-1}$ telles que, si l’on découpe $\Sigma_p$ le long de ces cycles, on obtient une sphère à $2p$ trous, ou, de manière équivalente, un disque à $2p-1$ trous. Ces courbes $C_1,C_3,\dots,C_{2p-1}$ sont en bijection avec les cycles du squelette associé à la fonction de Morse. L’animation suivante illustre cette construction dans le cas $p=2$. Les « cycles » $C_1$ et $C_3$ sont les courbes rouge et jaune respectivement.

Poincaré oublie d’expliquer comment on complète la famille $C_1,C_3,\dots,C_{2p-1}$ en une base $C_1,C_2,C_3,\dots,C_{2p}$ du premier groupe d’homologie de $\Sigma_p$. C’est très facile ! Dans la sphère à $2p$ trous obtenue ci-dessus, on choisit $p$ arcs deux à deux disjoints, chacun de ces arcs reliant les deux « lèvres » d’une même « coupure ». Par construction, les $p$ courbes fermées $C_2,\dots,C_{2p}$ obtenues à partir de ces arcs par identification des lèvres conjuguées complètent $C_1,C_3...,C_{2p-1}$ en un « système fondamental » de courbes $C_1, C_2,...,C_{2p}$ dont les classes d’homologie forment une base de $H_1(\Sigma_p ,\mathbb{Z})$ dans laquelle la forme d’intersection $F$ est de la forme voulue (si on les a orientés convenablement), i.e. est diagonale par blocs de la forme $\begin{pmatrix}0&1\\-1&0\end{pmatrix}$. La figure ci-dessous montre la construction des courbes $C_2$ et $C_4$ (en bleu clair et bleu foncé respectivement) dans l’exemple déjà considéré précédemment.

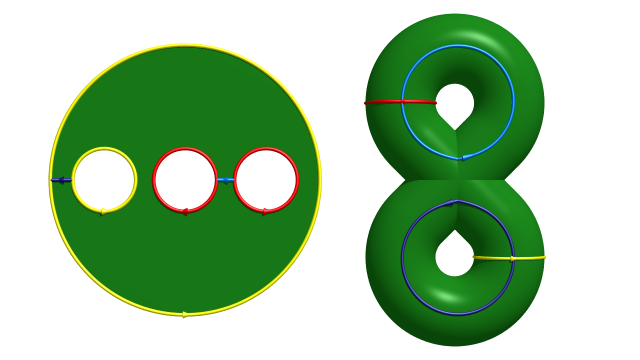
Mieux, en faisant passer les courbes $C_1, C_2,...,C_{2p}$ par un même point et en découpant la surface selon ces courbes, on obtient un polygone à $4p$ côtés conjugués $2$ à $2$, avec un seul cycle de sommets. Poincaré fait alors des rappels sur le groupe fondamental des surfaces [3], et détaille notamment le lien entre ses deux points de vues sur cet objet : comme groupe de classes d’homotopies de lacets, et comme groupe de transformations du revêtement universel.

Des polygones fuchsiens, pour quoi faire ?

Poincaré propose deux manières différentes de penser la surface $\Sigma_p$ de genre $p$. Dans les deux cas il est guidé par sa théorie des groupes fuchsiens [4]. Il n’est pourtant nullement question de géométrie ici mais seulement de topologie, c’est juste une manière commode (pour lui) de nous décrire deux manières de former une surface de genre $p$.

La première correspond à la situation où on découpe la surface $\Sigma_p$ le long des $p$ courbes fermées $C_1,C_3,\dots,C_{2p-1}$ évoquées ci-dessus. On voit alors $\Sigma_p$ comme une sphère privée de $2p$ disques dont on identifie par paires les $2p$ cercles composantes connexes du bord, comme dans la Zip-proof de Conway de la classification des surfaces. Poincaré qualifie la sphère privé de$2p$ disques de « polygone fuchsien de la 3ème catégorie ». Le groupe fuchsien correspondant est un groupe libre. Vu comme sous-groupe discret de $\mathrm{PSL} (2 , \mathbb{C})$, c’est ce qu’on appelle aujourd’hui un groupe de Schottky. Il opère par homographies sur un ouvert $\Omega$ de la sphère de Riemann $\mathbb{C} \cup \{ \infty \}$. Son domaine fondamental est une sphère privée de $2p$ disques, c’est le « polygone fuchsien de la 3ème catégorie » dont parle Poincaré. On notera que le revêtement $\Omega$ n’est pas simplement connexe (c’est la sphère de Riemann privé d’un ensemble de Cantor) et que le groupe fuchsien n’est pas isomorphe au groupe fondamental de $\Sigma_p$ ; c’est un quotient non-trivial de $\pi_1 (\Sigma_p )$.

L’animation suivante part du domaine fondamental et montre l’action des deux générateurs du groupe fuchsien, puis construit itérativement l’ouvert $\Omega$ pavé par l’ensemble des images du domaine fondamental par l’action du groupe.

Ce point de vue présente l’avantage pour la suite de singulariser $p$ courbes simples fermées disjointes sur la surface ; les courbes $C_1 , C_3 , \ldots , C_{2p-1}$ [5].

La deuxième manière de penser correspond à la situation où on découpe la surface $\Sigma_p$ le long des $2p$ courbes $C_1,C_2,\dots,C_{2p}$ (après les avoir déformées pour les faire passer par un même point). On voit alors $\Sigma_p$ comme espace d’identification d’un polygone à $4p$ côtés, dont on recolle les côtés par paires, comme dans l’animation plus haut. On peut réaliser ce polygone dans le plan hyperbolique $\mathbb{H}$ de sorte que les $4p$ côtés soient conjugués deux à deux par des isométries, qu’il n’y ait q’un seul cycle de sommets et que la somme des angles soit égale à $2\pi$. Le groupe fondamental de $\Sigma_p$ s’identifie alors au groupe fuchsien correspondant, et son revêtement universel à $\mathbb{H}$, ou au disque unité, pavé par des polygones congruents.

$$ $$

Caractérisation des automorphismes de $H_1(\Sigma_p,\mathbb{Z})$ qui sont induits par un difféomorphisme de la surface

Le résultat central de cette partie est :

La condition nécessaire et suffisante pour que la surface $S$ soit homéomorphe à elle-même de telle façon qu’aux cycles $C_i$ correspondent des cycles homologues aux cycles $C'_i$, c’est que la forme $F(x,y)$ relative aux cycles $C$ soit identique à la forme $F(x',y')$ relative aux cycles $C'$.

ce qui se traduit de façon moderne par :

Le fait que l’image de $i$ soit incluse dans $\mathrm{Aut}_F(H_1(\Sigma_p,\mathbb{Z}))$, c’est-à-dire que l’action d’un homéomorphisme en homologie préserve la forme d’intersection, est immédiat.

L’article consacré au groupe modulaire des surfaces donne la preuve de l’inclusion réciproque : on rappelle que l’action d’un twist de Dehn $T_a$ autour d’une courbe simple fermée qui représente l’élément $a \in H_1(\Sigma_p, \mathbb Z)$ est la transvection symplectique

$$b \mapsto b+F(a,b)a.$$

On démontre ensuite le lemme algébrique « classique » qui affirme que le groupe $\mathrm{Aut}_F(H_1(\Sigma_p,\mathbb{Z}))$ est bien engendré par les transvections symplectiques.

C’est plus ou moins la méthode qu’emploie Poincaré. Toutefois, au final, Poincaré a pour but de démontrer qu’un élément primitif dans $H_1(\Sigma_p, \mathbb Z)$ est représenté par une courbe simple fermée (voir le théorème ci-dessous). En admettant ce résultat il n’est pas difficile de montrer que toute transvection symplectique est l’image par $i$ d’un homéomorphisme de la surface $\Sigma_p$. Mais Poincaré ne peut se servir du résultat qu’il cherche à démontrer [6]. Il donne donc un (autre) système (fini) de générateurs explicites dont il montre par la suite qu’ils sont tous dans l’image de $i$.

Il est plus facile de travailler avec des matrices. Pour tout $i$ compris entre $1$ et $2p$, notons donc $e_i$ la classe du lacet $C_i$ dans $H_1(\Sigma_p, \mathbb Z)$. La base

$$(e_1 , e_3 , \ldots , e_{2p-1} , e_2 , e_4 , \ldots , e_{2p} )$$

permet d’identifier $H_1(\Sigma_p, \mathbb Z)$ à $\mathbb{Z}^{2p}$. Dans cette base, la matrice de $F$ est

$$J_{2p} = \left( \begin{array}{cc} 0 & I_p \\ -I_p & 0 \end{array} \right)$$

et le groupe $\mathrm{Aut}_F(H_1(\Sigma_p,\mathbb{Z}))$ s’identifie à $\mathrm{Sp}(2p,\mathbb{Z})$.

Étape 1. Générateurs de $\mathrm{Sp}(2p, \mathbb Z)$.

Pour le démontrer, voyons quelles sont les substitutions linéaires qui n’altèrent pas la forme $F$ que nous supposerons réduite.

Dans $\mathrm{Sp}(2p,\mathbb{Z})$ Poincaré considère plus précisément l’ensemble des matrices élémentaires symplectiques constitué d’une part des matrices du type

$$\tag{1} \left( \begin{array}{cc} I_p & \pm E_{k,k} \\ 0 & I_p \end{array} \right) \quad \left( 1 \leq k \leq p \right),$$

et de leurs transposées, et d’autre part des matrices

$$\tag{2} \left( \begin{array}{cc} I_p \pm E_{j,i} & 0 \\ 0 & I_p \mp E_{i,j} \end{array} \right) \quad \left( 1 \leq i \neq j \leq p \right).$$

Il affirme alors :

il est aisé de voir que toute substitution qui n’altère pas la forme réduite $F$ peut être considérée comme une combinaison de substitutions rentrant dans ces deux types.

Autrement dit,

La première démonstration publiée de ce résultat semble être due à Brahana [7] qui fait référence à Poincaré [8].

Démonstration de la proposition.

Vérifions maintenant que les matrices symplectiques élémentaires que Poincaré introduit suffisent bien à engendrer le groupe $\mathrm{Sp} (2p , \mathbb{Z})$. Un résultat plus classique, qui se déduit de l’algorithme d’Euclide sur $\mathbb{Z}$ et est généralement attribué à Witt [9], affirme que les matrices du type

$$\tag{3} \left( \begin{array}{cc} I_p & S \\ 0 & I_p \end{array} \right) \quad \left( S \in \mathcal{M}_p (\mathbb{Z} ) , \ {}^t S = S \right),$$

leurs transposées, les matrices du type

$$\tag{4} \left( \begin{array}{cc} {}^t U & 0 \\ 0 & U^{-1} \end{array} \right) \quad \left( U \in \mathrm{GL}_p (\mathbb{Z} ) \right),$$

et la matrice $J_{2p}$ engendrent le groupe $\mathrm{Sp} (2p , \mathbb{Z})$.

Il est classique que les matrices $I_p \pm E_{i,j}$ engendrent le groupe $\mathrm{GL}_p (\mathbb{Z})$ et donc que les matrices (2) engendrent le groupe de toutes les matrices (4). Par ailleurs les identités

$$\left( \begin{array}{cc} {}^t (I_p + E_{i,j}) & 0 \\ 0 & (I_p + E_{i,j})^{-1} \end{array} \right) \left( \begin{array}{cc} I_p & E_{i,i} \\ 0 & I_p \end{array} \right) \left( \begin{array}{cc} {}^t (I_p + E_{i,j})^{-1} & 0 \\ 0 & (I_p + E_{i,j}) \end{array} \right)$$

$$= \left( \begin{array}{cc} I_p & E_{i,i}+E_{j,i} + E_{i,j} + E_{j,j} \\ 0 & I_p \end{array} \right)$$

et

$$ \left( \begin{array}{cc} I_p & E_{i,i} + E_{j,j} \\ 0 & I_p \end{array} \right) \left( \begin{array}{cc} I_p & E_{i,i}+E_{j,i} + E_{j,j} + E_{i,j} \\ 0 & I_p \end{array} \right) \left( \begin{array}{cc} I_p & - E_{i,i} - E_{j,j} \\ 0 & I_p \end{array} \right) $$

$$= \left( \begin{array}{cc} I_p & E_{j,i} + E_{i,j} \\ 0 & I_p \end{array} \right)$$

impliquent que les matrices (3) appartiennent au groupe engendré par les matrices (1) et (2). Finalement, l’identité

$$ \left( \begin{array}{cc} 0 & I_p \\ -I_p & 0 \end{array} \right) = \left( \begin{array}{cc} I_p & I_p \\ 0 & I_p \end{array} \right) \left( \begin{array}{cc} I_p & 0 \\ - I_p & I_p \end{array} \right) \left( \begin{array}{cc} I_p & I_p \\ 0 & I_p \end{array} \right)$$

implique que la matrice $J_{2p}$ appartient elle aussi au groupe engendré par les matrices (1) et (2). Comme annoncé par Poincaré, les matrices symplectiques élémentaires engendrent donc tout le groupe symplectique.

$$ $$

Étape 2. Il s’agit maintenant de vérifier que chacune des ces matrices correspond à l’action en homologie d’un homéomorphisme de la surface.

Celles du premier type (que Poincaré traite en deuxième) correspondent aux twists de Dehn le long des cycles fondamentaux. L’animation suivante représente un twist de Dehn sur le tore.

Et celle-ci sur une surface de genre 3

Dans le cas étudié par Poincaré, l’image par $i$ du twist de Dehn le long de $C_2$ envoie $e_1$ sur $e_1+e_2$ et laisse les autres générateurs invariants, donc la matrice correspondante est $\left( \begin{smallmatrix} I_p & E_{1,1} \\ 0 & I_p \end{smallmatrix} \right)$. De manière analogue Poincaré vérifie ainsi que toutes les matrices élémentaires symplectiques du premier type sont images par $i$ d’un twist de Dehn le long d’un cycle fondamental.

L’argument de Poincaré.

Poincaré adopte un mode de représentation intermédiaire entre les deux points de vue du début. Il voit $\Sigma_p$ comme un carré privé de $2p-2$ disques disjoints. Les côtes opposés du carré sont identifiés pour former un tore privé de $2p-2$ disques identifiés deux à deux pour attacher $p-1$ anses au tore. Poincaré considère le revêtement de $\Sigma_p$ de groupe $\mathbb{Z}^2$ obtenu en pavant le plan par des carrés avec $p$ anses attachées, comme dans l’animation suivante.

L’action de la matrice $\left( \begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix} \right)$ représentée dans l’animation suivante induit un twist de Dehn sur le tore. Dans notre cas, si les $p-1$ anses attachées au carré sont supposées toutes contenues dans l’un des deux triangles, il correspond à la matrice $\left( \begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix} \right)$ un difféomorphisme de la surface $\Sigma_p$ qui est bien un twist de Dehn comme expliqué ci-dessus.

$$ $$

Montrons maintenant que les matrices élémentaires symplectiques du deuxième type sont elles aussi images par $i$ d’un homéomorphisme (ici dans le texte original). Si pour le « premier type » on pensait tout naturellement à un twist de Dehn, il est moins évident ici d’imaginer directement un homéomorphisme de la surface ayant l’action voulue en homologie. Suivons donc Poincaré qui, comme dans le cas précédent, travaille sur un revêtement de la surface, et nous visualiserons ensuite seulement l’homéomorphisme de la surface elle-même, à l’aide d’une animation.

De la même manière que dans le cas des transformations du premier type on se ramenait au cas du tore, on peut se ramener ici à une surface de genre $2$. En effet, si $p\ge 2$, il suffit de penser $\Sigma_p$ comme $\Sigma_2$ avec $p-2$ anses attachées (à un disque $D\subset \Sigma_2$), et de construire l’homéomorphisme recherché à support dans $\Sigma_2$ privé de $D$.

Comme pour les twists de Dehn, donc, Poincaré construit l’homéomorphisme recherché sur un revêtement de la surface. Il pense en effet celle-ci comme un polygone fuchsien de la troisième famille, autrement dit comme le quotient d’un ouvert $\Omega$ de la sphère par un groupe libre de rang $2$, dont les générateurs correspondent aux lacets $C_2$ et $C_4$. L’animation suivante montre le « polygone » en question et ses images par l’action du groupe libre, qui pavent l’ouvert $\Omega$ (la sphère privée d’un Cantor).

La figure suivante représente un domaine fondamental pour l’action du groupe libre sur $\Omega$ : la sphère de Riemann privé de quatre disques bordés par les courbes $A_1,A_1',A_3,A_3'$ obtenues par découpage de la surface $\Sigma_2$ le long des courbes $C_1$ et $C_3$. C’est le fameux polygone fuchsien de la troisième famille de Poincaré.

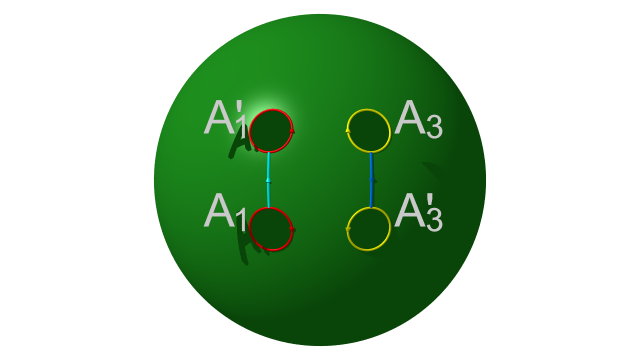
Les deux générateurs du groupe libre correspondant à $C_2$ et $C_4$ identifient respectivement $A_1$ à $A_1'$ et $A_3$ à $A_3'$. Au quotient on obtient les courbes simples fermées $C_1$ et $C_3$.

Poincaré considère alors une courbe fermée simple $B$ qui enveloppe les deux courbes $A_1$ et $A_3$, comme représenté ci-dessous.

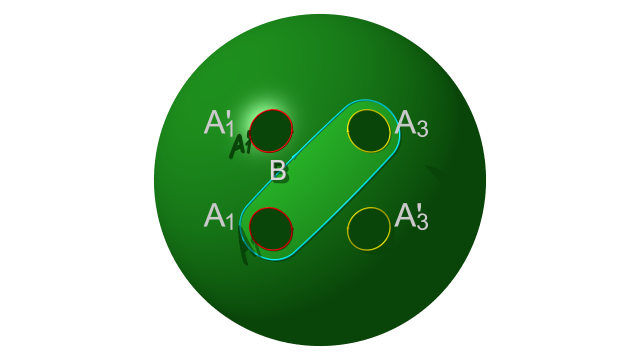
La courbe $B$ se projette dans la surface en une courbe simple fermée homologue à $C_1+C_3$. Dans un premier temps, d’ici à là, Poincaré construit un homéomorphisme de $\Omega$ qui commute à l’action du groupe libre et envoie $A_1$ sur $B$. Pour ce faire, il considère le disque à deux trous $\Delta$ bordé par les courbes $B$, $C_1$ et $C_3$. Poincaré considère le domaine $\Omega'$ obtenu à partir de $\Omega$, en remplaçant $\Delta$, par son image par l’automorphisme de revêtement associé à $C_2$. Par construction, il s’agit d’un nouveau domaine fondamental pour l’action du groupe libre engendré par les automorphismes associés à $C_2$ et $C_4$. Par ailleurs, ce nouveau domaine fondamental $\Omega'$ est, tout comme $\Omega$, une sphère à privée de quatre disques [10]. Ainsi, $\Omega'$ est homéomorphe à $\Omega$, via un homéomorphisme qui envoie $A_1$ sur $B$, préserve $A_3$ et passe au quotient. L’action du groupe libre permet d’étendre cet homéomorphisme en un homéomorphisme de $\Omega$ dans lui-même (qui commute donc à l’action du groupe libre). La construction de $\Omega'$, et l’homéomorphisme entre $\Omega'$ et $\Omega$ sont representés dans l’animation suivante.

Au quotient, l’homéomorphisme entre $\Omega$ et $\Omega'$ induit un homéomorphisme de la surface $\Sigma_2$ qui envoie la courbe $C_1$ sur l’image de la courbe $B$ dans la surface, homologue à $C_1+C_3$ par construction, et préserve la courbe $C_3$, donc qui agit comme souhaité sur deux des vecteurs de base de l’homologie. Reste à vérifier que cet homéomorphisme a l’action voulue sur les deux autres vecteurs de base. L’argument de Poincaré est difficile à suivre sans images [11]. Nous le remplaçons par les animations suivantes, on l’on visualise cette transformation de la surface vue non pas comme quotient mais comme plongée dans $\mathbb{R}^3$ de façon standard. On peut en fait réaliser l’homéomorphisme par une isotopie de l’espace ambiant [12]. On commence par décrire la transformation inverse : partant de la courbe $B$, on décrit une isotopie de l’espace ambiant qui envoie la surface sur elle-même et la courbe $B$ sur la courbe $C_1$.

On visualise maintenant l’isotopie inverse, qui envoie donc $C_1$ sur $B$, après avoir pris soin d’ajouter les courbes $C_2$ (bleu clair), $C_3$ (jaune) et $C_4$ (bleu foncé), et on vérifie, comme Poincaré, que l’homéomorphisme obtenu opère en homologie comme la matrice élémentaire symplectique recherchée : les courbes $C_1$, $C_2$, $C_3$ et $C_4$ sont envoyées sur respectivement

$$C_1 ' = C_1+C_3 , \ C_2 ' = C_2, \ C_3 ' = C_3 \mbox{ et } \ C_4 ' = C_4 -C_2.$$

On peut remarquer que la matrice élémentaire symplectique obtenue est aussi l’image du produit suivant de twists de Dehn :

$$T_{C_3}^{-1} T_{C_2} T_{C_3 + C_2},$$

où l’on a abusivement noté $C_3+C_2$ la classe d’homotopie de l’unique courbe simple fermée homologue à $C_3+C_2$.

Combinaisons des cycles fondamentaux homologues à des courbes fermées simples

Poincaré déduit de l’énoncé précédent la caractérisation suivante des cycles « non bouclés » :

un cycle $\sum a_iC_i$ est toujours homologue à un cycle non-bouclé, c’est-à-dire ne se coupant pas lui-même, si les entiers $a_i$ sont premiers entre eux. Si, au contraire, ces entiers $a_i$ ne sont pas premiers entres eux, il ne peut être homologue à un cycle non bouclé.

En termes modernes :

Démonstration. (D’ici jusqu’à la fin dans le texte original.) Poincaré commence par montrer que la condition est suffisante. D’après le théorème précédent, il suffit de montrer qu’un tel élément peut être complété en une base symplectique du $H_1$, car alors il existera un homéomorphisme de $S$ dont l’action induite en homologie enverra $C_1$ sur $C'_1$, ce qui voudra dire que $C'_1$ est la classe d’homologie de l’image d’un lacet simple par un homéomorphisme, qui est encore un lacet simple (voir ici dans le texte original).

Il s’agit donc en d’autres termes de montrer que $\mathrm{Sp}(2p,\mathbb{Z})$ opère transitivement sur les éléments primitifs de $\mathbb{Z}^{2p}$. Cela résulte de l’algorithme d’Euclide comme il est expliqué dans l’article consacré au groupe modulaire des surfaces.

La démonstration de Poincaré.

Poincaré commence par remarquer que le groupe $\mathrm{SL}_{2p} (\mathbb{Z} )$ opère transitivement sur les éléments primitifs de $\mathbb{Z}^{2p}$ :

Remarquons d’abord que si les entiers $a_i$ sont premiers entre eux, on pourra trouver $2p$ cycles

$$C''_1, C''_2, \ldots, C''_{2p}$$

tels que

$$C''_1 = C'_1 = \sum a_i C_i,\quad C''_k = \sum b_{ik} C_i,$$

les $a_i$ et les $b_{ik}$ étant des entiers dont le déterminant soit égal à $1$.

Autrement dit, si $v \in \mathbb{Z}^{2p}$ est primitif, il existe un élément $g \in \mathrm{SL}_{2p} (\mathbb{Z} )$ tel que $g(e_1) = v$. Il s’agit de montrer que l’on peut prendre $g$ dans $\mathrm{Sp} (2p , \mathbb{Z} )$. À ce stade, la transformation $g$ ne préserve a priori pas la forme $F$ mais la transforme en une forme symplectique ${}^t g F g$ de matrice

$$\left( \begin{array}{cc} 0 & u \\ -{}^t u & \Phi \end{array} \right).$$

Les coefficients de $u$ sont premiers ensembles puisque ${}^t g F g$ est de déterminant $1$. Le groupe $\mathrm{SL}_{2p-1} (\mathbb{Z} )$ opérant transitivement sur les vecteurs primitifs de $\mathbb{Z}^{2p-1}$. Il existe une matrice $A \in \mathrm{SL}_{2p-1} (\mathbb{Z} )$ telle que

$$ \left( \begin{array}{cc} 1 & 0 \\ 0 & {}^t A \end{array} \right) \left( \begin{array}{cc} 0 & u \\ -{}^t u & \Phi \end{array} \right) \left( \begin{array}{cc} 1 & 0 \\ 0 & A \end{array} \right)$$

$$= \left( \begin{array}{ccc} 0 & 1 & 0 \\ 1 & 0 & w \\ 0 & -{}^t w & \psi \end{array} \right)$$

où $w$ est un vecteur primitif de $\mathbb{Z}^{2p-2}$ et $\psi$ est une matrice antisymétrique de taille $2p-2$. Finalement, en se servant du coefficient $1$ comme d’un pivot on conclut qu’il existe une transformation $g \in \mathrm{SL}_{2p} (\mathbb{Z} )$ telle que $g(e_1)=v$ et ${}^t g F g$ soit de la forme

$$\left( \begin{array}{ccc} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & \psi \end{array} \right)$$

et par récurrence on conclut que l’on peut supposer que $g$ préserve $F$.

$$ $$

Il reste à montrer la réciproque, c’est-à-dire que si un élément $\sum a_i C_i\in H_1(\Sigma_p,\mathbb{Z})\simeq \mathbb{Z}^{2p}$ admet pour représentant un lacet simple, alors les $a_i$ sont premiers entre eux. Poincaré y consacre le reste du paragraphe 3. Sa démonstration est un peu compliquée à suivre. Il suffit en fait de remarquer que si $\alpha$ et $\beta$ sont deux lacets simples fermés non séparants sur $\Sigma = \Sigma_p$ alors il existe un homéomorphisme $\phi$ de $\Sigma$ préservant l’orientation qui envoie $\alpha$ sur $\beta$.

Besoin d’une démonstration ?

Les surfaces à bord $\Sigma_\alpha$ et $\Sigma_\beta$ obtenues en découpant $\Sigma$ respectivement selon $\alpha$ et selon $\beta$ sont compactes connexes de même caractéristique d’Euler et avec le même nombre de composantes de bord. Elles sont donc homéomorphes. Finalement un homéomorphisme entre $\Sigma_\alpha$ et $\Sigma_\beta$ induit un homéomorphisme de $\Sigma$ qui envoie $\alpha$ sur $\beta$.

$$ $$

Il existe en particulier une transformation $g \in \mathrm{Sp} (2p , \mathbb{Z} )$ qui envoie $C_1$ sur $\sum a_i C_i\in H_1(\Sigma_p,\mathbb{Z})\simeq \mathbb{Z}^{2p}$ et les $a_i$ sont premiers entre eux.