|
> Homologie > Homologies polyédrale et simpliciale > Invariance par subdivision Invariance par subdivision |
Par définition, les polyèdres viennent équipées d’une classe de cellulations (linéaires) compatibles privilégiées. Chacune de ces cellulations est un complexe (linéaire) auquel on a associé ici des groupes d’homologie. L’objet de cet article est de montrer que ces groupes ne dépendent en fait que du polyèdre et pas du choix particulier de cellulation.
Subdivision et morphisme associé
Soit $X$ un polyèdre et soit $K$ une cellulation de $X$, de sorte que $|K| =X$.
On dit qu’une cellulation $K'$ de $X$ est une subdivision de $K$, et on écrit $K^{\prime} < K$, si pour toute cellule $\sigma' \in K'$, il existe une cellule $\sigma \in K$ telle que $|\sigma '| \subset |\sigma |$.
En intersectant deux cellulations on peut montrer que les cellulations d’un polyèdre sont compatibles c’est-à-dire que si $K_1$ et $K_2$ sont deux cellulations d’un polyèdre $X$, elles admettent une subdivision commune $K_0$ :
$$K_0 < K_1 \quad \mbox{ et } \quad K_0 < K_2 .$$
Supposons maintenant fixée une subdivision $K^{\prime} < K$. Il lui correspond la famille des applications linéaires $F_i$ de $C_i = C_i (K)$ vers $C_i ' = C_i (K')$ qui associent à toute cellule $\sigma \in K^{(i)}$ la somme
$$F_i (\sigma) = \sum_{\substack{\sigma ' \in K' {}^{(i)} \\ |\sigma' | \subset |\sigma |}} \pm \sigma',$$
où le signe $\pm$ est $+$ si les orientations de $\sigma$ et $\sigma '$ sont compatibles et $-$ sinon.
La proposition suivante est immédiate mais fondamentale.
L’application $F =(F_i) : C_{\bullet} \to C_{\bullet} '$ est un morphisme de complexes, autrement dit $F= (F_i)$ est une suite d’applications linéaires telles que le diagramme
$$ \begin{CD} \cdots @>>> C_i @> \partial >> C_{i-1} @> \partial >> C_{i-2} @>>> \cdots \\ @. @V F_i VV @V F_{i-1} VV @V F_{i-2} VV \\ \cdots @>>> C_i^{\prime} @> \partial >> C_{i-1}^{\prime} @> \partial >> C_{i-2}^{\prime} @>>> \cdots \end{CD} $$
soit commutatif.
Théorème d’invariance par subdivision
Noter que si $\alpha \in C_i$ est un cycle, il découle de la proposition que $F (\alpha)$ est également un cycle :
$$\partial F (\alpha) = F (\partial \alpha ) = 0.$$
De la même manière $F$ envoie $B_{\bullet}$ dans $B_{\bullet} '$. Un morphisme de complexe induit donc un morphisme entre les groupes d’homologie de ces complexes.
Le morphisme de complexes $F: C_{\bullet} (K) \to C_{\bullet} (K')$ est un quasi-isomorphisme, c’est-à-dire qu’il induit un isomorphisme au niveau des groupes d’homologie.
Démonstration. [1] On montre ici que les cellulations $K$ et $K'$ du polyèdre $X$ possèdent une subdivision commune $K_0$ qui est une subdivision par bisections de $K$ et de $K'$. Le théorème découle donc du lemme suivant.
C.Q.F.D.
$$ $$
Soit $K'$ une subdivision de $K$ résultant d’une bisection élémentaire. Alors le morphisme de complexes $F: C_{\bullet} (K) \to C_{\bullet} (K')$ est un quasi-isomorphisme.
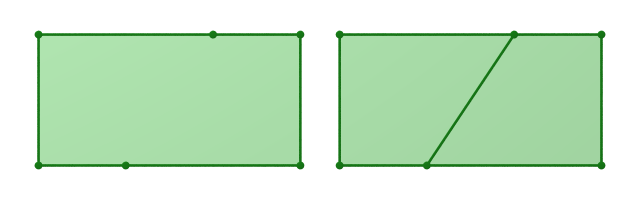
Démonstration. Soit $\sigma$ la cellule de $K$ telle que $K'$ est obtenue à partir de $K$ en remplaçant $\sigma$ par trois cellules $\sigma_-$, $\sigma_+$ et $\sigma_0$ comme sur la figure ci-dessous.
La cellule $\sigma_0$ est obtenue en formant l’intersection de $\sigma$ avec un hyperplan de l’espace euclidien ambiant et cet hyperplan découpe $\sigma$ en deux cellules non-vides $\sigma_+$ et $\sigma_-$. Soit $n$ la dimension de $\sigma_0$, égale à la dimension de $\sigma$ moins $1$. Pour tout $i$, on a :
$$C_{i} (K') = C_{i} ' \oplus C_{i} (K),$$
où $C_{n+1} ' = \mathbb{Z} [ \sigma_+ ]$, $C_n ' = \mathbb{Z} [\sigma_0 ]$ et est égal à $\{0 \}$ en tous les autres degrés. On en déduit que
$$Z_{n+1} (K' ) = Z_{n+1} (K) \quad \mbox{ et } \quad B_{n+1} (K' ) = B_{n+1} (K)$$
et
$$Z_{n} (K' ) = Z_{n} (K) \oplus \mathbb{Z} [\partial \sigma_+] \quad \mbox{ et } \quad B_{n} (K' ) = B_{n} (K) \oplus \mathbb{Z} [\partial \sigma_+ ].$$
Le lemme s’en déduit.
C.Q.F.D.
$$ $$
Homologie des polyèdres
Il résulte du théorème, et du fait que les cellulations d’un polyèdre sont compatibles, que l’on dispose d’une théorie homologique des polyèdres qui est naturelle relativement aux applications PL
Soit $X$ un polyèdre. On appelle homologie polyédrale $H_\bullet (X)$ de $X$ l’homologie $H_\bullet (K)$ où $K$ est une cellulation quelconque de $X$.
Homologie des variétés ?
Toute variété lisse admet une cellulation lisse, unique à homéomorphisme PL près, ce qui la munit en particulier d’une structure de variété PL. C’est le contenu du théorème de Whitehead. Il s’en suit que l’on peut définir les groupes d’homologie d’une variété lisse comme étant ceux de son polyèdre associé et que les groupes d’homologies de deux variétés lisses difféomorphes sont isomorphes. À ce stade, il n’est toutefois pas évident que l’on obtient ainsi une théorie homologique naturelle : si $f:X \to Y$ est une application continue entre polyèdres, ou même une application lisse entre variétés lisses, il n’est pas immédiat que $f$ induise une application linéaire $f_*$ au niveau des groupes d’homologie. Pour démontrer cela on peut soit avoir recours à l’approximation simpliciale soit, comme on le propose ici en suivant Poincaré, identifier l’homologie polyédrale à une théorie homologique plus abstraite, comme l’homologie singulière.
[1] Poincaré propose une démonstration légèrement différente de ce théorème dans les paragraphes IV et V du Premier Complément à l’Analysis Situs. Nous commentons (et complétons) cette démonstration ici.