|
> Groupe fondamental > Groupe fondamental par les lacets > Revêtement universel Revêtement universel |
On a vu que l’écriture d’un espace $X$ sous la forme $\Gamma\backslash Y$ fournit une description de $X$ particulièrement intéressante. Nous allons voir que tous les espaces raisonnables (en particulier les variétés et les CW-complexes) s’écrivent de cette façon.
Toute variété ou CW complexe peut s’écrire comme quotient d’un espace $1$-connexe $Y$ par un groupe $\Gamma$ agissant topologiquement librement.
On sait déjà que $\Gamma$ s’identifie au groupe fondamental de $X$. Il nous reste donc à construire $Y$. Cet espace sera le revêtement universel de $X$. C’est le « plus grand » revêtement connexe d’un espace topologique.
Nous dirons qu’un revêtement $p:Y \to X$ est dit universel si $Y$ est $1$-connexe [1].
Par définition, si $X=\Gamma\backslash Y$ où $Y$ est $1$-connexe et $\Gamma$ agit de façon topologiquement libre alors $p : Y\to X$ est un revêtement universel. Une version plus faible du théorème précédent est donc la suivante.
Si $X$ est une variété ou un CW-complexe connexe, alors $X$ admet un revêtement universel.
On verra dans la classification des revêtements que le revêtement universel $\widetilde{X}$, est essentiellement unique. En particulier, si $Y \to X$ est un revêtement (avec $Y$ connexe) et que $ \widetilde{Y} \to Y$ est le revêtement universel de $Y$, la composée $ \widetilde{Y} \to Y \to X$ est « le » revêtement universel de $X$. Cela justifie l’appellation : le revêtement est universel parce qu’il est « au-dessus » de tous les revêtements (connexes).
Description du revêtement universel à l’aide de lacets
Commençons par voir à quoi pourrait ressembler un revêtement universel.
Si $(Y,y_0) \to (X,x_0)$ est un revêtement universel, la simple connexité de $Y$ signifie que les classes d’homotopie (à extrémités fixées) de chemins $I \to Y$ issus de $y_0$ sont naturellement en bijection avec les points de $Y$ via l’application $[\tilde\sigma]\mapsto \tilde\sigma(1)$. Mais le relèvement des chemins met en bijection les classes d’homotopie (à extrémités fixées) de chemins $ \sigma : I \to X$ issus de $x_0$ et la classe d’homotopie (à extrémités fixées) de leur unique relevé $\tilde\sigma : I \to X$ issu de $y_0$. Ainsi, si le revêtement universel existe, son espace total s’identifie à l’espace
$$ P(X, x_0) = \{ \mbox{lacets }\sigma : I \to X \mbox{ tels que } \sigma(0) = x_0\} \Big / \mbox{homotopie à extrémités fixées}$$
et l’application de revêtement $p : P(X, x_0) \to X$ associe simplement à la classe du chemin $\sigma : I \to X$ son extrémité $\sigma(1) \in X$. C’est exactement le principe de la construction de $\widetilde{X}$ !
En outre, la concaténation des chemins fournit une action (à gauche)
$$ \begin{array}{cccc} &\pi_1(X, x_0) \times P(X, x_0)&\longrightarrow &P(X, x_0)\\ &([\gamma], [\sigma])&\longmapsto& [\gamma*\sigma]. \end{array} $$
Il existe une topologie sur $P(X, x_0)$, pour laquelle $p : P(X, x_0)\to X$ est un revêtement universel de $X$.
Preuve de l’existence du revêtement universel
Nous allons démontrer la proposition ci-dessus (dont découle immédiatement le théorème d’existence d’un revêtement universel). Notons que les hypothèses sur $X$ nous assurent que chaque point $x$ de $X$ admet un voisinage $U$ qui se rétracte sur $X$. On dit alors que $U$ est contractile.
Commençons par définir une topologie sur $P(X, x_0)$, pour cela on se donne une base de la topologie : soit $[\sigma]\in P(X, x_0)$ et $U$ un voisinage contractile de $\sigma(1)$, on pose
$$U_{[\sigma]}=\{[\sigma * \tau]\in P(X, x_0) \text{ où } \tau\in\Omega(U,x) \}.$$
On note $\mathcal U$ l’ensemble des $U_{[\sigma]}$ et $\mathcal T$ la topologie engendrée par les éléments de $\mathcal U$. Par construction, les éléments de $\mathcal U$ forment une base de la topologie $\mathcal T$.
L’application
$$ \begin{array}{cccc} p: &P(X, x_0)&\longrightarrow &X\\ &[\sigma]&\longmapsto& \sigma(1) \end{array} $$
est un revêtement.
Démonstration. Remarquons que les ouverts contractiles forment une base de la topologie de $X$. Soient $x\in X$ et $U$ un voisinage contractile de $x$. Soit $[\sigma]\in P(X, x_0)$ tel que $\sigma(1)=x$. Alors $p(U_{[\sigma]})\subset U$ et $p$ est continue.
Montrons maintenant que
$$p^{-1}(U)=\coprod_{[\sigma]\in p^{-1}(x)} U_{[\sigma]}.$$
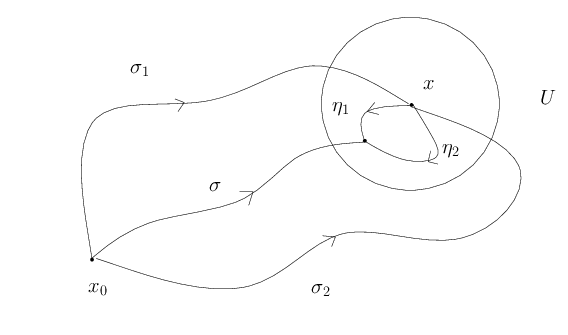
Soit $\gamma \in p^{-1}(U)$, alors $\gamma(1)\in U$. Soit $\eta$ un chemin de $U$ reliant $\gamma(1)$ à $x$ (un tel chemin existe car $U$ est connexe par arcs). Alors $[\gamma]=[\gamma*\eta*\overline{\eta}]$ et $[\gamma*\eta]\in p^{-1}(x)$ donc $[\gamma]\in U_{[\gamma*\eta]}$.
Par définition de $U_{[\sigma]}$, on a $p(U_{[\sigma]})=U$ donc
$$p^{-1}(U)=\bigcup_{[\sigma]\in p^{-1}(x)} U_{[\sigma]}.$$
Cette union est disjointe car si $[\sigma]\in U_{[\sigma_1]}\cap U_{[\sigma_2]}$ alors $[\sigma]=[\sigma_1*\eta_1]=[\sigma_2*\eta_2]$. Or, $\sigma_1*\eta_1*\overline{\eta_2}*\overline{\sigma_2}$ est homotope à $\sigma*\overline{\sigma}$ donc contractile et $\eta_1*[\overline{\eta_2}]$ est contractile car $U$ est contractile. Par conséquent, $[\sigma_1]=[\sigma_2]$ et l’union est disjointe.
Soit $[\sigma]\in p^{-1}\{x\}$. Il reste à montrer que $p : U_{[\sigma]}\to U$ est un homéomorphisme. Pour ce faire, nous allons construire son inverse. Considérons l’application
$$ \begin{array}{cccc} q: & U &\longrightarrow& U_{[\sigma]}\\ &x'&\longmapsto& [\sigma*\eta] \end{array} $$
où $\eta$ est un chemin du $U$ reliant $x$ à $x'$. Comme $U$ est contractile, $q$ est bien définie. De plus $p\circ q= \mathrm{Id}_U$ et $q\circ p= \mathrm{Id}_{U_{[\sigma]}}$. Enfin $q$ est continue : soit $x'\in U$ et $V_{q(x')}$ un voisinage contractile de $q(x')$ tel que $V\subset U$, par définition de $q$, il vient $q(V)\subset V_{q(x')}$.
Ainsi, l’application continue $p : U_{[\sigma]}\to U$ admet un inverse continu $q: U \to U_{[\sigma]}$. Par conséquent, $p : U_{[\sigma]}\to U$ est un homéomorphisme, et le lemme est démontré.
C.Q.F.D.
L’espace $P(X, x_0)$ muni de la topologie $\mathcal T$ est connexe par arcs et $1$-connexe.
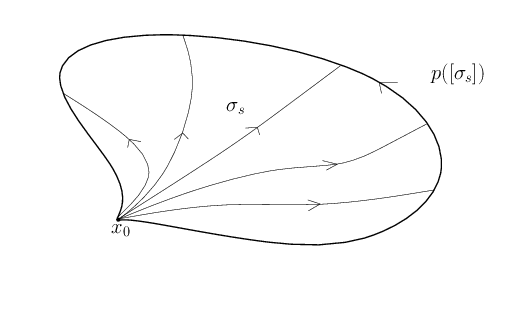
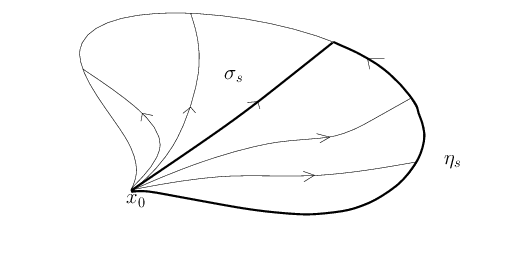
Démonstration. Soit $[\sigma]\in P(X, x_0)$. Alors $s\mapsto\sigma_s$ où $\sigma_s(t)=\sigma(st)$ est un chemin continu reliant $[c_{x_0}]$ à $[\sigma]$. Donc $P(X, x_0)$ est connexe par arcs.
Par le théorème de relèvement des homotopies pour montrer que $P(X, x_0)$ est $1$-connexe, il suffit de montrer que $p_*$ est nulle. Soit $s\to[\sigma_s]$ un lacet de $P(X, x_0)$ basé en $[c_{x_0}]$. On veut montrer que $s\to p[\sigma_s]$ est contractile.
Pour $s, t\in I$, on pose $\eta_s(t)=p([\sigma_{st}])$. Ainsi, pour tout $s \in I$, $[\eta_s]$ est un élément de $P(X, x_0)$. De plus, pour tout $s\in I$, on a $p([\sigma_s])=\sigma_s(1)=p([\eta_s])$. Par unicité du relèvement des chemin, on obtient donc $[\sigma_s]=[\eta_s]$ pour tout $s\in I$.
En particulier $[\eta_1]=[c_{x_0}]$ donc $p([\sigma_s])=\eta_1$ est contractile, et le lemme est démontré.
C.Q.F.D.
En mettant bout à bout les deux lemmes ci-dessus, on obtient une preuve de la proposition, et a fortiori une preuve du théorème d’existence d’un revêtement universel.
Étude de l’action du groupe fondamental sur la fibre
Nous étudions maintenant l’action du groupe fondamental $\pi_1(X,x_0)$ sur la fibre du revêtement universel $p:P(X, x_0)\to X$. La proposition ci-dessus résume les propriétés générales de cette action.
L’action $\pi_1(X, x_0)$ sur $P(X, x_0)$ est une action par homéomorphismes. Elle est topologiquement libre. Deux éléments $ x_1, x_2 \in X$ sont dans la même orbite si et seulement si $p( x_1) = p( x_2)$.
Démonstration. Soient $[\sigma]\in P(X, x_0)$ et $U$ un voisinage contractile de $\sigma(1)$. Soit $[\gamma]\in\pi_1(X, x_0)$. Alors $U_{[\gamma*\sigma]}= [\gamma]*U_{[\sigma]}$. Donc le groupe fondamental agit par homéomorphisme sur $P(X, x_0)$.
De plus $[\sigma']\in U_{[\sigma]}\cap U_{[\gamma*\sigma]}$ si et seulement si $[\sigma]=[\gamma*\sigma]$ et donc si et seulement si $[\gamma]=1$. Par conséquent l’action est topologiquement libre.
Enfin soient $[\sigma_1]$ et $[\sigma_2]$ dans $P(X, x_0)$. Si $[\sigma_1]$ et $[\sigma_2]$ sont dans la même orbite de l’action de $\pi_1(X,x_0)$, alors il existe $[\gamma]\in\pi_1(X, x_0)$ tel que $[\sigma_2]=[\gamma]*[\sigma_1]$ donc $p([\sigma_1])=p([\sigma_2])$. Réciproquement, si $p([\sigma_1])=p([\sigma_2])$ alors $[\sigma_1*\overline{\sigma_2}]\in \pi_1(X, x_0)$ et $[\sigma_1]=[\sigma_1*\overline{\sigma_2}]*[\sigma_2]$ donc $[\sigma_1]$ est dans l’orbite de $[\sigma_2]$.
C.Q.F.D.
Conditions d’existence du revêtement universel
Si l’espace considéré est une variété ou un CW-complexe, le revêtement universel existe toujours. Cependant, si on considère des espaces topologiques plus généraux, ce n’est pas toujours le cas. En plus de la condition de locale connexité par arcs que nous imposons par convention à tous nos espaces topologiques pour définir le groupe fondamental, la simple connexité de $\widetilde{X}$ a deux conséquences sur la topologie de $X$ :
- Tout d’abord, $p$ est surjective et $\widetilde{X}$ est connexe par arcs. Cela entraîne que $X$ doit être connexe par arcs.
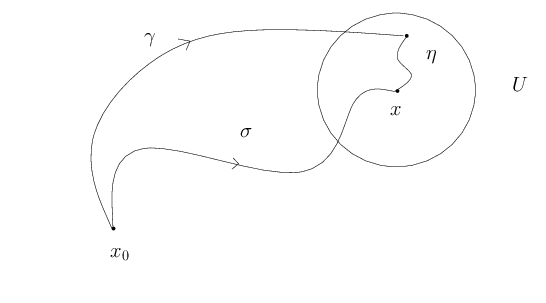
- Ensuite, si $\gamma$ est un lacet tracé sur $X$ suffisamment petit, celui-ci est inclus dans un ouvert trivialisant du revêtement. On peut en particulier le relever en un lacet $\gamma$ sur $X$. La simple connexité de $X$ implique alors que $\gamma$ est homotope à zéro, ce qui entraîne que $\gamma$ était homotope à zéro dans $X$.
Cette seconde propriété nous incite à poser la définition suivante.
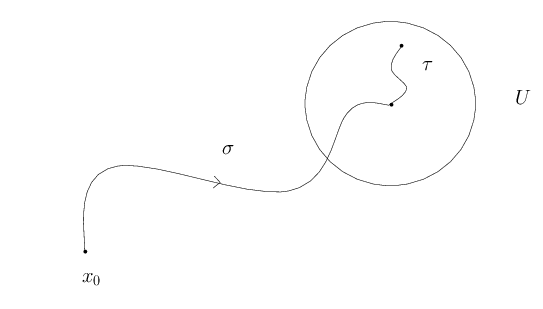
Un espace $X$ est délaçable si tout point $x$ admet un voisinage $U$ tel que le morphisme $\pi_1(U, x) \to \pi_1(X, x)$ induit par l’inclusion $U \hookrightarrow X$ soit nul.
On a alors l’existence d’un revêtement universel sous les deux conditions que l’on a dégagées. Il suffit d’adapter la preuve en remplaçant les ouverts contractiles par des ouverts connexes par arcs décrits dans la définition de délaçable.
Soit $X$ un espace topologique localement connexe par arcs. Alors $X$ admet un revêtement universel si et seulement si $X$ est connexe et délaçable.
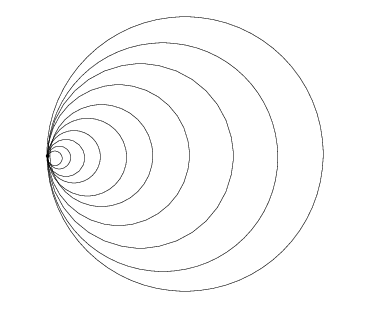
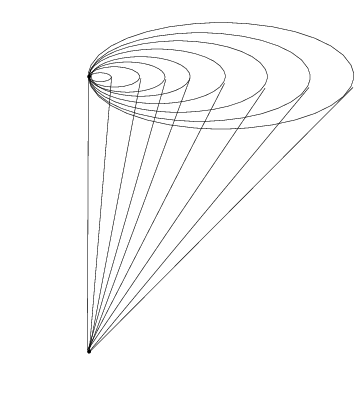
Un espace est délaçable si tout « petit » lacet est homotope à un lacet constant. L’homotopie n’est pas forcément petite comme le montre l’exemple suivant obtenu à partir de boucles d’oreilles hawaïennes.
Nous avons maintenant tous les éléments nécessaires pour décrire la classification des revêtements
[1] La définition de « revêtement universel » que nous donnons ici est naturelle dans notre approche du groupe fondamental « par les lacets ». Dans l’approche du groupe fondamental « par les revêtement », nous donnons une autre définition. Les deux notions coïncident... mais nous ne l’avons pas encore démontré ! Dans tout cet article, « revêtement universel » signifie donc « revêtement 1-connexe », et rien d’autre !