
|
> Groupe fondamental > Groupe fondamental par les lacets > Classification des revêtements et revêtements galoisiens Classification des revêtements et revêtements galoisiens |
Nous allons voir maintenant comment classer les revêtements à isomorphisme près. L’objet clé de cette classification est le groupe $H(p, x_0, y_0) = p_*( \pi_1(Y, y_0))\subset \pi_1(X, x_0)$ associé à un revêtement pointé $p :(Y,y_0)\to (X,x_0)$. On rappelle que $p_*(\pi_1(Y,y_0))$ est le stabilisateur de $y_0$ sous l’action de $\pi_1(X,x_0)$. La classification s’exprime mieux dans le cas des revêtements pointés.
L’application
$$\begin{array}{ccc} \{ \textrm{revêtements pointés connexes de }X\}&\longrightarrow &\{\textrm{sous-groupes de } \pi_1(X, x_0)\}\\ p : (Y, y_0) \to (X, x_0)&\longmapsto&H(p, x_0, y_0) \end{array}$$
est une bijection.
Démonstration. Commençons par montrer que cette application est injective : soit $p : (Y,y_0)\to (X,x_0)$ et $p' : (Y',y'_0)\to (X,x_0)$ deux revêtements tels que $H(p, x_0, y_0)=H(p', x_0, y'_0)$.
$$\xymatrix{ & (Y',y'_0)\ar[d]^{p'} \\ (Y,y_0) \ar[r]^p & (X,x_0).}$$
Par le théorème de relèvement des applications, il existe un relevé $\widetilde{p} : (Y,y_0)\to (Y',y'_0)$ de $p$ et un relevé $\widetilde{p}' : (Y',y'_0)\to (Y,y_0)$ de $p'$.
$$\xymatrix{& (Y',y'_0)\ar[d]^{p'}\\(Y,y_0) \ar[r]_p \ar[ur]^{\tilde{p}}& (X,x_0)} \xymatrix{& (Y',y'_0)\ar[d]^{p'} \ar[ld]_{\tilde{p}'}\\(Y,y_0) \ar[r]_p&(X,x_0)}$$
Ces relevés sont des morphismes de revêtements et vérifient $\widetilde{p}\circ\widetilde{p}'(y'_0)=y'_0$ et $\widetilde{p}'\circ\widetilde{p}(y_0)=y_0$. Par conséquent, $\widetilde{p}\circ\widetilde{p}'=\mathrm{Id}$ et $\widetilde{p}'\circ\widetilde{p}=\mathrm{Id}$ et $p$ et $p'$ sont isomorphes.
Passons maintenant à la surjectivité de l’application. Soit $H$ un sous-groupe de $\pi_1(X,x_0)$. L’espace $X$ s’identifie à $\Gamma\backslash \widetilde{X}$ où $\Gamma$ agit de façon topologiquement libre. Le groupe $H$ s’identifie alors à un sous groupe $\Lambda$ de $\Gamma$ et $\Lambda\backslash \widetilde{X}\to\Gamma\backslash \widetilde{X}$ est un revêtement qui vérifie les conditions demandées.
C.Q.F.D.
Dans le cas non pointé, on obtient le théorème suivant.
L’application
$$\begin{array}{ccc}\{ \textrm{revêtements connexes}\}/\textrm{iso}&\longrightarrow &\{\textrm{ss-groupes de }\pi_1(X, x_0)\}/\textrm{conj}\\ [p : (Y, y_0) \to (X, x_0)]&\longmapsto&[H(p, x_0, y_0)]\end{array}$$
est une bijection.
Démonstration. Commençons par montrer que cette application est bien définie. Soit $p : (Y,y_0)\to (X,x_0)$ et $p': (Y',y'_0)\to (X,x_0)$ deux revêtements isomorphes.
$$\xymatrix{ (Y,y_0) \ar[dr]_{p} \ar[rr]^f&& (Y',y'_0) \ar[dl]^{p'} \\& (X,x_0) &}$$
Si $f(y_0)=y'_0$ on est dans le cadre du théorème précédent et $H(p, x_0, y_0)=H(p', x_0, y'_0)$. Il reste donc à traiter le cas $Y'=Y$ et $p'=p$. Dans ce cas $y'_0=y_0\cdot g$ où $g\in\pi_1(X,x_0)$ et $H(p, x_0, y_0\cdot g)=g\cdot H(p, x_0, y'_0)\cdot g^{-1}$.
L’application est surjective par le théorème précédent. Il reste à montrer qu’elle est injective. Considérons deux sous-groupes conjugués de $\pi_1(X,x_0)$ et $p : \Lambda \backslash \widetilde{X}\to X$ et $p' : \Lambda' \backslash \widetilde{X}\to X$ leurs revêtements associés par le théorème de classification des revêtements pointés. On a $\Lambda'=g\cdot \Lambda\cdot g^{-1}$. Alors les applications
$$\begin{array}{ccccccc} \Lambda\backslash\widetilde{X}&\longrightarrow &\Lambda'\backslash\widetilde{X'}& \mbox{ et }& \Lambda'\backslash\widetilde{X'}&\longrightarrow &\Lambda\backslash\widetilde{X}\\ \Lambda\cdot y&\longmapsto&g\Lambda\cdot y& & \Lambda'\cdot y&\longmapsto&g^{-1}\Lambda'\cdot y \end{array}$$
sont des morphismes de revêtements, inverses l’un de l’autre. Les revêtements $p : \Lambda \backslash \widetilde{X}\to X$ et $p' : \Lambda' \backslash \widetilde{X}\to X$ sont donc isomorphes.
C.Q.F.D.
Les sous-groupes de $\mathbb Z$ sont $\{0\}$ et les $n\mathbb Z$ pour $n\in\mathbb N^*$. Ainsi, les revêtements connexe du cercle sont, à isomorphisme près,
le revêtement universel
$$\begin{array}{cccc} & \mathbb R&\longrightarrow &S^1\\ &t&\longmapsto&\exp(2i\pi t) \end{array}$$
et les revêtements à $n$ feuillets
$$\begin{array}{cccc} & S^1&\longrightarrow &S^1\\ &z&\longmapsto&z^n. \end{array}$$
Revêtements galoisiens
La classification des revêtements donne naissance à une sous-classe privilégiée de revêtements, que l’on peut définir de plusieurs façons différentes, les revêtements galoisiens. On peut y penser comme les revêtements $Y \to \Gamma \backslash Y$ issus d’une action topologiquement libre, comme les revêtements « de symétrie maximale », ou comme les revêtements correspondant aux sous-groupes distingués.
Soit $p : Y \to X$ un revêtement connexe. Les assertions suivantes sont équivalentes.
- Il existe des points bases $y_0 \in Y$ et $x_0 = p(y_0) \in X$ tels que $H(p, x_0, y_0)$ soit distingué dans $\pi_1(X, x_0)$.
- Pour tout choix de points bases $y_0 \in Y$ et $x_0 = p(y_0) \in X$, le sous-groupe $H(p, x_0, y_0)$ est distingué dans $\pi_1(X, x_0)$.
- Si $y_0$ et $y'_0$ sont deux éléments de $Y$ tels que $p(y_0) = p(y'_0) = x_0$, les revêtements pointés $(Y, y_0) \to (X, x_0)$ et $(Y, y'_0) \to (X, x_0)$ sont isomorphes.
Si les assertions sont vérifiées, on dit que $p$ est un revêtement galoisien.
En particulier, le revêtement universel d’un espace connexe est galoisien. Si $p$ est galoisien, $H(p,x_0,y_0)$ ne dépend plus de $y_0$. On le note parfois $H(p)$.
Démonstration. On a vu qu’un changement de point-base correspondait à une conjugaison. La proposition précédente n’est donc rien d’autre que la traduction du fait que, si $H$ est un sous-groupe d’un groupe $G$, $H$ est distingué si et seulement si tous ses conjugués le sont, ce qui est encore équivalent à demander que tous ses conjugués coïncident.
C.Q.F.D.
Par définition, si $x_0 \in X$ est un point-base et que $F = p^{-1}\{x_0\}$ est sa fibre, le groupe des automorphismes de revêtement $\mathrm{Aut}(p)$ agit sur $F$. La dernière des trois assertions équivalentes de la proposition précédente dit donc que $p$ est galoisien si et seulement si son action sur $F$ est transitive. C’est en ce sens que l’on peut considérer les revêtements galoisiens comme les plus symétriques des revêtements connexes.
- Soit $Y$ un espace connexe et $\Gamma$ un groupe agissant topologiquement librement sur $Y$. Alors le revêtement $p :Y \to \Gamma\backslash Y$ est galoisien.
- Réciproquement, soit $p : Y \to X$ un revêtement galoisien et $G = \mathrm{Aut}(p)$. Alors l’action de $G$ sur $Y$ est topologiquement libre et $p(y) = p(y')$ si et seulement si $y$ et $y'$ appartiennent à la même orbite.
- Sous ces hypothèses, $G$ s’identifie au quotient $\pi_1(X, x_0) / H(p)$.
Soit $\widetilde{X}$ le revêtement universel d’un espace connexe $X$. Alors le groupe fondamental de $X$ s’identifie au groupe des automorphismes de $\widetilde{X}$.
Ce théorème identifie les revêtements galoisiens aux revêtements de la forme $Y \to \Gamma\backslash Y$.
Démonstration du théorème.
i. Soient $y_0$ et $y'_0$ deux points de $Y$ tels que $y'_0=g\cdot y_0$. Alors
$$\begin{array}{cccc}& Y&\longrightarrow &Y\\&y&\longmapsto&g\cdot y\end{array}$$
est un isomorphisme entre les revêtements pointés $p :(Y,y_0)\to(X,[y_0])$ et $p :(Y,y'_0)\to(X,[y_0])$. Donc $p$ est galoisien.
ii. Soit $y\in Y$, $U$ un ouvert de trivialisation de $p(y)$, $V$ une composante connexe de $p^{-1}(U)$ et $\phi\in\mathrm{Aut}(p)$ tel que $\phi(V)\cap V\neq\emptyset$. Alors, il existe $z\in V$ tel que $\phi(z)\in V$. Or $\phi$ préserve les fibres donc $\phi(z)=z$ et $\phi=\mathrm{Id}$. Si $y$ et $y'$ sont dans la même orbite alors $p(y)=p(y')$ car les automorphismes de revêtements préservent les fibres. Réciproquement, l’action de $\mathrm{Aut}(p)$ sur les fibres est transitive donc si $p(y)=p(y')$ alors $y$ et $y'$ sont dans la même orbite.
iii. Soit $p :Y\to X$ un revêtement galoisien et $y_0\in Y$. L’identification cherchée est donnée par l’application $\phi :\mathrm{Aut}(p) \to \pi_1(X, x_0) / H(p)$ vérifiant $y_0\cdot\phi(f)=f(y_0)$. L’application $\phi$ est bien définie car $H(p)$ est le stabilisateur de $y_0$ sous l’action de $\pi_1(X,x_0)$ . C’est un morphisme car
$$y_0\cdot\phi(f_1)\cdot\phi(f_2)=f_2(y_0\cdot\phi(f_1))=f_2\circ f_1(y). $$
Elle est injective car si $f\in\mathrm{Aut}(p)$ fixe un point $f=\mathrm{Id}$ et surjective car l’action sur la fibre est transitive.
C.Q.F.D.
Parmi les 7 revêtements connexes à trois feuillets du bouquet de deux cercles
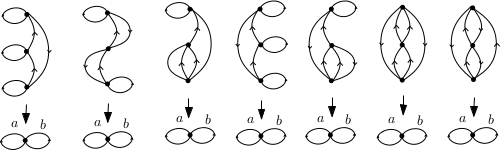
quatre sont galoisiens.
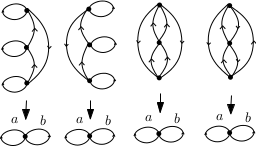
En effet, pour chacun de ces revêtements, l’action de $a$ ou de $b$ sur la fibre est un $3$-cycle. L’action du groupe fondamental de la base sur la fibre est donc transitive. Les autres revêtements ne sont pas galoisiens car les stabilisateurs des différents points d’une fibre sont différents.
On peut maintenant voir que l’action sur la fibre caractérise le revêtement et que les définitions d’espace le plus simple possible dans les théories du groupe fondamental par les lacets et les revêtements coïncident

