|
> Groupe fondamental > Groupe fondamental par les lacets > Action du groupe fondamental sur la fibre d’un revêtement Action du groupe fondamental sur la fibre d’un revêtement |
Le théorème de relèvement des homotopies permet de décrire une action du groupe fondamental sur la fibre d’un revêtement, appelée monodromie. Dans le cas d’un quotient sous l’action topologiquement libre d’un groupe $\Gamma$ cette action correspond à l’action de $\Gamma$.
Étant donné un lacet $\gamma$ basé en $x_0$, on peut définir une application $F_{x_0} \to F_{x_0}$ « de transport le long de $\gamma$ » en associant à $y_0 \in F_{x_0}$ l’extrémité de l’unique relevé de $\gamma$ issu d’un point $y_0$. En faisant varier les lacets $\gamma$, on obtient une action du groupe fondamental de $X$ sur la fibre $F_{x_0}$.
Soit $p : Y \to X$ un revêtement et $x_0 \in X$ un point-base. Soit $F_{x_0} = p^{-1}\{x_0\}$ la fibre en $x_0$ de $p$. Si $\gamma \in \Omega(X, x_0)$ est un lacet et $y_0 \in F_{x_0}$, on définit $y_0 \cdot \gamma \in F_{x_0}$ comme l’extrémité $\widetilde{\gamma}(1)$ de l’unique relevé $\widetilde{\gamma}$ de $\gamma$ tel que $\widetilde{\gamma}(0) = y_0$.
Alors $y_0 \cdot \gamma$ ne dépend que de la classe d’homotopie $[\gamma] \in \pi_1(X, x_0)$ du lacet $\gamma$ et cette construction définit une action à droite du groupe fondamental de $X$ sur la fibre $F_{x_0}$
$$ F_{x_0} \times \pi_1(X, x_0) \to F_{x_0}$$
appelée monodromie.
Le fait que l’action soit à droite signifie que, pour tout point $y$ de la fibre $F_{x_0}$, et toute paire $g,g'$ d’éléments de $\pi_1(X, x_0)$, on a
$$y \cdot (gg') = (y \cdot g) \cdot g'.$$
Cette propriété inhabituelle vient de la différence d’ordre dans les lois de groupe sur $\pi_1(X, x_0)$ et $\sigma(F_{x_0})$ : la composition $g \circ f$ des fonctions est obtenue en appliquant d’abord $f$ puis $g$ alors que la concaténation $\gamma*\gamma'$ est (à homotopie près) en suivant d’abord $\gamma$ puis $\gamma'$. L’action est donc naturellement à droite, ou, si l’on préfère, la fonction naturellement associée $\phi : \pi_1(X,x_0) \to \sigma(F_{x_0})$ est un anti-morphisme : $\phi(gg') = \phi(g') \circ \phi(g)$.
On verra dans cet article que cette action du groupe fondamental de la base sur la fibre contient essentiellement toute la structure du revêtement.
Si $X$ est le quotient d’un espace simplement connexe sous l’action topologiquement libre d’un groupe $\Gamma$, on a vu ici que $\pi_1(X,x_0)$ et $\Gamma$ sont isomorphes. Si $y_0$ est un point de la fibre de $x_0$, notre isomorphisme $\phi$ est décrit par la relation $\phi([\gamma])\cdot y_0=y_0\cdot[\gamma]$.
Les propriétés suivantes découlent directement de la définition de l’action du groupe fondamental sur la fibre.
Soit $p : (Y,y_0)\to (X,x_0)$ un revêtement connexe.
- Alors $p_*(\pi_1(Y,y_0))$ est le stabilisateur de $y_0$ sous l’action de $\pi_1(X,x_0)$.
- Soit $g\in \pi_1(X,x_0)$. Alors $p_*(\pi_1(Y,y_0\cdot g))=g\cdot p_*(\pi_1(Y,y_0))\cdot g^{-1}$.
Un revêtement est connexe par arcs si et seulement si l’action du groupe fondamental sur la fibre est transitive.
Ces propriétés permettent de retrouver le résultat suivant déjà prouvé ici : si un revêtement $p$ est connexe par arcs alors $p$ est un homéomorphisme si et seulement si $p_*$ est un isomorphisme. En effet, si $p$ est un homéomorphisme alors $p_*$ est un isomorphisme et si $p$ n’est pas un homéomorphisme, la fibre en $x_0$ contient au moins deux points distincts $y_0$ et $y_0\cdot g$. Ainsi $g$ n’est pas dans le stabilisateur de $y_0$ et $p_*$ n’est pas surjective.
Action sur la fibre et morphismes de revêtements
L’action du groupe fondamental sur la fibre se comporte également bien vis à vis des morphismes de revêtements : si $F$ est un morphisme de revêtement entre $q : (T,t_0)\to (X,x_0)$ et $p : (Y,y_0)\to (X,x_0)$
$$\xymatrix{(T,t_0)\ar[rr]^{F}\ar[rd]_{q}&& (Y,y_0)\ar[ld]^{p} \\ & (X,x_0)& }$$
et si $h\in\pi_1(X,x_0)$ alors $F(t_0\cdot h)=y_0\cdot h$.
Plus généralement, si $(F,f)$ est un morphisme de revêtements entre $q : (T,t_0)\to (Z,z_0)$ et $p : (Y,y_0)\to (X,x_0)$
$$ \begin{CD} (T,t_0) @>F>> (Y,y_0)\\ @VqVV @VpVV\\ (Z,z_0)@>f>> (X,x_0) \end{CD} $$
et si $h\in\pi_1(Z,z_0)$ alors $F(t_0\cdot h)=y_0\cdot f_*(h)$.
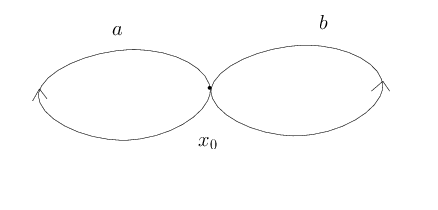
Considérons $\mathcal C$ le bouquet de deux cercles notés $a$ et $b$.
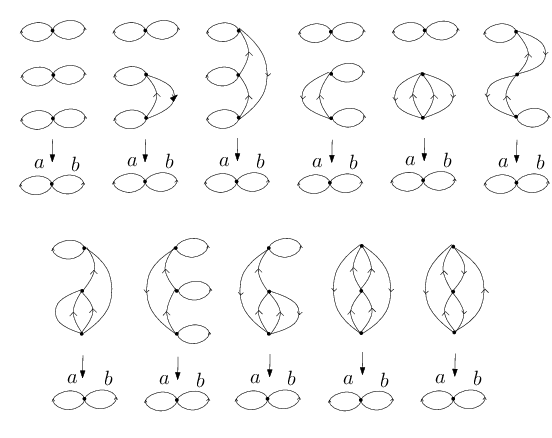
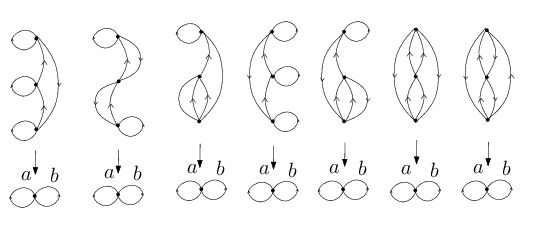
L’action du groupe fondamental $\pi_1(\mathcal C, x_0)$ sur un revêtement est déterminée par les actions de $[a]$ et $[b]$. Il y a trois permutations de l’ensemble à trois éléments à conjugaison près : l’identité, une transposition et un cycle de longueur 3. À isomorphisme près, il existe donc 11 revêtements à trois feuillets du bouquet de deux cercles.
Parmi ces revêtements, 7 sont connexes. Ils correspondent bien aux cas où l’action du groupe fondamental est transitive.
On voit ici expérimentalement que toutes les actions possibles sont réalisées par un revêtement. Cette propriété est vraie en général et expliquée dans cet article).
L’étude du groupe fondamental par les lacets se poursuit avec la construction du revêtement universel qui permet de décrire tout espace raisonnable comme un quotient.