Théorème de la boule chevelue

On se propose ici de présenter une preuve élémentaire du théorème de la boule chevelue en dimension $2$ basée sur la description du groupe fondamental de $S^1$.

Les champs de vecteurs considérés ici sont bien sûr tangents à la sphère. Une singularité correspond à un point où le vecteur nul. Il existe un énoncé plus général démontré par Brouwer en 1910 à l’aide de la théorie du degré. [1]
.

À l’inverse, il existe bien des champs de vecteurs sans singularité sur les sphères de dimension impaire. Par exemple, dans le cas du cercle, le champ $\frac{\partial}{\partial \theta}$ convient.

Démontration du théorème de la boule chevelue en dimension $2$. Supposons par l’absurde qu’il existe sur $S^2$ un champ de vecteurs $v$ sans singularité. On note alors $p_N$ et $p_S$ les projections stéréographiques de $S^2$ par rapport aux pôles nord et sud sur le plan passant par l’équateur. Grâce à $p_N$ et $p_S$, on peut transformer $v$ en des champs de vecteurs de $\mathbb R^2$, notés $v_N$ et $v_S$. En restreignant $v_N$ et $v_S$ à l’équateur, on obtient deux lacets $w_N$ et $w_S$ de $\mathbb R^2\setminus \{0\}$ ou, quitte à normaliser, deux lacets de $S^1$.

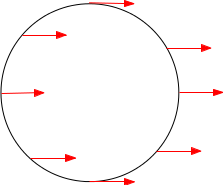
Commet $v_N$ est sans singularité sur le disque unité, le lacet $w_N$ est homotope à un lacet constant, par exemple celui-là

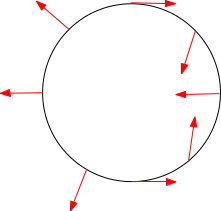
Or, $w_S$ est l’image de $w_N$ par $p_S\circ p_N^{-1}$. Donc $w_S$ est homotope à ce lacet

car $p_S\circ p_N^{-1}$ est l’identité sur $S^1$ et permute interieur et extérieur du cercle unité. Or la classe du lacet de seconde image dans $\pi_1(S^1)=\mathbb Z$ est $2$. Donc ce lacet n’est pas homotope au lacet constant. Mais $v_S$ est sans singularité dans le disque unité et donc $w_S$ est homotope au lacet constant. On obtient donc une contradiction ce qui achève la preuve du théorème.

C.Q.F.D.