|
> Groupe fondamental > Groupe fondamental par les lacets > Revêtement et relèvements Revêtement et relèvements |
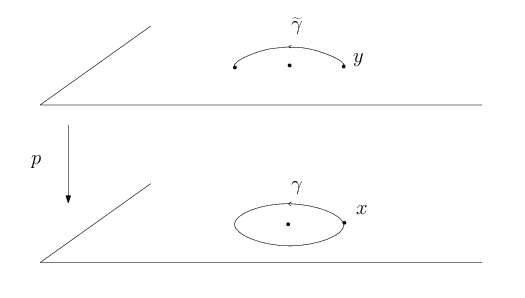
Le théorème de relèvement des chemins et des homotopies est l’ingrédient principal de l’étude des liens entre groupe fondamental et revêtement. Si $p : Y \to X$ est un revêtement $\gamma : I \to X$ un chemin de $X$, on appelle relevé de $\gamma$ tout chemin continu $\widetilde{\gamma}$ de $Y$ tel que $p \circ \widetilde\gamma = \gamma$.
Soit $p : Y \to X$ un revêtement. Soit $\gamma : I \to X$ un chemin dans $X$ issu de $x$ et soit $y \in Y$ tel que $p(y) = x$. Alors il existe un unique relevé $\widetilde\gamma : I \to Y$ de $\gamma$ tel que $\gamma(0) = y$.
La preuve de cette proposition est reportée jusqu’à la preuve d’un résultat plus général : le théorème de relèvement des homotopies.
Considérons l’exemple du revêtement
$$ \begin{array}{cccc} p:& \mathbb C^*&\longrightarrow &\mathbb C^*\\ &z&\longmapsto&z^2 \end{array} $$
L’application $\widetilde\gamma : t \mapsto e^{i\pi t}$ définit un chemin $I \to \mathbb C^*$ issu du point $y= 1$. Ce chemin est donc l’unique relevé du chemin $\gamma = p \circ \widetilde\gamma : I \to \mathbb C^*$ (qui est en fait le lacet $t \mapsto e^{2i\pi t}$) issu de $x = 1$. Choisir $y =1$ revient à choisir la détermination principale de la racine carrée sur un voisinage de $1$ : relever le chemin $\gamma$ revient à prolonger analytiquement cette détermination le long de $\gamma$. Ici, on voit que le prolongement analytique le long de $\gamma$ échange les deux détermination de la racine carrée. Il en serait de même pour tout lacet faisant un tour autour de $0$.
L’exemple illustre deux aspects importants du relèvement des chemins : tout d’abord, si $\gamma$ est un lacet, il n’y a pas de raison pour que son relevé reste fermé. Ensuite, on voit que l’extrémité $\widetilde\gamma(1)$ du relevé de $\gamma$ ne change pas lorsque l’on remplace $\gamma$ par un lacet homotope (à extrémités fixées).
Le résultat suivant est une extension du relèvement des chemins (qui correspond au cas où $K$ est un point) et permet de démontrer l’invariance par homotopie ($K = I$).
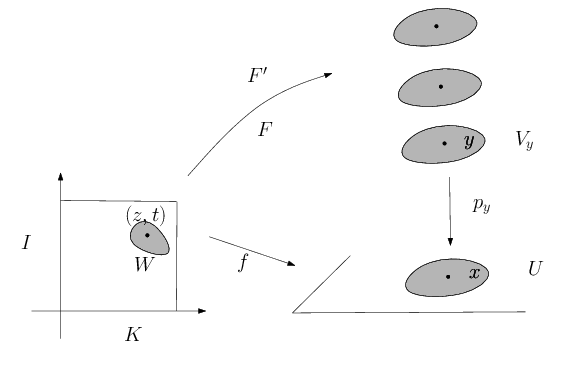
Soit $p : Y \to X$ un revêtement, $f :K\times I\to X$ une application continue et $ F_0 : K \times \{0\} \to Y$ une application relevant $f_{|K \times \{0\}}$. Alors il existe une unique application $F : K \times I \to Y$ relevant $f$ et prolongeant $ F_0$.
$$\xymatrix{&& Y\ar[d]^{p} \\ K\times I \ar[rr]_f \ar[urr]^{F} && X.}$$
Démonstration. Commençons par montrer l’unicité d’un tel relèvement. Quitte à décomposer $K$ en composantes connexes, on peut supposer que $K$ est connexe. Soient $F$ et $F'$ deux relèvements de $f$ prolongeant $F_0$.
Soit $A$ l’ensemble des points de $K\times I$ sur lesquels $F$ et $F'$ coïncident. Par continuité de $F$ et $F'$, l’ensemble $A$ est fermé. Montrons maintenant que $A$ est ouvert. Soit $(z,t)\in K\times I$. On note $x=f(z,t)$ et $y=F(z,t)$.
Soient $U$ un ouvert trivialisant du revêtement contenant $x$. On note $V_{y}$ la composante connexe de $p^{-1}(U)$ contenant $y$ et on considère l’homéomorphisme $p_y :V_y\to U$ induit par $p$. Soit $W$ un ouvert de $K\times I$ contenant $(z,t)$ tel que $F(W)\subset V_y$ et $F'(W)\subset V_y$. Comme $F$ et $F'$ relèvent $f$, il vient
$$F=p_y^{-1}\circ f \text{ et } F'=p_{y}^{-1}\circ f$$
Par conséquent $F$ et $F'$ coïncident sur $W$, ce qui prouve que $A$ est ouvert. Ainsi, $A$ est non vide, ouvert et fermé. Donc $F=F'$.
Passons maintenant à la preuve de l’existence d’un tel relèvement et commençons par prouver l’existence au voisinage de tout point de $K$. Soit donc $z_0\in K$. Par compacité de $I$, il existe
$$ t_0=0\lt t_1\lt \dots \lt t_n=1 $$
et un voisinage $N(z_0)$ de $z_0$ tels que pour tout $i\in\{1,\dots,n\}$, $f\left(N(z_0)\times[t_{i-1},t_{i}]\right)$ soit contenu dans un ouvert trivialisant du revêtement noté $U_i$.
On construit alors successivement le relevé de $f$ sur $N(z_0)\times[t_{i-1},t_{i}]$ à partir de sa valeur sur $N(z_0)\times\{t_{i-1}\}$. Soit $V_i$ la composante connexe de $p^{-1}(U_i)$ qui contient $F\left(z_0,t_{i-1}\right)$. Quitte à restreindre $N(z_0)$, on peut supposer
$$F\left(N(z_0)\times\{t_{i-1}\}\right)\subset V_i.$$
On pose alors
$$F_{N(z_0)\times[t_{i-1},t_{i}]}=p_i^{-1}\circ f$$
où $p_i: V_i\to U_i$ est l’homéomorphisme induit par $p$. Pour conclure la preuve d’existence dans le cas général, on applique le cas particulier précédent et on relève l’homotopie dans un voisinage de tout point de $K$. Par l’unicité du relèvement, deux tels relèvements coïncident sur l’intersection de leurs domaines de définition. On obtient donc un relevé bien défini sur $K\times I$.
C.Q.F.D.
Soit $\gamma_0, \gamma_1 \in \Omega(X, x_0)$ deux lacets homotopes et $\tilde\gamma_0, \tilde\gamma_1 : I \to Y$ leurs uniques relevés issus de $y_0$. Alors $\tilde\gamma_0(1) = \tilde\gamma_1(1)$.
Démonstration. Soit $\gamma_t$ une homotopie reliant $\gamma_0$ et $\gamma_1$. Par le théorème de relèvement des homotopies, on relève l’homotopie $\gamma_t$ en $\tilde{\gamma}_t $. L’extrémité libre $\tilde{\gamma}_t(1)$ définit une application continue $I \to Y$ qui vit dans l’ensemble discret $F_{x_0}$, donc elle est constante et $\tilde\gamma_0(1) = \tilde\gamma_1(1)$.
C.Q.F.D.
Le théorème de relèvement des homotopies permet de montrer des propriétés remarquables du morphisme $p_*$ induit par un revêtement $p$.
Soit $p : (Y, y_0) \to (X, x_0)$ un revêtement pointé.
- Le morphisme induit $ p_* : \pi_1(Y, y_0) \to \pi_1(X, x_0)$ est injectif.
- Si $p$ est connexe par arcs, $p$ est un homéomorphisme si et seulement si $p_*$ est un isomorphisme.
Démonstration.
- Soit $\widetilde{\gamma}\in\Omega(Y,y_0)$ tel que $p_*([\widetilde{\gamma}])=0$. Alors $\gamma=p(\widetilde{\gamma})$ est homotope au lacet constant. Le théorème de relèvement de homotopies fournit un homotopie entre $\widetilde{\gamma}$ et le relevé du lacet constant, c’est-à-dire un lacet constant. Donc $[\widetilde{\gamma}]=0$ et $p_*$ est injective.
- Si $p$ est un homéomorphisme, le résultat est immédiat. Supposons maintenant que $p$ n’est pas un homéomorphisme. Alors la fibre de $x_0$ possède au moins un élément $y_1$ distinct de $y_0$. Soit $\tilde{\gamma}$ un chemin de $Y$ reliant $y_0$ à $y_1$. L’unicité du relèvement des chemins implique $[p(\gamma)]\notin p_*(\pi_1(Y, y_0))$. Donc $p_*$ n’est pas surjective.
C.Q.F.D.
Le théorème de relèvement des chemins et des homotopies permet d’étudier les premiers exemples non triviaux de groupe fondamentaux et de définir une action du groupe fondamental de la base sur la fibre du revêtement. Cette étude est présentée dans l’article groupe fondamental d’un quotient. Ce théorème permet aussi de décrire une action du groupe fondamental sur la fibre, cette action est expliquée ici. Par ailleurs, la question de l’existence d’un relèvement est considérée pour n’importe qu’elle application continue $f : Z\to X$ dans l’article relèvement des applications.