Boucles d’oreilles hawaïennes

Les boucles d’oreilles hawaïennes (encore appelées boucles hawaïennes ou anneaux hawaïens) sont un espace topologique source de nombreux contre-exemples en topologie algébrique, et plus précisément dans la théorie du groupe fondamental. Il s’agit d’un espace topologique construit en "attachant" à un même point $z$ une infinité de cercles de rayons de plus en plus petits. Pour être plus précis, on peut par exemple les définir comme le sous-ensemble $\mathcal{H}$ [1] de $\mathbb{R}^2$ formé de la réunion des cercles de centre $(\frac{1}{2^k},0)$ et de rayon $\frac{1}{2^k}$.

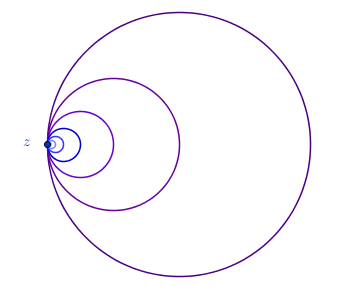
Les boucles d’oreilles hawaïennes selon les mathématicien-ne-s.

Le nom de "boucles hawaïennes" est probablement inspiré de certains bijoux comme celui que l’on voit ci-dessous. Google ne semble pas penser que ces bijoux aient quoi que ce soit d’hawaïen, mais les mathématicien-ne-s ne sont pas réputé-e-s expert-e-s en bijouterie...

Des "boucles multi-créoles" (d’après google) qui peuvent faire penser aux boucles hawaïennes des mathématiciens.

Pourquoi cet espace topologique est-t-il intéressant ?

La particularité des boucles hawaïennes, c’est que n’importe quel voisinage du point $z$ contient un petit cercle qui n’est pas homotopiquement trivial (il en contient même une infinité). C’est l’exemple le plus simple d’un espace qui n’est pas semi-localement simplement connexe. Cette propriété est source de nombreux résultats contre-intuitifs évoqués dans la vidéo suivante :

Les boucles hawaïennes ont un groupe fondamental non dénombrable

On peut définir le groupe fondamental des boucles hawaïennes comme un espace de lacets, mais contrairement à tous les autres espaces "gentils" que nous considérons sur ce site (les variétés, les $CW$-complexes), ce groupe fondamental est non-dénombrable !

Pour le montrer, nous allons construire une application injective de l’intervalle $[0,1[$ dans le groupe fondamental de $\mathcal{H}$. Soit $x \in [0,1[$ un nombre réel. Notons $x_k$ la $k$-ième décimale de $x$. On peut construire une courbe $c_x$ de classe $\mathcal{C}^1$ qui part de $z$ et parcourt $\mathcal{H}$ à vitesse constante en faisant $x_1$ fois le tour du cercle de rayon $1$, puis $x_2$ fois le tour du cercle de rayon $1/2$, puis $x_3$ fois le tour du cercle de rayon $1/4$, etc. Comme le rayon des cercles converge expontiellement vite vers $0$, cette courbe a une longueur finie et converge vers le point $z$. Elle se prolonge donc en une application du cercle dans $\mathcal{H}$ qui induit un élément $\gamma_x$ du groupe fondamental.

On peut montrer que l’application $x \mapsto \gamma_x$ est injective, ce qui montre que le groupe fondamental de $\mathcal{H}$ a au moins le même cardinal que $[0,1[$.

Les boucles hawaïennes n’ont pas de revêtement universel

On ne peut pas définir le revêtement universel des boucles hawaïennes. En effet :

Démonstration. Par définition, tout revêtement des boucles hawaïennes contient des ouverts homéomorphes à un voisinage du point $z$. Ces ouverts contiennent eux-même des lacets qui ne sont pas homotopiquement triviaux !

C.Q.F.D.

Il ne faut d’ailleurs pas confondre les boucles hawaïennes avec l’espace qu’on pourrait appeler bracelets hawaïens, obtenu en attachant en un point une infinité dénombrable de cercles "de même diamètre".

Des bracelets qui n’ont rien d’hawaïens, mais l’idée est là.

Le groupe fondamental de ces bracelets hawaïens est un groupe libre à une infinité dénombrable de générateurs. Il est donc dénombrable. Les bracelets hawaïens possèdent un revêtement universel, qui est un arbre où chaque sommet a une infinité dénombrable de voisins.

Un contre-exemple au théorème de Van Kampen fermé

Les boucles d’oreilles hawaïennes permettent de donner un contre-exemple au théorème de Van Kampen version fermée lorsqu’on ne suppose pas l’existence des ouverts de garde $U_1$ et $U_2$.

En effet, considérons l’espace $X$ formé de deux boucles d’oreilles hawaïennes $\mathcal{H}_1$ et $\mathcal{H}_2$ recollés au point $z$. La version fermée du théorème de Van Kampen prédirait que le groupe fondamental de $X$ est le produit libre des groupes fondamentaux de $\mathcal{H}_1$ et $\mathcal{H}_2$. Or il existe des éléments du groupe fondamental de $X$ qui passent une infinité de fois de $\mathcal{H}_1$ à $\mathcal{H}_2$ (en parcourant des lacets de plus en plus petits). De tels éléments ne sont pas dans le produit libre.