Commentaires sur le §VI du premier complément

Poincaré cherche à prouver dans ce paragraphe la proposition suivante. Soit $P$ une cellulation lisse d’une variété $W$ de dimension $n$.

Étant donnée la définition un peu fluctuante que Poincaré a d’une sous-variété, il est difficile d’être totalement convaincu par Poincaré ici. Le jugement de Dieudonné [1] est d’ailleurs sans appel :

Section VI of the first Complément [...] shows Poincaré at his worst, intersecting and « deforming » manifolds in the most reckless way without the slightest justification in an attempt to prove [the proposition] in the particular case [$n=3$]. (Even if the argument could be made rigorous, it would not extend to more general cases.)

On résumé ici la démonstration de Poincaré (dans le cas $n=3$ donc). L’idée générale, comme dans le paragraphe précédent, consiste à « pousser » la sous-variété $W$ dans le $(q+1)$-squelette de $P$.

Un commentaire sur la démarche.

Un énoncé similaire à celui de la proposition (et probablement un cas particulier dans l’idée de Poincaré) est que si un $q$-cycle $z$ de $P$ est le bord d’une $(q+1)$-chaîne $c$ d’une subdivision $P'$, alors il borde aussi une $(q+1)$-chaîne de $P$. Cela revient à dire que le morphisme de subdivision de $H_q(V)$ dans $H_q(V')$ est injectif. Dans les commentaires sur le §V on prouve cet énoncé en suivant la démarche de Poincaré, c’est-à-dire en poussant la chaîne $c$ dans le $q$-squelette de $V$ sans changer son bord.

$$ $$

Commençons par remarquer que si un $2$-cycle cellulaire $\sum b_j^2$ borde une sous-variété $V \subset W$, alors $V$ est nécessairement déjà cellulaire. En effet, puisque $W$ est une variété de dimension $3$, le bord ensembliste de $V$ est égal à $\sum b_j^2$ et une $3$-cellule qui contiendrait à la fois des points de $V$ et de son complémentaire devrait forcément contenir des points du bord ensembliste de $V$.

Considérons maintenant le cas d’un $1$-cycle cellulaire $\sum b_j^1$ bordant une sous-variété $V$ de dimension $2$ dans $W$. On peut supposer que $V$ est en position générale par rapport à la cellulation lisse $P$. [2] Il s’agit maintenant de modifier $V$ de manière à la rendre cellulaire.

Étant donné une $2$-cellule $a_i^2$ de $P$, on note $V(a_i^2)$ la portion de $V$ contenue dans $a_i^2$. Elle consiste en un nombre fini de sous-variétés de dimension $1$. Les cercles peuvent facilement être éliminés. [3] On peut donc supposer que $V(a_i^2)$ n’est constitué que (d’un nombre fini) d’arcs.

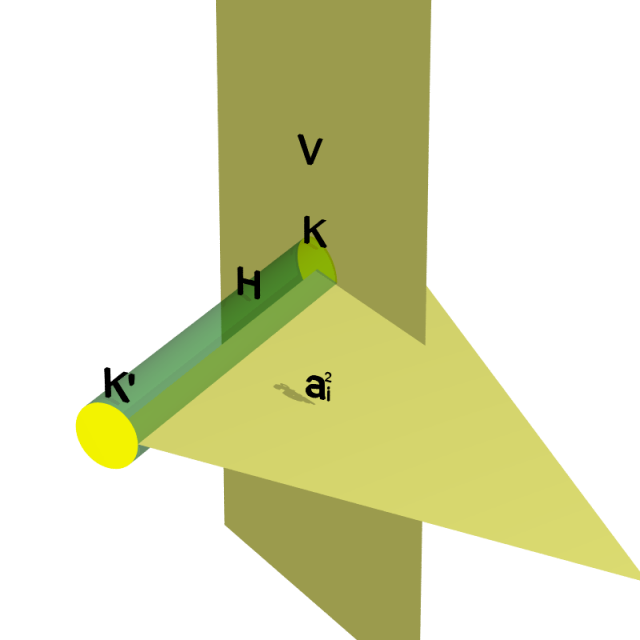
Si les extrémités de ces arcs ne sont pas contenues dans les $b_j$, alors en remplaçant $V$ par $V'=V-K+H+K'$ comme dans la figure ci-dessous on peut s’arranger pour que les extrémités en question soient toutes des sommets de la $2$-cellule.

Maintenant si la cellule $a_i^2$ contient dans son bord des arêtes $b_j$, il se peut encore que $V(a_i^2)$ soit constituée de ces $b_j$ et d’un nombre fini d’arcs intersectant le bord de $a_i^2$ selon un nombre fini de points nodaux dans l’intérieur de ces $b_j$, comme sur l’image ci-dessous.

Pour bouger un point nodal situé sur une arête $b_j$ de $a_i^2$ vers un sommet de celle-ci on procède de la manière suivante. On commence par tracer dans $V$ un arc $L$ proche de $b_j$ mais ne le rencontrant qu’en ses extrémités. Soit alors $S_1$ un portion de surface obtenu en « balayant » cet arc jusqu’à un arc similaire $L'$ contenu dans une autre $2$-cellule adjacente à $a_i^2$ le long de $b_j$. Remplacer $V$ par $V'=V-V_1+S_1+S_1'$ a pour effet de supprimer le point nodal de $a_i^2$ ou de le repousser jusqu’à un sommet. C’est ce que montre l’animation ci-dessous où l’on a colorié en jaune la portion de surface $V$, en vert les $2$-cellules $a_j^2$, en bleu les courbes $L$ et en orange la surface $S_1$ puis la nouvelle surface $V'$.

Le point nodal est bien supprimé : s’il existait un point nodal de $a_i^2$ sur $b_j$ on pourrait tracer un arc dans $V' (a_i^2)$ aboutissant en ce point nodal. Mais cela est impossible puisqu’un tel arc finirait par pénétrer la région $S_1 '$ qui ne rencontre $a_i^2$ que le long de $b_j$. [4]

La nouvelle $V$ découpe chaque $2$-cellule selon des arcs $L$ dont les extrémités sont des sommets de $P$. Pour pousser un tel arc dans le bord de la $2$-cellule correspondante, on choisit une $2$-cellule $Q \subset a_i^2$ dont le bord est la réunion de $L$ et d’un arc $L'$ contenu dans le bord de $a_i^2$ et de mêmes extrémités que $L$. [5] On peut ensuite effacer une petite bande « verticale » de $V$ passant par $L$ et la remplacer par deux cellules comme $Q$ mais situées « au-dessus » et « en-dessous » de $Q$ ainsi qu’une nouvelle bande verticale passant par $L'$.

On obtient finalement une nouvelle sous-variété $V$ telle que chaque portion $V(a_i^3)$ de $V$ dans une $3$-cellule borde un $1$-cycle constitué d’arêtes de cette $3$-cellule. On remplace maintenant $V(a_i^3)$ par une $2$-chaîne de $\partial a_i^3$ de même bord. [6] En faisant cela pour toutes les $3$-cellules on est finalement ramené au cas désiré où la sous-variété $V$ est cellulaire.

C.Q.F.D.