Commentaires sur le §XI du premier complément

Les résultats du premier complément sont relatifs à une variété (différentielle) qui admet une décomposition cellulaire. Il n’est pas difficile de vérifier qu’une variété admet telle décomposition si et seulement si elle peut être triangulée. Dans ce paragraphe Poincaré s’intéresse au problème plus profond de l’existence d’une triangulation. Il tente de démontrer le théorème suivant.

Esquissons la tentative de démonstration de Poincaré. Il raisonne par récurrence sur la dimension $p$. On suppose donc le théorème démontré en dimension $< p$.

Poincaré suppose que la variété $V$ connexe est définie comme réunion de variétés $v$ chacune étant paramétrée par une sous-variété de dimension $p$ dans $\mathbb{R}^q$ définie par $q-p$ équations. À l’aide du théorème des fonctions implicites, il ramène cette définition à la définition moderne où $V$ est définie comme la réunion de variétés $v'$ chacune étant paramétrée par $\mathbb{R}^p$.

Alors, dans chaque $v'$, il définit le sous-ensemble $v''$ constitué des points qui ne sont contenus dans aucune autre sous-variété $v'$. Poincaré dit alors :

il est clair qu’on peut s’arranger de telle façon que tout point de $V$ appartienne à l’une des variétés $v''$, et à une seule, à moins qu’il ne soit sur la frontière de l’une des variétés $v''$

Autrement dit, les $v''$ formeraient un recouvrement de $V$ par des sous-variétés d’intérieurs disjoints. C’est pourtant loin d’être « clair » : ainsi définis les $v''$ ne vérifient certainement pas cette propriété. Il faut opérer des modifications sur les parties communes à plus de trois variétés $v'$, mais Poincaré ne dit rien de ce qu’il faut faire.

Supposons pourtant dorénavant que les $v''$ sont bien définies. Il reste encore du travail puisque les $v''$ ne sont pas nécessairement des cellules, ni même simplement connexes.

Dans chaque $v''$ paramétrée par $p$ variables $z_1 , \ldots , z_p$, Poincaré choisit une origine et considère les (demi-)rayons :

$$z_1 = t \alpha_1 , \ldots , z_p = t \alpha_p \quad (t>0).$$

Il suppose implicitement que ces rayons intersectent $\partial v''$ en un nombre fini de points. [1]

Il s’en suit que, à l’exclusion des rayons remarquables tangents en certains points de $\partial v''$, tous les rayons intersectent $\partial v''$ en un nombre impair de points. Le cône remarquable, constitué des rayons remarquables, intersecte $\partial v''$ selon une sous-variété $U$ de dimension $\leq p-2$ qui divise $\partial v''$ en régions.

Soit $R\subset \partial v''$ une des régions introduites au paragraphe précédent. La région $R$ est de première sorte si un (et donc tout) rayon quitte $v''$ depuis $R$. Dans le cas contraire la région est dite de seconde sorte.

Ces régions sont de dimension $p-1$. L’hypothèse de récurrence permet donc en particulier de trianguler toutes celles de ces régions qui sont de première sorte. Poincaré étend alors cette triangulation en une subdivision de $v''$ en cônes, ou plutôt sections de cônes sur des $(p-1)$-simplexes à partir de l’origine, obtenus comme réunion des rayons passant un simplexe de la triangulation des régions de première sorte. On peut finalement subdiviser en $p$-simplexes les sections de cônes ainsi obtenus. Tout ceci est illustré dans la figure ci-dessous où l’on représente les rayons remarquables en bleu, les autres rayon en vert, les sections de cônes en vert clair et où l’arête jaune est ajoutée pour subdiviser une section de cône en deux triangles.

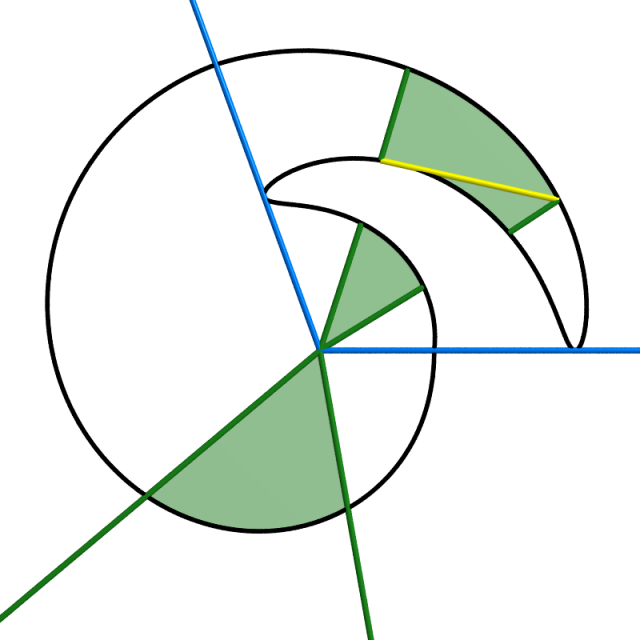
Toutefois « une difficulté subsiste » : les triangulations induites du bord de deux $v''$ différentes ne coïncident pas en général. Pour surmonter cette difficulté, Poincaré considère une subdivision simpliciale commune aux différentes triangulations de tous les $\partial v''$. Si $T$ est un tétraèdre de dimension $p$ entre deux régions $R$ (de première sorte) $T$ s’obtient comme la « jonction » (join en anglais) $T_1 * T_2$ de deux tétraèdres $T_1$ et $T_2$ contenus dans les deux régions $R$. La subdivision commune aux différentes triangulations de tous les $\partial v''$ induit des subdivisions des simplexes $T_1$ et $T_2$. Et la jonction de ces subdivisions fournit la triangulation recherchée.

Si, à la suite de cette « démonstration » Poincaré est

débarrassé des derniers doutes

son lecteur lui ne l’est peut-être pas tout à fait. Il faut en tout cas attendre Whitehead pour que la communauté mathématique soit véritablement débarrassé des derniers doutes quand à la possibilité de trianguler les variétés différentielles. On consacre une rubrique au théorème de Whitehead.